2.6. Расстояние от точки до прямой

Пусть задана прямая

L: Ах+Вy+С=0

и точка

Определить расстояние от точки до прямой L.

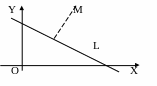
Кратчайшее расстояние между точкой и прямой L – это перпендикуляр, опущенный из этой точки на прямую, т.е.

(2.9)

2.7. Взаимное расположение двух прямых на плоскости

1. Условие параллельности и перпендикулярности прямых.

а) Прямые параллельны, если их угловые коэффициенты равны, т.е.

где - угловой коэффициент первой прямой,

- угловой коэффициент второй прямой.

Пример 5.

Прямые у=5х-3,

у=5х+6

являются параллельными.

б) Прямые перпендикулярны, если для их угловых коэффициентов выполняется соотношение:

.

Пример 6.

Прямые у=2х+8

у= х+3

являются перпендикулярными.

2. Точка пересечения двух прямых.

Точка пересечения двух прямых лежит одновременно на каждой из этих прямых. Поэтому координаты ее должны удовлетворять уравнениям обеих прямых.

Отыскание этих координат выполняется совместным решением системы уравнений этих прямых, т.е.

- точка пересечения прямых и .

3. Угол между двумя прямыми.

Пусть даны прямые

Угол между ними определяется по формуле:

(2.10)

Пример 7.

Найти угол между прямыми 5x-12y-16=0 и 3x+4y-12=0.

Решение.

Если прямые заданы в виде прямых с угловыми коэффициентами т.е.:

то угол между и находится по формуле:

2.8. Линии второго порядка

Уравнения таких линий в прямоугольной системе координат являются уравнениями второй степени. Такие линии называются линиями второго порядка.

а) Окружность – есть множество всех точек плоскости, расстояние каждой из которых от одной точки плоскости, называемой центром, есть величина постоянная.

Пусть - центр окружности; r – ее радиус; - произвольная точка окружности. Тогда уравнение вида

(2.11) называется нормальным уравнением окружности.

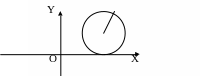
Если a=b=0 , то имеем окружность с центром в начале координат.

X

Если раскрыть скобки уравнения (1) и ввести новые обозначения

A=-2a; B=-2b;

то

(2.12) Уравнение (2.12) называется общим уравнением окружности.

Пример 8.

Определить координаты центра и радиус окружности

Решение.

Здесь А=0; В=6; С=-7.

Найдем координаты центра следующим образом:

а) А=-2а; -2а=0; а=0;

б) В=-2b; 6=-2b; b=-3;

в) r=4.

Ответ: координаты центра М(0;-3); радиус r=4.

б) Эллипс – есть множество всех точек плоскости, для которых сумма расстояний от двух данных точек и , называемых фокусами, есть величина постоянная, обозначенная 2а.

- называется фокусным расстоянием.

=2с.

По определению

(2.13)

Используя формулы расстояний между точками и М; и М и соотношение (2.13), уравнение эллипса можно записать в следующем виде:

(2.14) Уравнение (2.14) называется каноническим (простейшим) уравнением эллипса, где

а – большая полуось эллипса;

b – малая полуось эллипса;

с – фокусное расстояние.

Отношение фокусного расстояния с к большой (или малой) оси эллипса а (b) называют эксцентриситетом. Обозначается (эпсилон).

; .

Различают следующие случаи:

если a>b, (т.е. эллипс вытянут по оси ОХ), то

если a<b, (т.е. эллипс вытянут по оси OY), то

Пример 9.

Найти длины осей эллипса вычислить координаты его фокусов и эксцентриситет.

Решение.

1. Исходное уравнение приведем к каноническому виду:

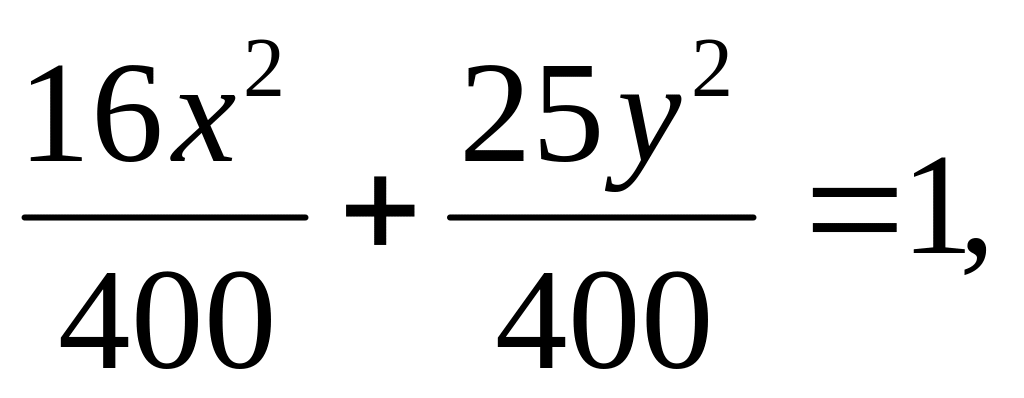
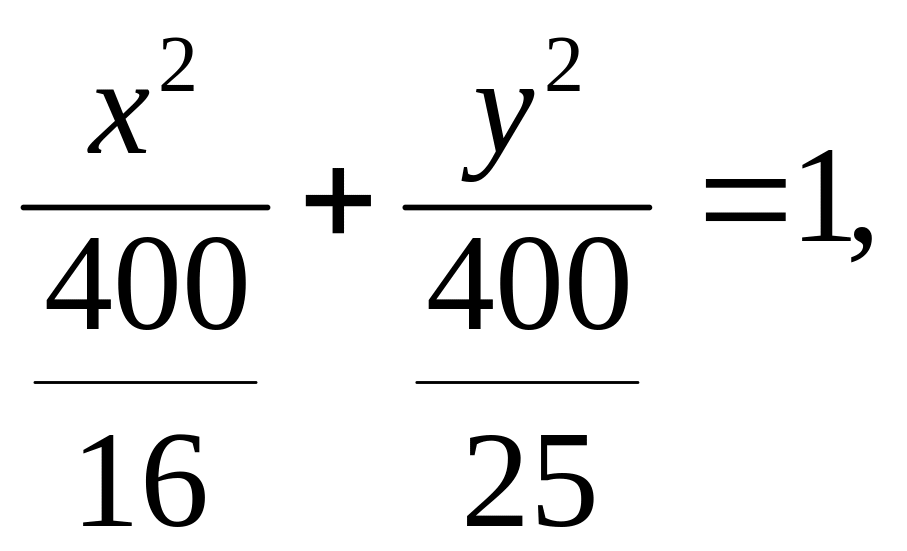
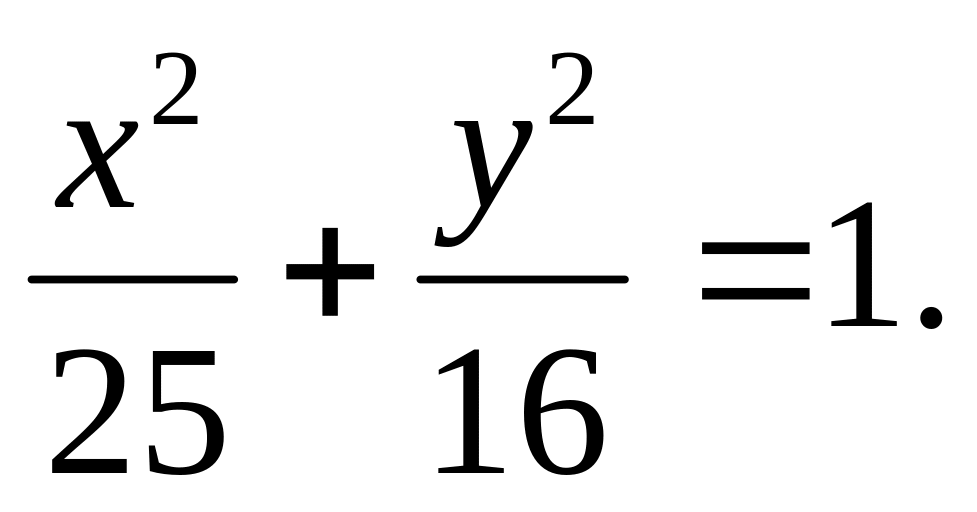
2. Отсюда

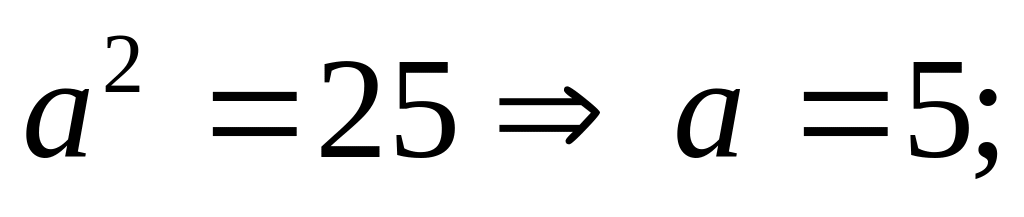
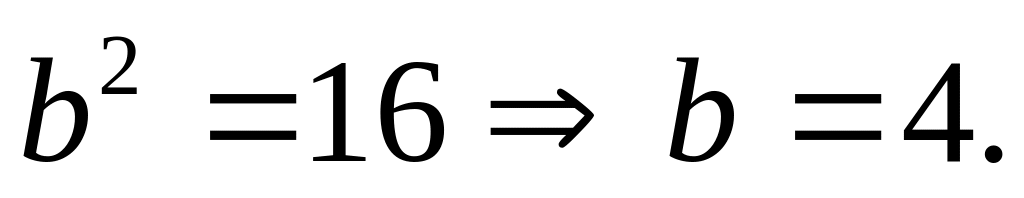
3. Длина осей эллипса: 2а=10, 2b=8.

4. Случай 1) a>b, следовательно .

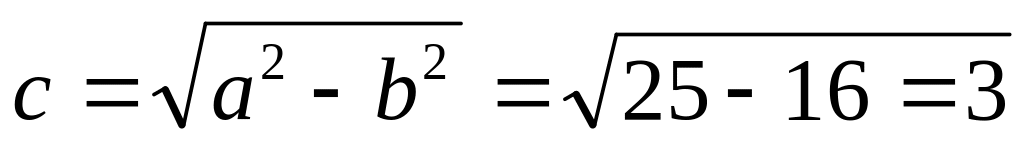5. Эксцентриситет:

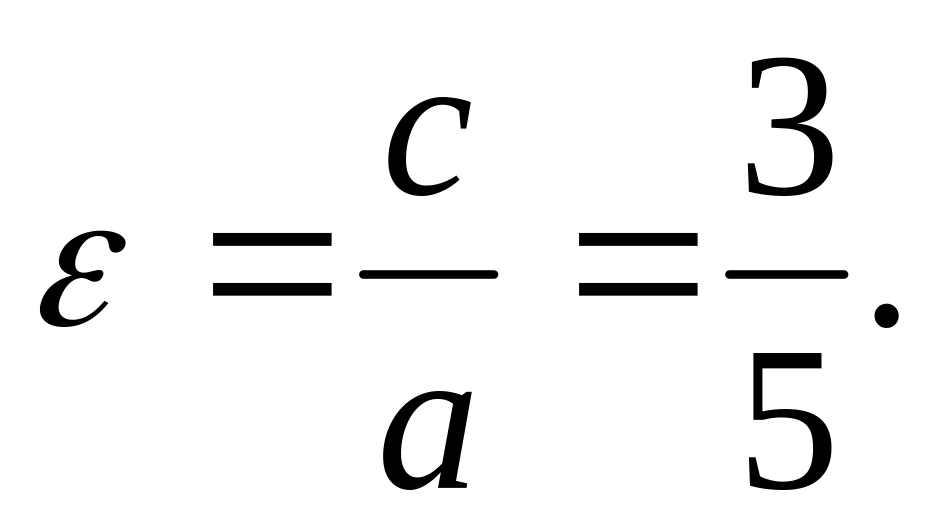
Ответ:

в) Гипербола.

Гиперболой называется множество всех точек плоскости для которых разность расстояний и от двух постоянных точек и , являющихся фокусами, есть величина постоянная, равная 2а.

а, b – полуоси гиперболы, - координаты фокусов.

(2.15) Уравнение (2.15) называется каноническим уравнением гиперболы.

Вершины гиперболы – это координаты точек пересечения гиперболы с осью абсцисс. Это точки

- полуфокусное расстояние.

Отношение - называется эксцентриситетом гиперболы.

Уравнения асимптот и гиперболы.

Пример 10.

Дана гипербола Определить длину ее осей и расстояние между фокусами.

Решение.

Имеем:

2а – действительная ось, равная 6;

2b – мнимая ось, равная 10.

Расстояние между фокусами найдем следующим образом:

=

г) Парабола.

Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом F, и от данной прямой, называемой директрисой. Обязательное условие: директриса не должна проходить через фокус.

F – фокус,

прямая k – директриса, где р – параметр параболы;

r=d – по определению;

p – расстояние от фокуса до директрисы;

d – расстояние от (.)М до директрисы;

r – расстояние от (.)М до фокуса.

(2.16) уравнение (2.16) называется каноническим уравнением параболы.

Исследование параболы.

а) уравнение

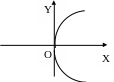
б) уравнение

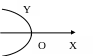
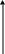
в) уравнение

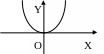
г) уравнение

Y

O X

Пример 11.

Парабола с вершиной в точке О(0;0) проходит через (.)М (8;4).Симметрична относительно оси ОХ. Написать уравнение параболы.

Решение.

Каноническое уравнение параболы т.к. (.)М лежит на параболе, то ее координаты должны удовлетворять уравнению параболы., т.е - есть уравнение данной параболы.