2.4. Деление направленного отрезка в заданном отношении

Y

O X

Пусть направленный отрезок, а (.)М – любая точка оси, на которой лежит отрезок . (.)М может лежать и внутри отрезка, и вне его. Будем говорить, что она делит направленный отрезок . При этом, если (.)М[AB], то делит его внутренним образом, а если (.)М[AB], внешним образом.

Число называется отношением, в котором (.)М делит отрезок .

Если М[AB], то 0,

если М[AB], то 0.

Отношение, в котором (.)М делит отрезок (=) есть , которое можно выразить через абсциссы точек (.)А, (.)М, (.)В.



(2.2)

Таким же образом находим через ординаты точек (.)А, (.)М, (.)В.

(2.3)

2.5. Линии первого порядка

а) Общее уравнение прямой – это уравнение вида

Ах+Ву+С=0, (2.4) где А, В, С некоторые коэффициенты, т.е. числа R.

Л юбая прямая описывается уравнением (1) при соответствующем выборе коэффициентов А, В, С. Уравнение (1) является неполным, если какой- либо из коэффициентов равен нулю.

1. С=0, при А>0, В>0 имеем

Ах+Ву=0; у=-

уравнение прямой, проходящей

через начало координат.

2. В=0; А0; С0

и

Y

O X X

меем Ах+С=0;

х=- ;

прямая, параллельная оси Оу.

3. В0; А=0; С0.

В у+С=0; у=- .

Прямая,

параллельная оси Ох.

б) Уравнение прямой с угловым коэффициентом.

Это уравнение может быть получено из общего уравнения прямой.

Ах+Ву+С=0;

Ву=-Ах-С;

у=-

где к=- - угловой коэффициент, b=- - некоторое действительное число, равное величине отрезка, отсекаемого прямой на оси ординат.

Таким образом

y=kx+b, (2.5)

k=tg, где - угол наклона прямой к оси Ох.

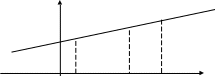
Пример 3.

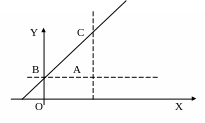
Построить прямую, заданную уравнением y= .

k= , b=3, отрезок СА=2, отрезок ВА=3, отношение ОВ=3.

в) Уравнение прямой в отрезках.

Общее уравнение прямой Ах+Ву+С=0.

Пусть А0; В0; С0;

Ах+Ву=-С

разделим обе части на –С

Перепишем иначе

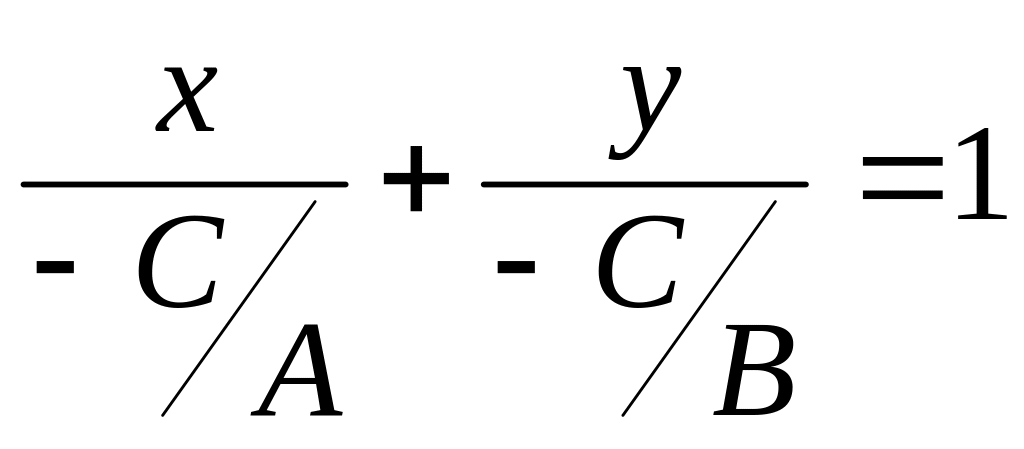
обозначим:

; ;

имеем:

(2.6)

Это уравнение прямой в отрезках. Числа a и b – это величины отрезков, которые прямая отсекает на осях координат. (Эта форма удобна для геометрического построения прямой.)

Пример 4.

Прямая задана уравнением: 2х+8у+4=0. Составить для этой прямой уравнение в отрезках и построить ее.

Решение.

2х+8у+4=0   

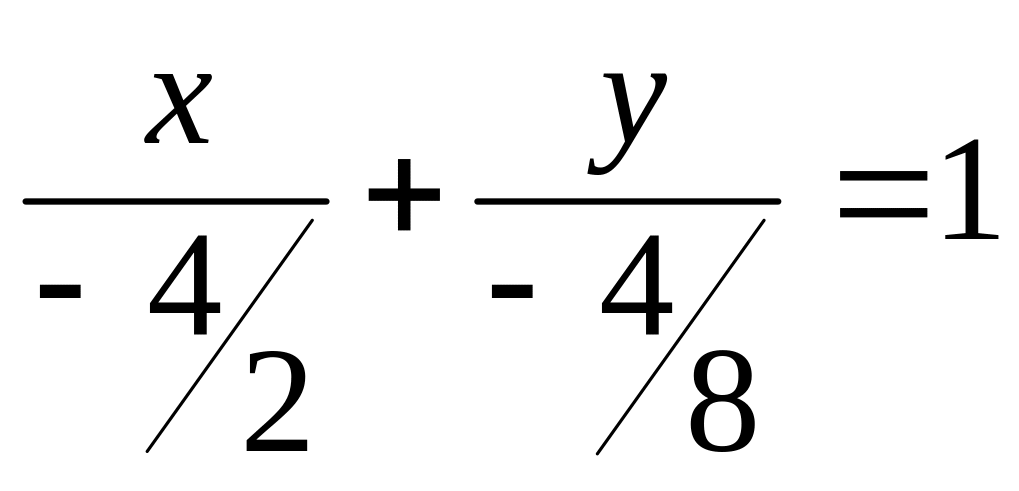
г) Уравнение прямой, проходящей через две данные точки.

Пусть даны две точки и , и пусть - любая точка искомой прямой. Тогда выражение

(2.7)

называется уравнением прямой, проходящей через две данные точки.

Пример 5.

Даны точки А(5;4) и В(-3;2). Составить уравнение прямой, проходящей через точки А и В.

Решение.

Пусть ; ; ; .

д) Уравнение прямой с угловым коэффициентом.

Рассмотрим уравнение прямой, проходящей через две заданные точки

Если его записать

и обозначить , то уравнение прямой, имеющей угловой коэффициент k и проходящей через точку , имеет вид

(2.8) Уравнение (2) называют так же уравнением пучка прямых с центром в точке