
- •Математика
- •Глава 1 элементы теории множеств
- •1.1 Понятие множества.
- •1.2. Элемент и принадлежность элемента к множеству. Операции над множествами
- •1.3. Действительные числа
- •Отрезок, интервал, окрестность
- •Глава 2 начала аналитической геометрии
- •2.1. Метод координат
- •Прямоугольная система координат на плоскости
- •2.2. Уравнение линии на плоскости
- •2.3. Расстояние между двумя точками на плоскости
- •2.4. Деление направленного отрезка в заданном отношении
- •2.5. Линии первого порядка
- •2.6. Расстояние от точки до прямой
- •2.7. Взаимное расположение двух прямых на плоскости
- •2.8. Линии второго порядка
- •2.9. Решение задач
- •Глава 3. Введение в анализ. Пределы
- •3.1. Понятие функции. График функции
- •3.2. Элементарные функции и их графики
- •3.3. Предел числовой последовательности
- •3.4. Предел функции
- •3.5. Бесконечно малые и бесконечно большие величины
- •3.6. Основные теоремы о пределах
- •3.7 Вычисление пределов
- •3.8. Непрерывность функции. Точки разрыва
- •3.9. Решение задач
- •Глава 4. Дифференциальное исчисление.
- •4.1. Понятие производной.
- •4.2. Геометрический смысл производной.
- •4.4. Основные формулы дифференцирования.
- •4.5. Дифференциал функции.
- •Приближенные вычисления с помощью дифференциала.
- •4.6. Решение задач
- •Продифференцировать следующие функции
- •Глава 5. Элементы интегрального исчисления.
- •5.1. Определение интегрирования.
- •5.2. Неопределенный интеграл.
- •5.3. Таблица простейших интегралов.
- •5.4. Непосредственное интегрирование
- •5.5. Методы интегрирования
- •Метод основан на использовании формулы дифференцирования произведения двух функций. Пусть u и V дифференцируемые функции от х. Тогда
- •Глава 6. Элементы теории вероятностей
- •6.1. Предмет теории вероятностей
- •6.2. Классическое определение вероятности
- •6.3. Теоремы сложения и умножения вероятностей
- •6.4. Формула полной вероятности
- •6.5. Формулы Байеса
- •6.6.Схема Бернулли
- •6.7. Закон распределения и числовые характеристики дискретной случайной величины
- •6.8. Решение задач
2.1. Метод координат
Определение
1: отрезок, на котором указано направление
(т.е. указано, какая из двух граничных
точек считается началом, например А, а
какая – концом, например В), называется
направленным отрезком и обозначается
![]() .
.
Определение 2: прямая, на которой выбрано положительное направление и единица масштаба, называется осью.
Определение
3: величиной направленного отрезка
,
расположенного на оси, называется его
длина
![]() ,
взятая со знаком (+), если направление
отрезка совпадает с положительным
направлением оси , и со знаком (-) в
противоположном случае.
,
взятая со знаком (+), если направление
отрезка совпадает с положительным
направлением оси , и со знаком (-) в
противоположном случае.
Замечание: длина – это положительная величина, полученная путем измерения этого отрезка с помощью другого, заранее выбранного отрезка, играющего роль единицы масштаба.
Нулевой отрезок – длина равна нулю, а направление не определено.
Определение 4: если на прямой выбрано:
Начало отсчета – точка (.) О;
Положительное направление;
Единица масштаба,
тогда мы говорим, что на этой прямой установлена система координат.
Обозначим
Р(х), любую точку Р с координатой х.
Зададим две точки А(![]() )
и В(
)
и В(![]() ).
Тогда
).
Тогда
длина
![]()
т.е. расстояние между двумя точками равно абсолютной величине разности координат этих точек.
Прямоугольная система координат на плоскости
Возьмем две взаимно перпендикулярные оси.

ОХ
– ось абсцисс ОY
– ось ординат
Для
любой (.) М ее положение на плоскости
YОХ
определяется двумя числами
![]() и обратно.
и обратно.
Любые два числа определяют некоторую точку на плоскости YOX, т.е.
определяют
(.) М![]() ,
где
-
двумерное пространство действительных
чисел, а
,
где
-
двумерное пространство действительных
чисел, а
![]() -
проекции точки М на оси OХ и ОY.
Таким образом положение любой точки на
плоскости полностью описывается
проекциями этой точки на координатные
оси. При этом абсциссой точки М
называется величина направленного
отрезка
-
проекции точки М на оси OХ и ОY.
Таким образом положение любой точки на
плоскости полностью описывается
проекциями этой точки на координатные
оси. При этом абсциссой точки М
называется величина направленного
отрезка
![]() ,
началом которого является (.) О, а концом
(.) М. Ординатой (.) М называется
величина направленного отрезка
,
началом которого является (.) О, а концом
(.) М. Ординатой (.) М называется
величина направленного отрезка
![]() , началом которого является (.) О, а
концом (.)
, началом которого является (.) О, а
концом (.)
![]() .
.
Оси координат делят плоскость на четыре части, называемыми квадрантами (четвертями, координатными углами).
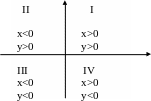
Это декартова (1637 г.) или прямоугольная система координат. (.) М задается координатами М(х,У).
2.2. Уравнение линии на плоскости
В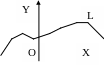 озьмем
на плоскости какую-нибудь линию L,
выберем в этой плоскости декартову
систему координат и рассмотрим
произвольную точку М линии L.
озьмем
на плоскости какую-нибудь линию L,
выберем в этой плоскости декартову
систему координат и рассмотрим
произвольную точку М линии L.

Если перемещать точку М по линии L, то ее координаты будут изменяться, оставаясь связанными некоторым условием, характеризующим точки линии. Это соотношение в общем виде записывается
F(x,y)=0 (*) где F означает символ функции двух переменных, т.е. линии на плоскости соответствует некоторое уравнение с двумя переменными х и y.
Примеры уравнений (линий):
2x+5y+3=0,
![]() ,
,
![]() …
и
т.д.
…
и
т.д.
2.3. Расстояние между двумя точками на плоскости
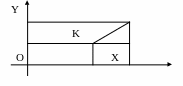
Пусть
заданы (.) А(![]() и (.) В
и (.) В![]() ,
и пусть АВ
,
и пусть АВ
![]() и
и
![]() .
.
![]()
![]()
![]()
![]()
АК
║
![]() .
Обозначим
.
Обозначим
![]() .
.
Тогда по теореме Пифагора
![]()
или
![]() (2.1)
(2.1)
