6.4. Формула полной вероятности

Пусть событие А может произойти только с одним из событий (гипотез) , образующих полную группу событий. Тогда вероятность события А вычисляется по формуле полной вероятности:

Или

Пример 13. На конвейер поступают однотипные детали, изготовленные на 3-х станках. На первом станке изготовлено 25%, на втором – 35%, на третьем – 40% всех деталей. В их продукции брак составляет соответственно 15%, 12% и 6%. Найти вероятность того, что наудачу взятая с конвейера деталь бракованная.

Решение. Пусть

А={наудачу взятая с конвейера деталь бракованная}.

Гипотезы

={деталь изготовлена на 1-м станке},

={деталь изготовлена на 2-м станке},

={деталь изготовлена на 3-м станке}.

События образуют полную группу попарно несовместных событий.

Условные вероятности

Тогда

6.5. Формулы Байеса

Формулы Байеса позволяют переоценить вероятности гипотез, принятых до испытания, по результатам уже проведенного испытания.

Пример 14._{Имеется две равные партии деталей, причем известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии четверть деталей недоброкачественные. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что вторая деталь из этой же партии окажется недоброкачественной, если первая деталь после проверки возвращена в партию.}

_{Решение. Пусть событие А состоит в том, что первая деталь оказалась доброкачественной. Введем гипотезы: Н1 – взята партия с недоброкачественными деталями, Н2 – взята партия доброкачественных деталей. По условию задачи , , . Поэтому по формуле полной вероятности вероятность события А будет .}

_{После первого извлечения вероятность того, что партия содержит недоброкачествнные детали , по формуле Байеса равна:}

_.

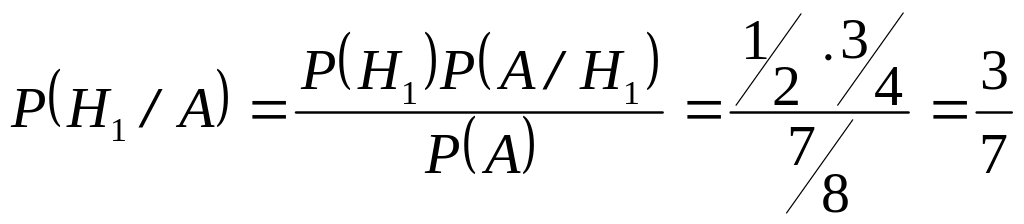_{Вероятность того, что партия содержит только доброкачественные детали находится аналогично:}

_.

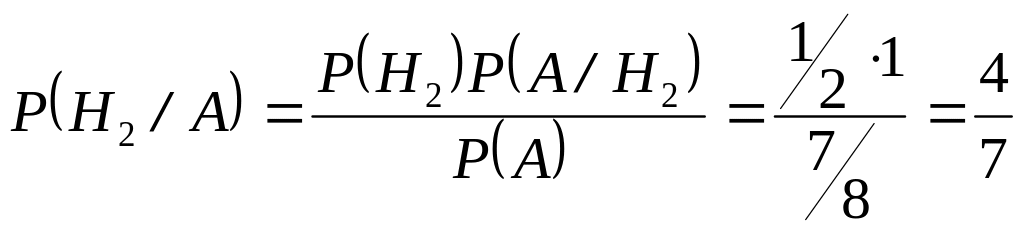_{Пусть событие В заключается в том, что при втором извлечении деталь оказалась недоброкачественной. Вероятность данного события также находится по формуле полной вероятности.}

_{Если и – вероятности гипотез и после первого извлечения и установления факта, что деталь доброкачественная, то согласно предыдущим вычислениям , . Кроме того, , . Поэтому искомая вероятность}

_.

6.6.Схема Бернулли

_{Вероятностные задачи, связанные с многократным повторением испытаний, постоянно встречаются в практике. Например, в финансовой области это покупка и продажа акций, ценных бумаг, валюты и т.д.; в социологии – опросы и тестирование; в управлении производством – процессы контроля качества.}

_{В таких задачах необходимо вычислять вероятность появления интересующего нас события заданное число раз при многократном повторении испытания.}

_{Определение. Последовательность независимых n испытаний с двумя исходами (А – «успех», - «неудача») и постоян6ной вероятностью «успеха» p (Р=Р(А)) в каждом испытании называется схемой Бернулли.}

_{В схеме Бернулли вычисляют: вероятность того, что в n последовательных независимых испытаниях будет ровно k «успехов».}

_{- формула Бернулли,}

_{где - количество испытаний,}

_{k – количество «успехов» в n испытаниях (k=0, 1,…,n),}

_{p+q=1 , p – вероятность «успеха», q – вероятность «неудачи».}

_{Возможны следующие варианты использования формулы Бернулли. Если нас интересует, что «успех» появится:}

1. _{менее k раз, то}

_.

2. _{более k раз, то}

_.

3. _{не менее k раз, то}

_,

4. _{не более k раз, то}

_,

5. _{хотя бы один раз}

_.

_{Каждая вероятность, входящая в формулы (1) – (5) вычисляется по формуле Бернулли.}

_{Пример 15.}

_{Всхожесть семян данного растения имеет вероятность 0,8. Какова вероятность того, что из 5 посеянных семян взойдет не менее 4?}

_{Решение.}

_{Можно считать, что имеется n=5 испытаний Бернулли с вероятностью успеха p=0?8 и неуспеха q=0?2. По формуле Бернулли находим:}

_.

_{Тогда искомая вероятность равна}