Глава 6. Элементы теории вероятностей

6.1. Предмет теории вероятностей

В практической деятельности мы часто встречаемся с явлениями, которые мы наблюдаем, но результат которых нельзя предсказать, так как он зависит от случая.

Пример 1: через два дня выпадет снег, В Ленинском районе города Новосибирска 15 декабря 2002 года будет 20 автомобильных происшествий, учетная ставка ЦБ 25 апреля 2003 года будет 20% и т.д.

Таким образом наблюдаемые явления можно разделить на 3 вида: достоверные, невозможные случайные.

Достоверным называется событие, которое обязательно происходит.

Невозможным называется событие, которое заведомо не произойдет.

Случайным называется событие, которое может произойти, а может и не произойти.

Установлением закономерностей поведения случайных событий и занимается теория вероятностей. Причем для установления закономерностей должны быть данные о массе случайных событий (множестве случайных событий) однородных (т.е. многократное наблюдение за погодой, многократное подбрасывание монеты,…).

Испытание (опыт) – выполнение какого-либо действия, связанного с наблюдением какого-либо явления, которое происходит в одних и тех же условиях.

Событие – результат испытания, т.е. всякий факт, который в результате опыта может произойти или не произойти. События (или исходы опыта) обозначаются заглавными латинскими буквами A,B,C,… .

Совокупность всех взаимоисключающих друг друга исходов испытания образуют пространство элементарных событий (исходов) Ω. Элементарные события обозначают ω.

С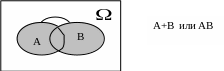 умма

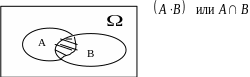
Пересечение

Р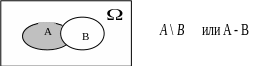 азность

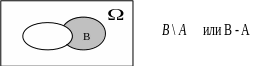
А

 - пустое множество.

Противоположное

с обытие

В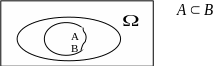 ключение

Операции над событиями:

Пример 2:

Для исследования состава семей в городе Н. из всех семей с тремя детьми выбрана одна. Рассматриваются следующие события:

А={первый ребенок – мальчик, последняя – девочка};

В={второй ребенок – мальчик};

С={в семье есть мальчик и девочка}.

Требуется:

1) описать пространство элементарных исходов и события

2) Проверить попарную несовместность событий А, В, С.

3) Проверить, образуют ли события А, В, С полную группу.

Решение:

1) Испытание – проверка состава семьи и возраста ребенка. Обозначим: М – появление (рождение) мальчика, Д – появление (рождение) девочки. В семье, состоящей из трех детей, возможны следующие исходы:

={МММ, ММД, МДМ, МДД, ДММ, ДМД, ДДМ, ДДД}, т.е. элементарный исход - любая комбинация мальчиков и девоче6к из трех детей данной семьи. .

Событие А= событие

событие событие

событие событие

- события А и В совместны;

- события В и совместны;

2)События называются попарно несовместными, если любые два события из этой совокупности являются несовместными. Так как , то то события А, В, С совместны.

3) События образуют полную группу событий, если они: а) попарно несовместны; б) хотя бы одно из событий происходит (т.е. А+В+С= ).

Так как оба условия не выполняются, то события А, В, С не образуют полной группы.