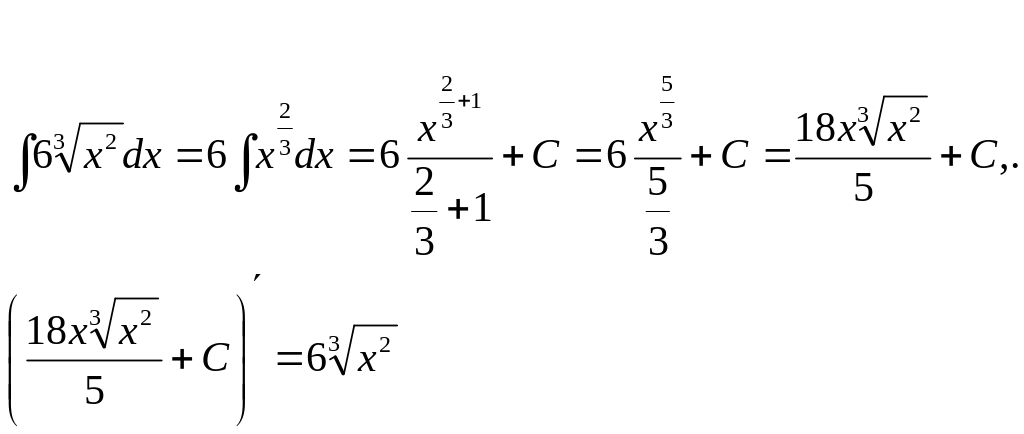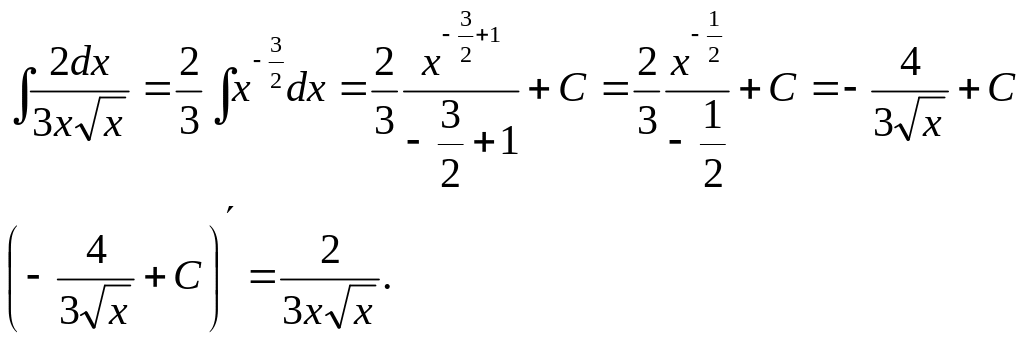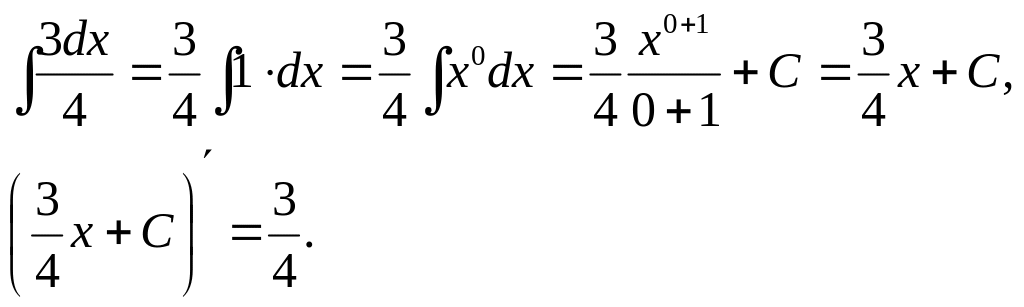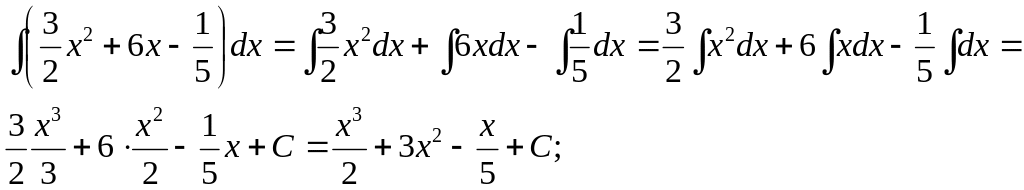5.3. Таблица простейших интегралов.
Справедливость формул интегрирования проверяется дифференцированием.
Пример 1.
Проверить дифференцированием правильность интегрирования:
Решение.
Пример 2.
Найти интегралы и результаты проверить дифференцированием:
5.4. Непосредственное интегрирование
Пример 3.
Найти интегралы.
5.5. Методы интегрирования
Интегрирование при помощи замены переменного (метод подстановки).
Путем введения новой переменной часто удается упростить подынтегральное выражение и тем самым облегчить интегрирование. Такой прием называется методом подстановки.
Пример 4.
Найти
интеграл
Решение.
Введением
новой переменной приведем интеграл к
виду
Для этого аргумент подынтегральной
функции обозначим через новую переменную
t:
.
Найдем дифференциал получившейся
функции:
Откуда
Теперь переходим под знаком интеграла к новой переменной t, вычисляем получившийся интеграл и, затем, возвращаемся к старой переменной х.
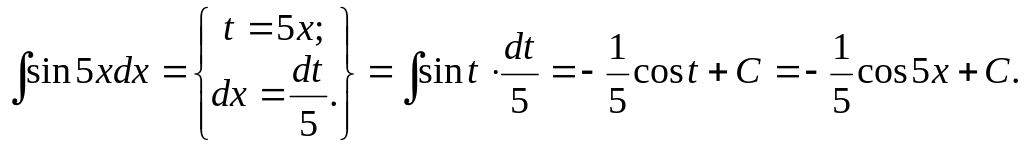
Интегрирование по частям.
Метод основан на использовании формулы дифференцирования произведения двух функций. Пусть u и V дифференцируемые функции от х. Тогда
Откуда
Проинтегрируем обе части этого выражения
или
.
Это
формула интегрирования по частям. Она
позволяет переходить от заданного
интеграла
к другому интегралу
,
который может быть проще.
Формула используется тогда, когда интеграл не решается предыдущими методами, или когда подынтегральная функция является: логарифмической, обратной тригонометрической, показательной и некоторыми другими функциями.
Пример 5.
Пример 6.
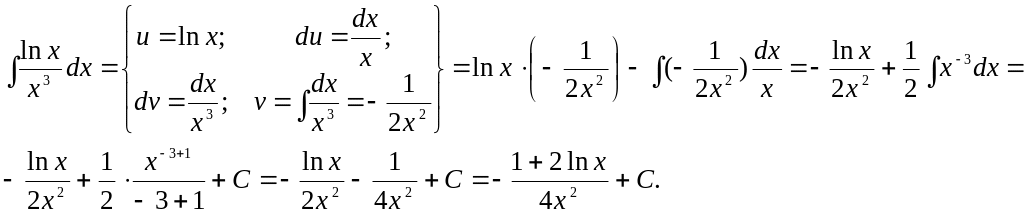
Интегрирование рациональных функций.
Рациональной функцией
называется дробь
,
в которой числитель
и знаменатель
многочлены.
Правильной дробью называется дробь, у которой наивысшая степень многочлена числителя меньше наивысшей степени многочлена знаменателя.
Пример 7.
-
правильные рациональные дроби.
Неправильной дробью называется дробь, у которой наивысшая степень многочлена числителя больше или равна наивысшей степени многочлена знаменателя.
Пример 8.
неправильные
дроби.
При интегрировании неправильных дробей нужно выделить целую часть, разделив многочлены (по правилу деления многочленов), и остаток.
Пример 9.
Записать неправильную дробь в виде целой части и остатка.:
Пример 10.
Найти интеграл:
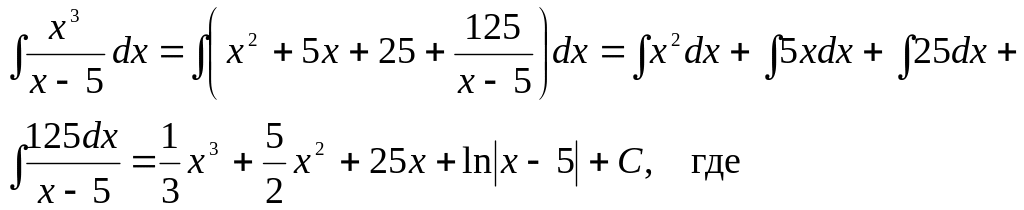
Интегралы от функций, содержащих квадратный трехчлен.
Для отыскания указанных интегралов следует вначале выделить полный квадрат из квадратного трехчлена, в результате чего он преобразуется в квадратный двучлен.
Пример 11.
Найти интеграл:
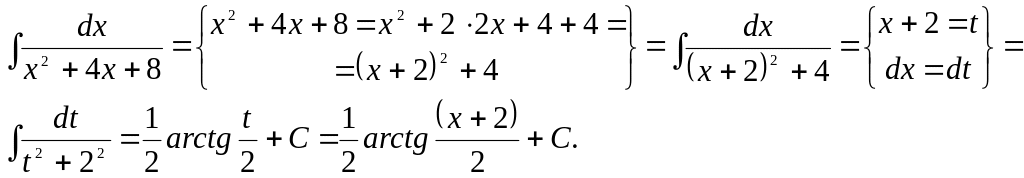
5.6. Определенный интеграл. Его свойства
Определенным интегралом называют интеграл вида
a – нижний предел интегрирования,
b – верхний предел интегрирования.
Для того, чтобы вычислить определенный интеграл, нужно:
1)найти
соответствующий неопределенный интеграл
;
2)подставить в полученное выражение сначала верхний предел интегрирования b, затем нижний предел интегрирования a;
3)из первого результата вычесть второй.
Иначе
Свойства определенного интеграла:
-
при перестановке предела интегрирования
меняется знак;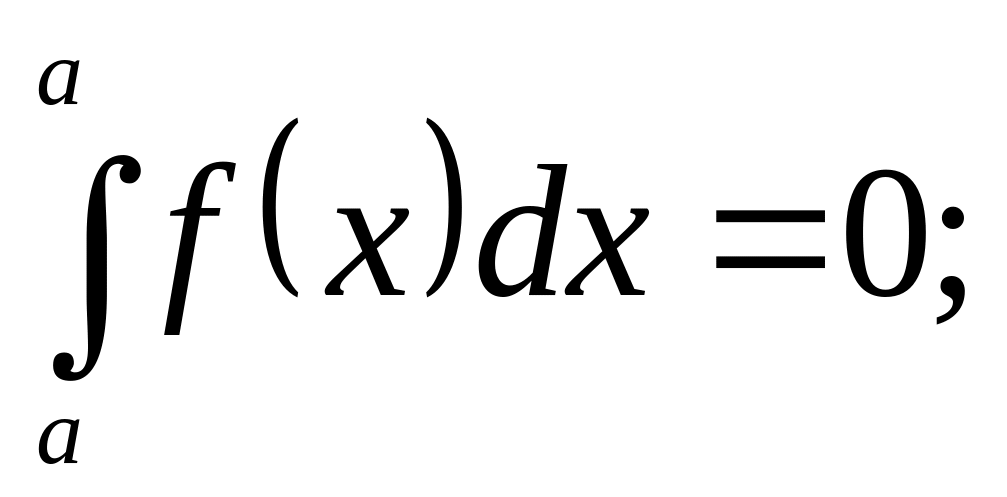
-
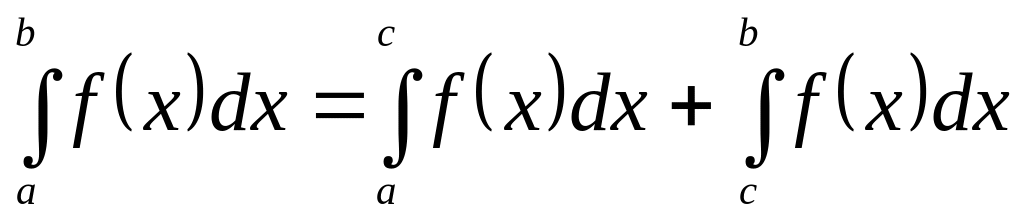отрезок интегрирования можно разбивать
на части;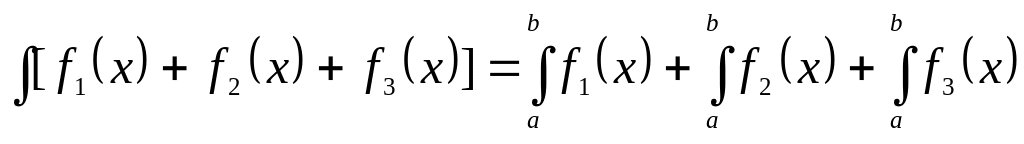
-
интеграл от суммы функций равен сумме
интегралов от всех слагаемых;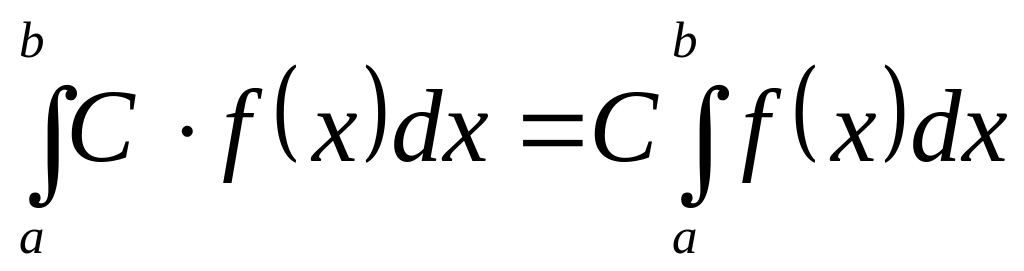
-
постоянный множитель можно выносить
за знак интеграла.
Пример 12.
Вычислить определенный интеграл:
5.7. Метод замены переменных в определенном интеграле
Правило: при замене в определенном интеграле старой переменной интегрирования на новую необходимо старые пределы интегрирования заменить новыми.
Пример 13.
Найти определенный интеграл:
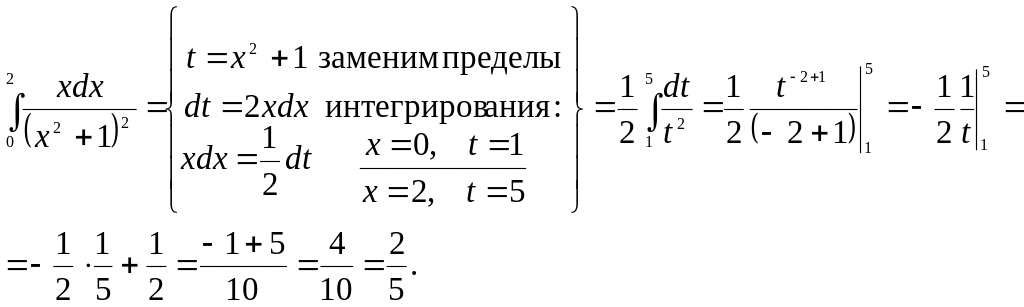
5.8. Вычисление площадей с помощью определенного интеграла
Правило.
Площадь криволинейной трапеции,
ограниченной кривой
,
осью абсцисс и двумя вертикальными
прямыми х=а и х=b, вычисляется
по формуле:
Пример 14.
Найти площадь фигуры, ограниченной линиями:
Решение:
Сделаем чертеж.
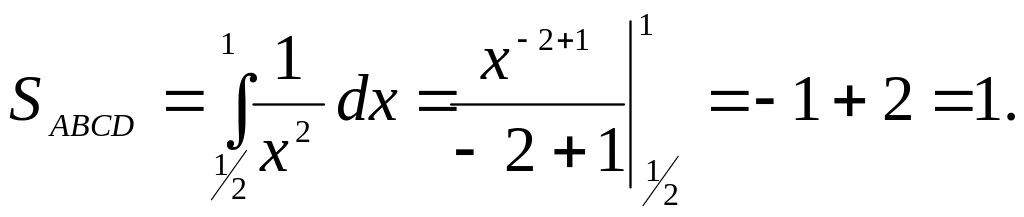
5.9. Решение задач
Задача 1.
Найти интегралы:
а)
б)
Задача 2.
Найти интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
Задача 3.
Найти интегралы:
а)
б)
в)
г)
Задача 4.
Найти интеграл:
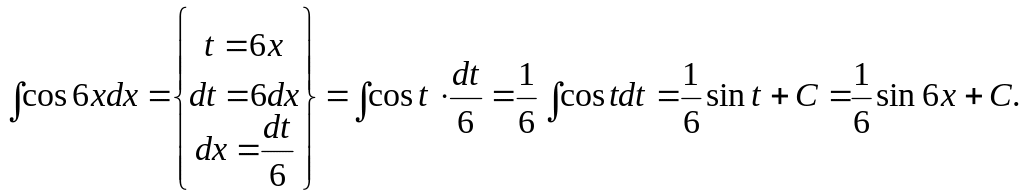
Задача 5.
Найти интеграл:
Задача 6.
Найти интеграл:
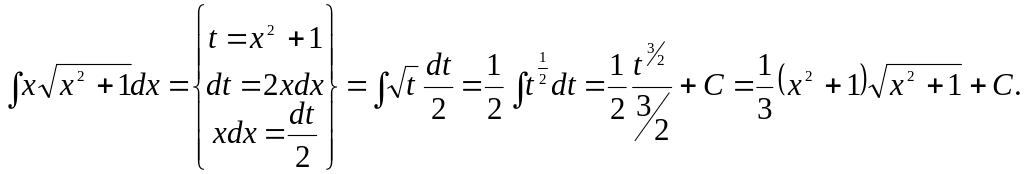
Задача 7.
Найти интеграл:
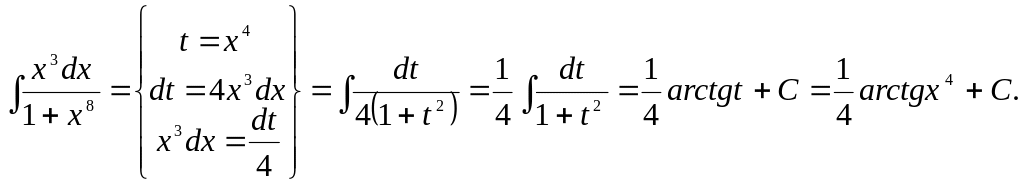
Задача 8.
Найти интеграл:
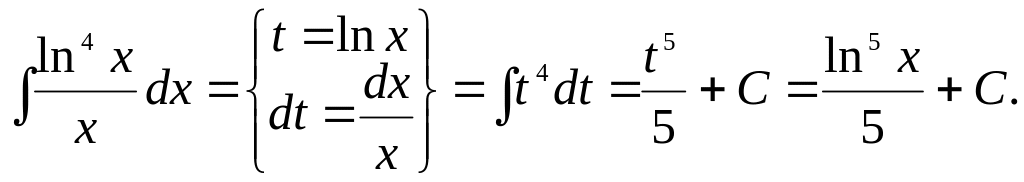
Задача 9.
Найти интеграл:
Задача 10.
Найти интеграл:
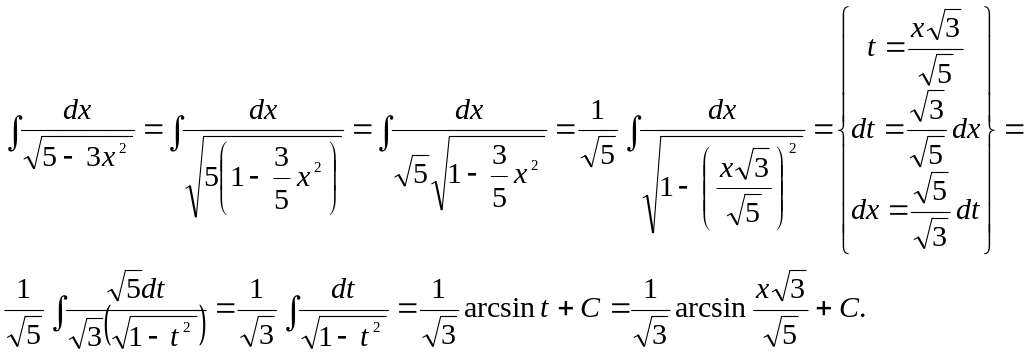
Задача 11.
Найти интеграл:
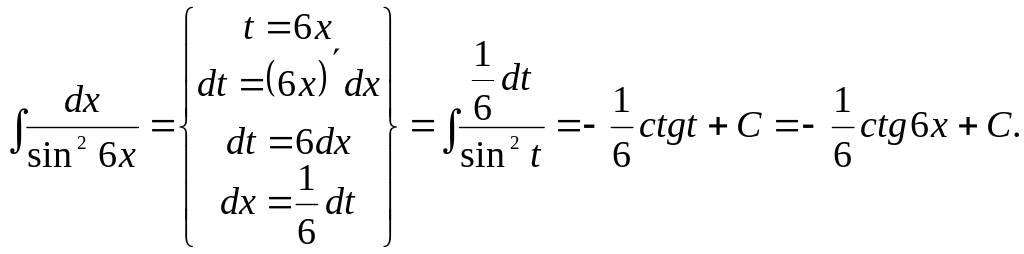
Задача 12.
Найти интеграл:
Задача 13.
Найти интеграл:
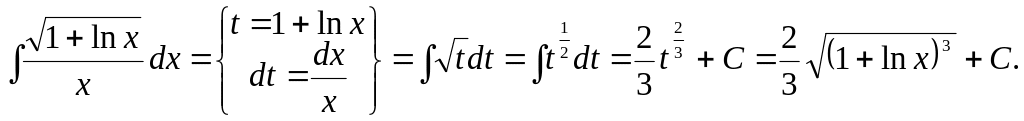
Задача 14.
Найти интегралы:
а)
Ответ:
б)
Ответ:
в)
Ответ:
Задача 15.
Найти интеграл:
Задача 16.
Найти интеграл:
Задача 17.
Найти интегралы:
а)
Ответ:
б)
Ответ:
Задача 18.
Найти интеграл:
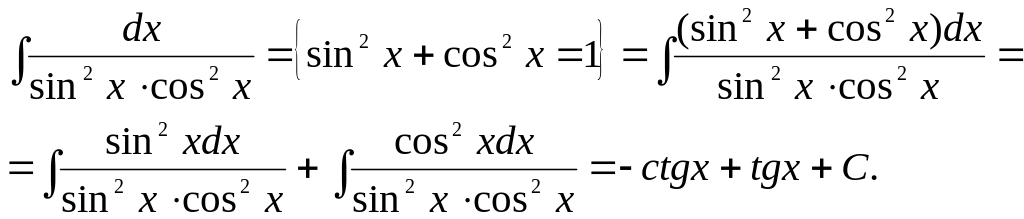
Задача 19.
Найти интеграл:
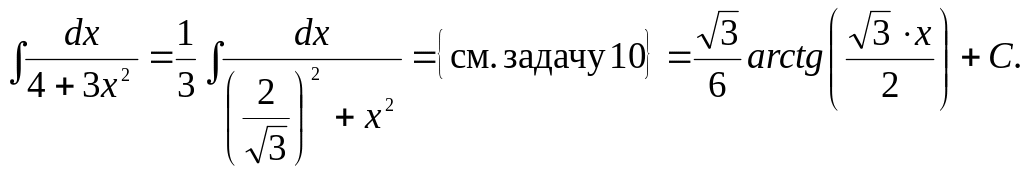
Задача 20.
Найти интегралы:
а)
Ответ:
б)
Ответ:
в)
Ответ:
г)
Ответ:
д)
Ответ:
е)
Ответ:
ж)
Ответ:
Задача 21.
Найти интеграл:
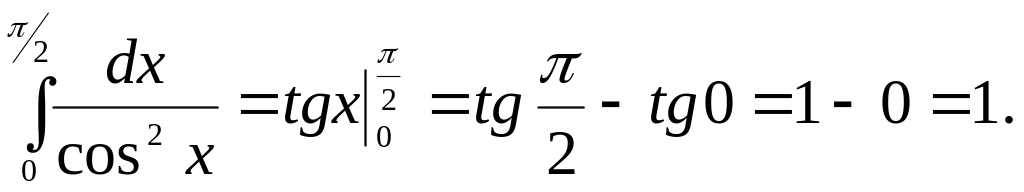
Задача 22.
Найти интеграл:
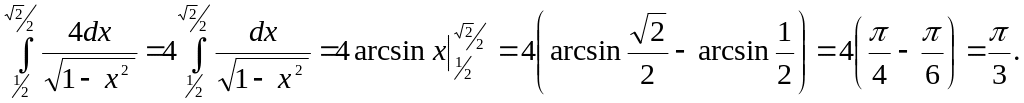
Задача 23.
Найти интеграл:
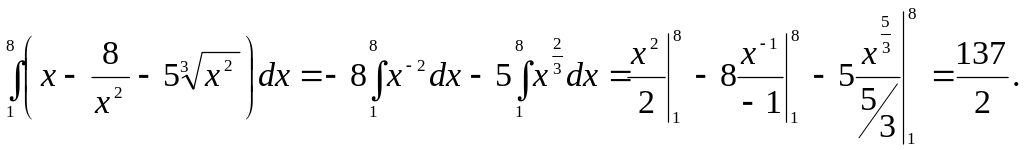
Задача 24.
Найти интегралы:
а)
Ответ:
б)
Ответ:
в)
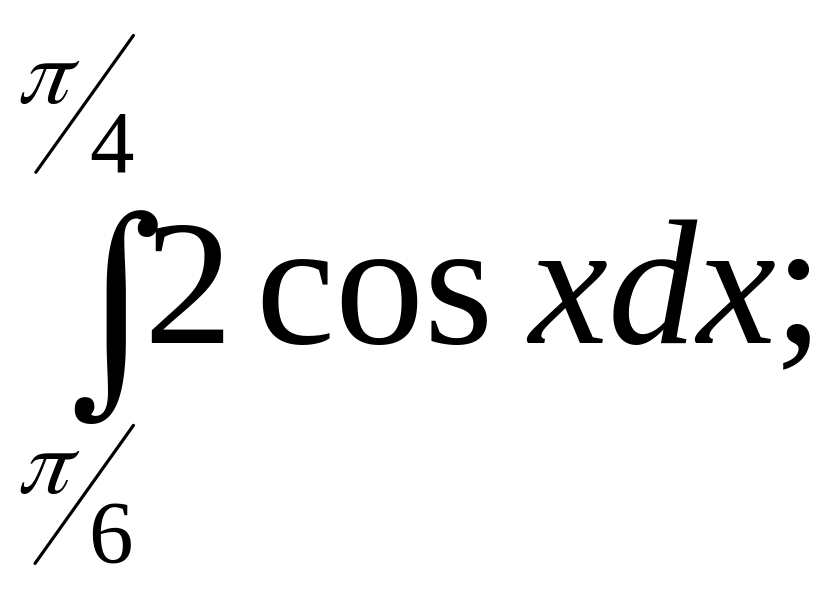Ответ:
г)
Ответ:
д)
Ответ: 91,2.
Задача 25.
Найти интеграл:
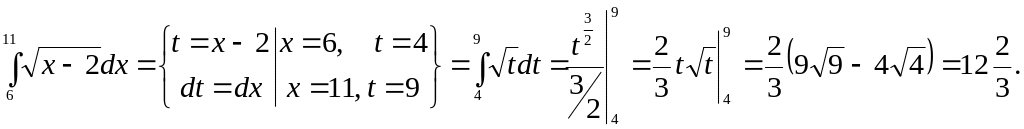Задача
26.
Найти интеграл:
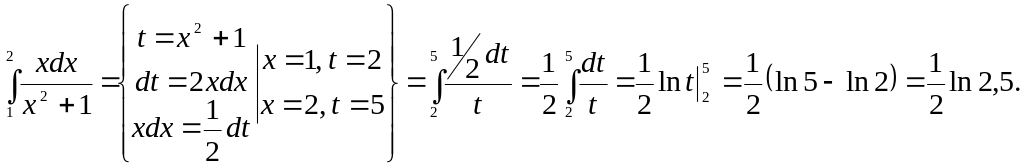
Задача 27.
Найти интеграл:
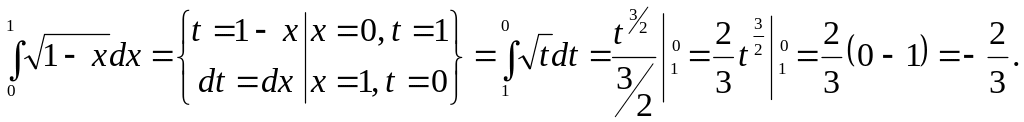
Задача 28.
Найти интегралы:
а)
Ответ:
б)
Ответ: 4.
В)
Ответ:
Задача 29.
Найти
площадь фигуры, ограниченной линиями:
параболой
прямыми х=1, х=4 и осью Ох. Ответ:
Задача 30.
Найти
площадь фигуры, ограниченной линиями:
параболой
и прямой у=х+3.
Решение:
Решая совместно данные уравнения, определим точки пересечения параболы и прямой:
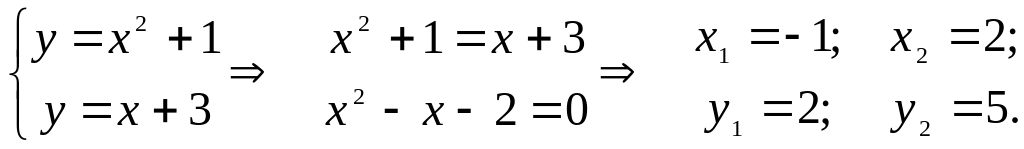
А(2;5), В(-1;2) – точки пересечения данных линий.
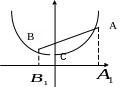
Искомую
площадь S можно получить
как разность площадей трапеции
и криволинейной трапеции
.
Задача 31.
Найти
площадь фигуры, ограниченной линиями:
параболой
и прямой
