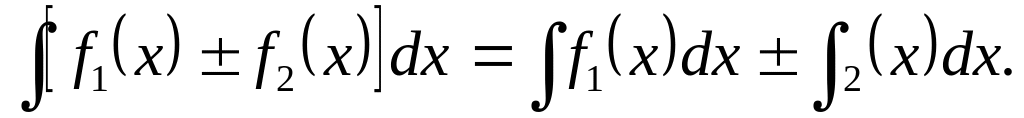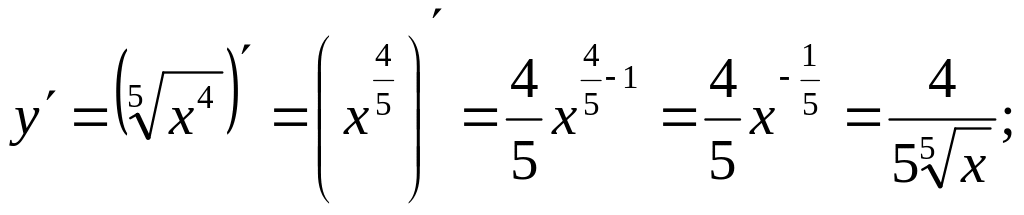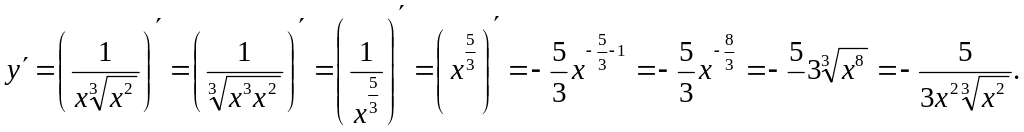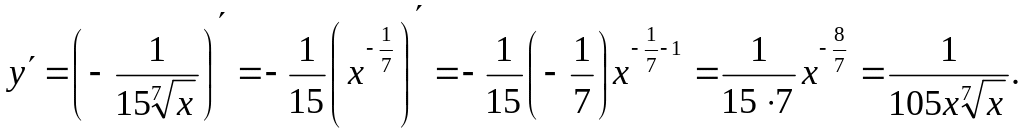- •Математика
- •Глава 1 элементы теории множеств
- •1.1 Понятие множества.
- •1.2. Элемент и принадлежность элемента к множеству. Операции над множествами
- •1.3. Действительные числа
- •Отрезок, интервал, окрестность
- •Глава 2 начала аналитической геометрии
- •2.1. Метод координат
- •Прямоугольная система координат на плоскости
- •2.2. Уравнение линии на плоскости
- •2.3. Расстояние между двумя точками на плоскости
- •2.4. Деление направленного отрезка в заданном отношении
- •2.5. Линии первого порядка
- •2.6. Расстояние от точки до прямой
- •2.7. Взаимное расположение двух прямых на плоскости
- •2.8. Линии второго порядка
- •2.9. Решение задач
- •Глава 3. Введение в анализ. Пределы
- •3.1. Понятие функции. График функции
- •3.2. Элементарные функции и их графики
- •3.3. Предел числовой последовательности
- •3.4. Предел функции
- •3.5. Бесконечно малые и бесконечно большие величины
- •3.6. Основные теоремы о пределах
- •3.7 Вычисление пределов
- •3.8. Непрерывность функции. Точки разрыва
- •3.9. Решение задач
- •Глава 4. Дифференциальное исчисление.
- •4.1. Понятие производной.
- •4.2. Геометрический смысл производной.
- •4.4. Основные формулы дифференцирования.
- •4.5. Дифференциал функции.
- •Приближенные вычисления с помощью дифференциала.
- •4.6. Решение задач
- •Продифференцировать следующие функции
- •Глава 5. Элементы интегрального исчисления.
- •5.1. Определение интегрирования.
- •5.2. Неопределенный интеграл.
- •5.3. Таблица простейших интегралов.
- •5.4. Непосредственное интегрирование
- •5.5. Методы интегрирования
- •Метод основан на использовании формулы дифференцирования произведения двух функций. Пусть u и V дифференцируемые функции от х. Тогда
- •Глава 6. Элементы теории вероятностей
- •6.1. Предмет теории вероятностей
- •6.2. Классическое определение вероятности
- •6.3. Теоремы сложения и умножения вероятностей
- •6.4. Формула полной вероятности
- •6.5. Формулы Байеса
- •6.6.Схема Бернулли
- •6.7. Закон распределения и числовые характеристики дискретной случайной величины
- •6.8. Решение задач
4.6. Решение задач
Задача 1.
Вычислением
найти производную функции
![]() .
.
Задача 2.
Продифференцировать следующие функции
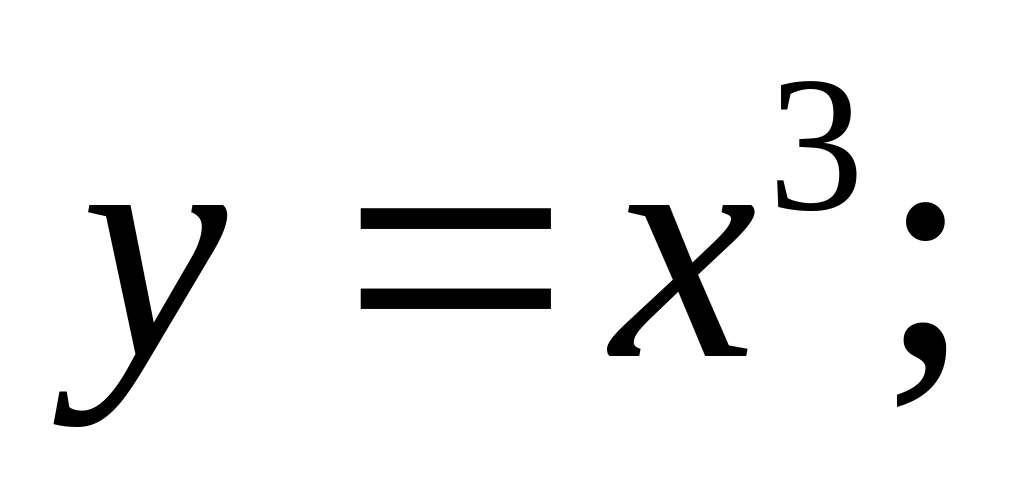 2)
2)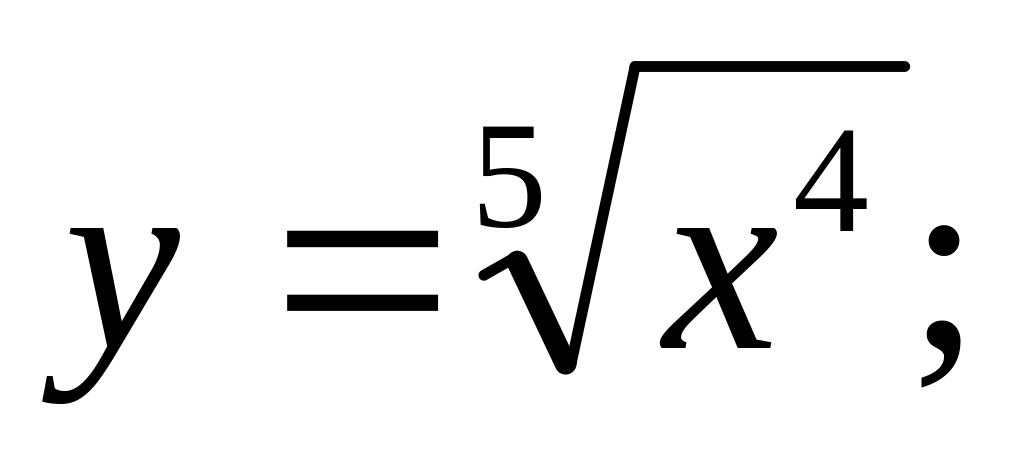 3)
3)
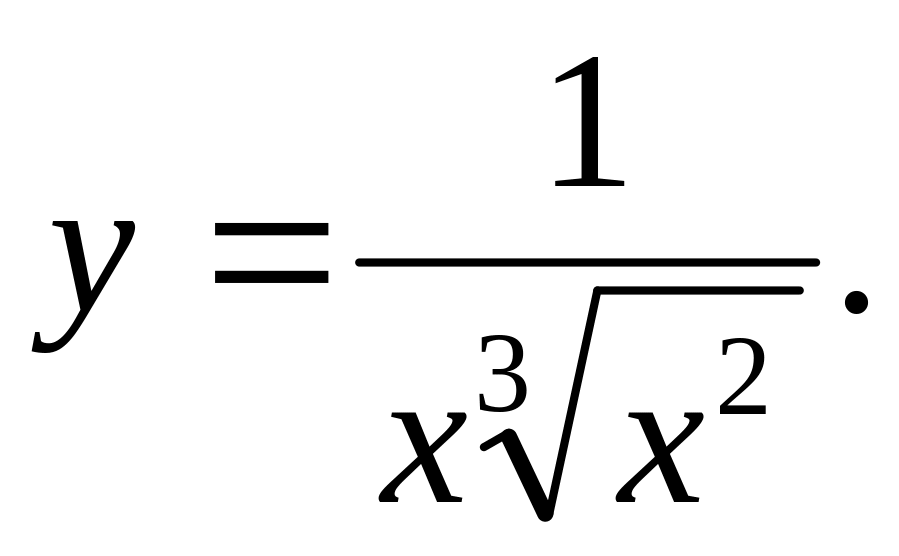
Решение.
Задача 3.
Найти производные, если
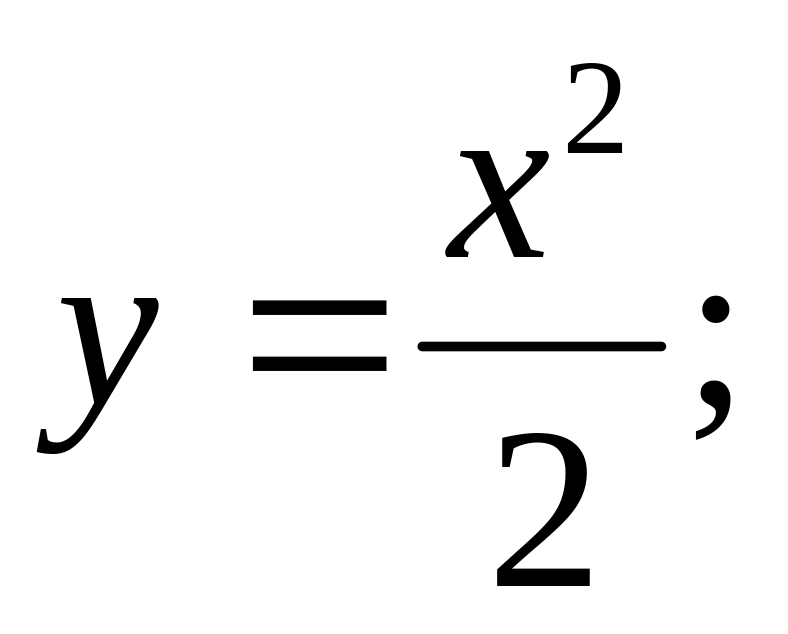 2)
2)

Решение.
1)
![]()
Задача 4.
Найти , если
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
Решение.
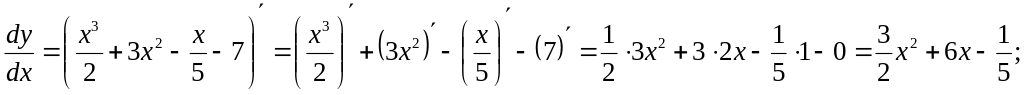
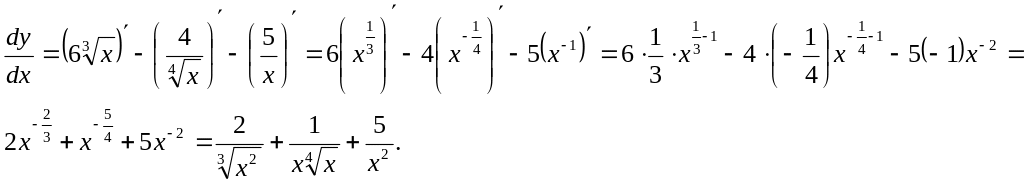 3)
3)
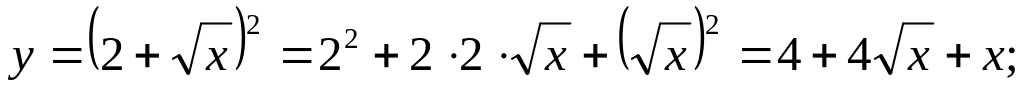
![]()
4)Предварительно разделим почленно числитель на знаменатель
![]()
![]()
Задача 5.
Найти производные следующих функций
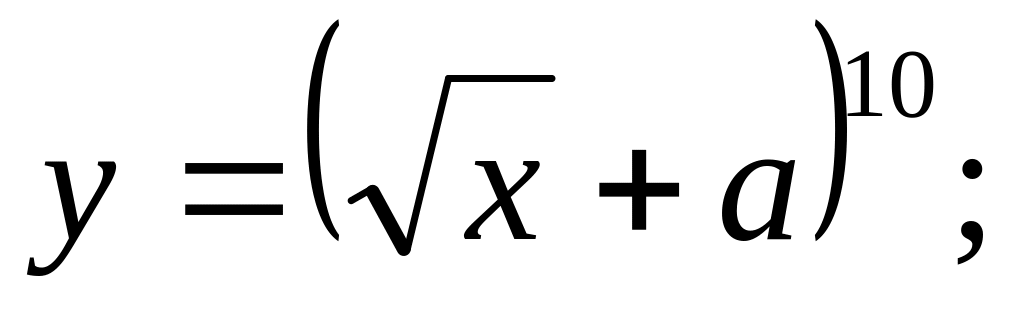 Ответ:
Ответ:
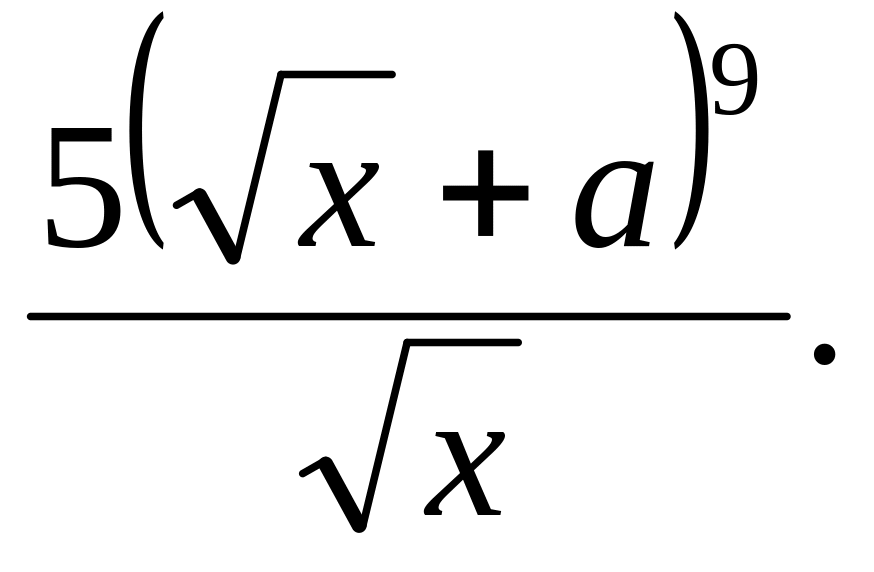
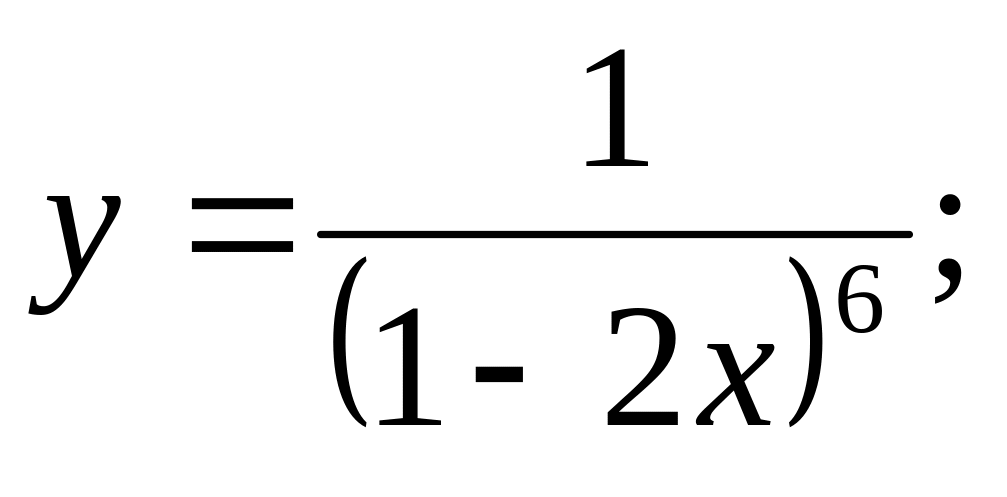 Ответ:
Ответ:
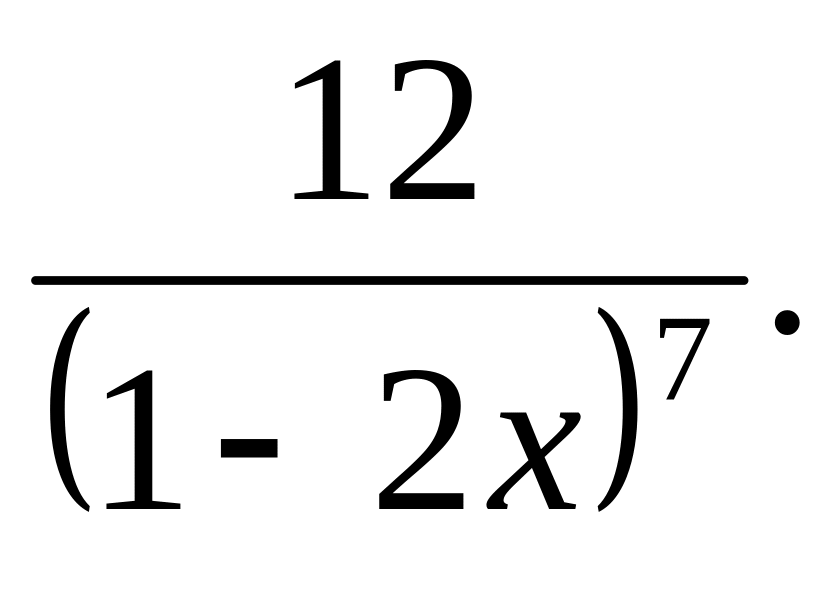
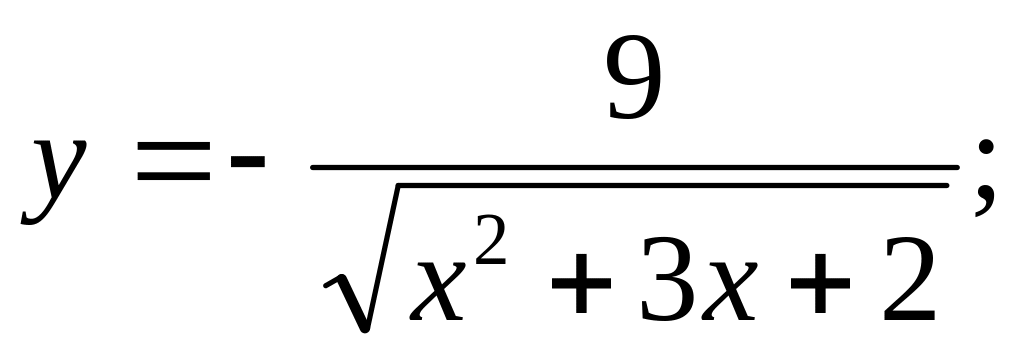 Ответ:
Ответ:
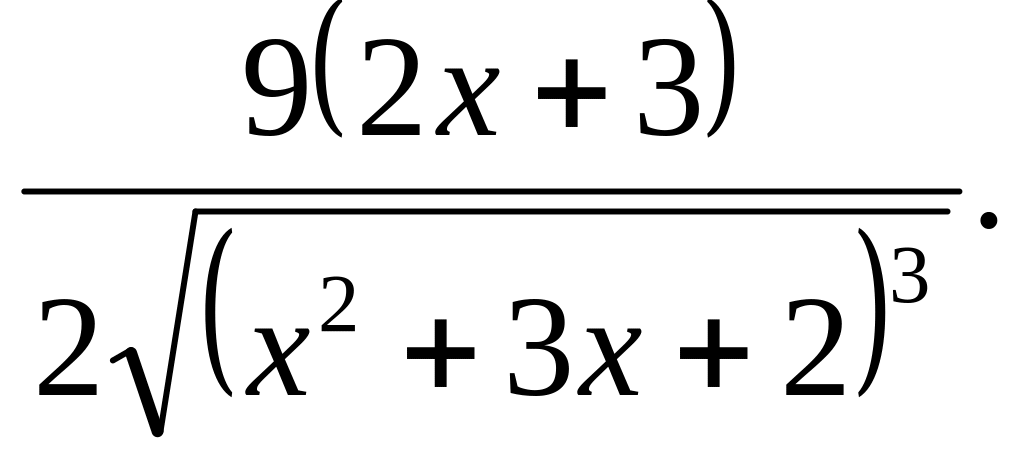
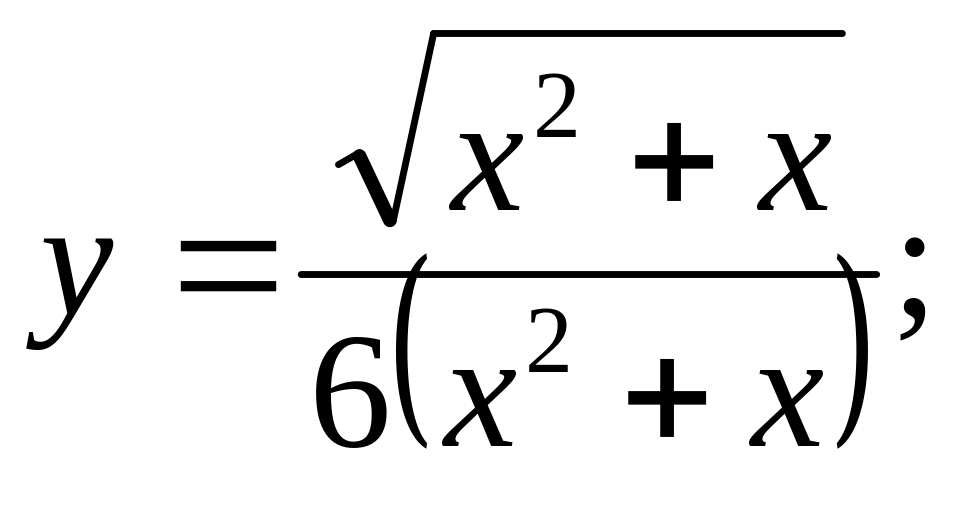 Ответ:
Ответ:
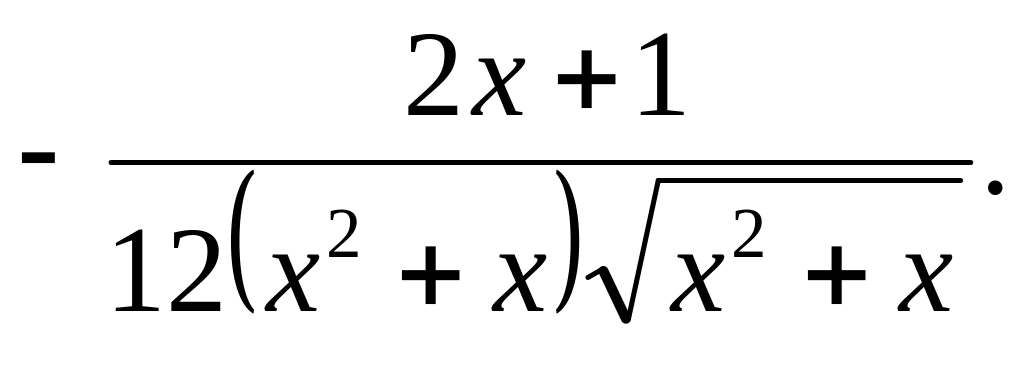
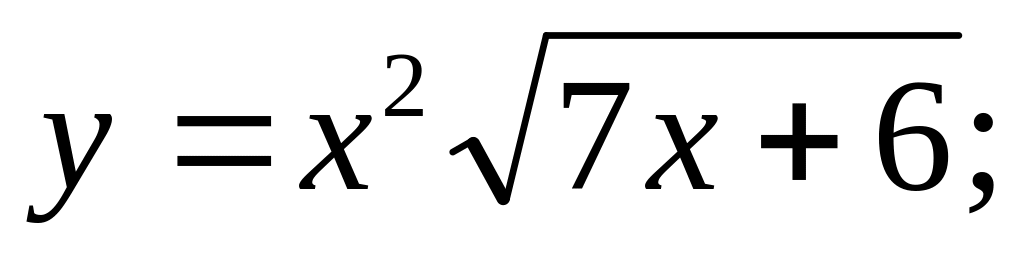 Ответ:
Ответ:
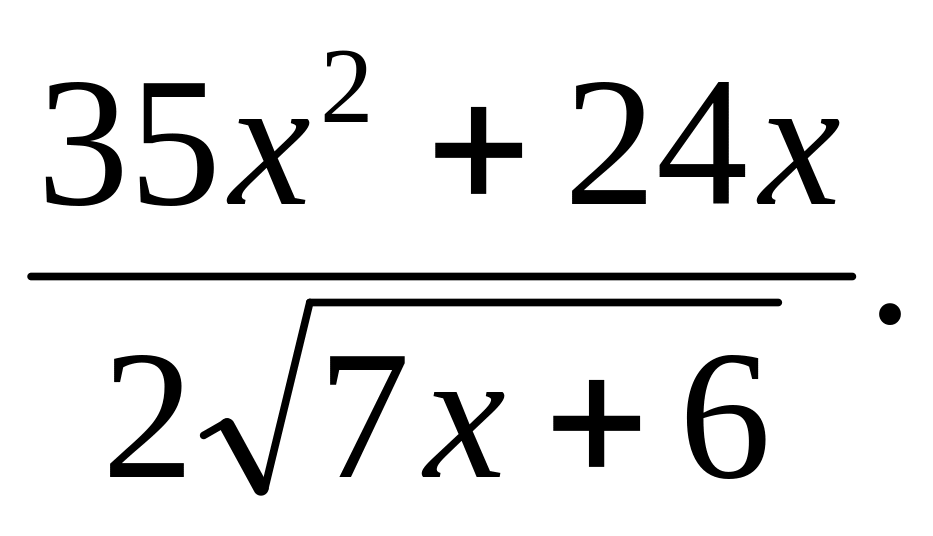
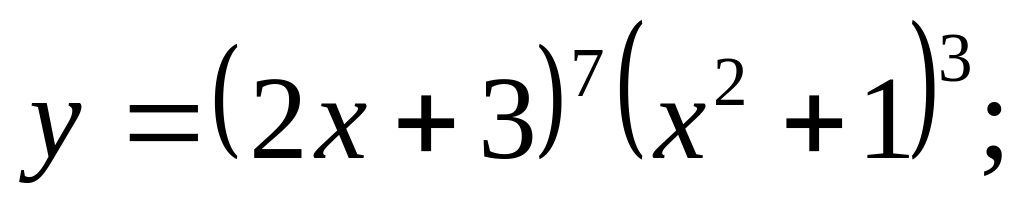 Ответ:
Ответ:
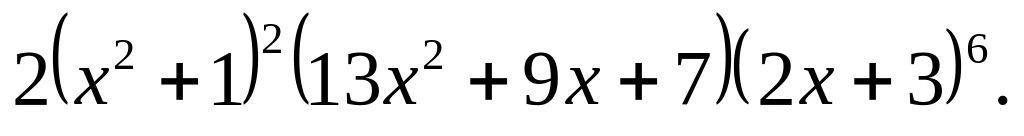
Задача 6.
Найти производные
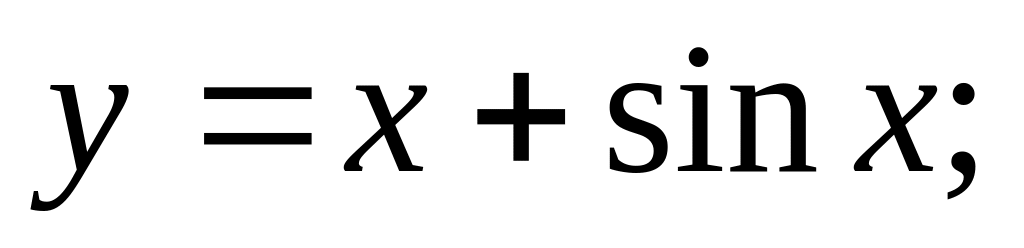 Ответ:
Ответ: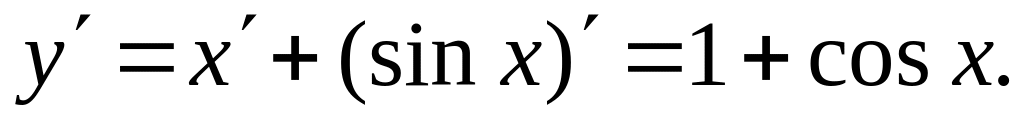
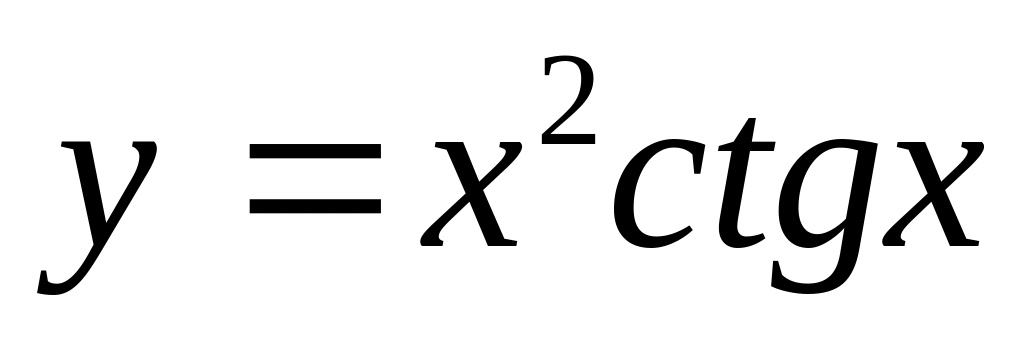 ;
Ответ:
;
Ответ: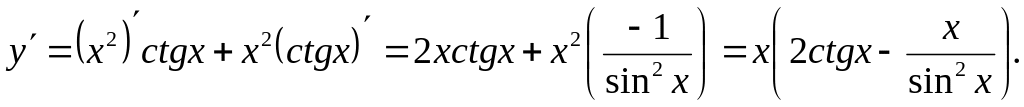
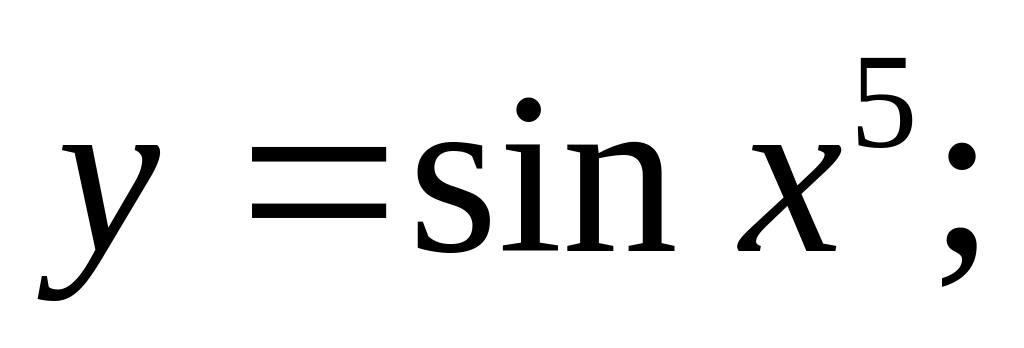 Ответ:
Ответ: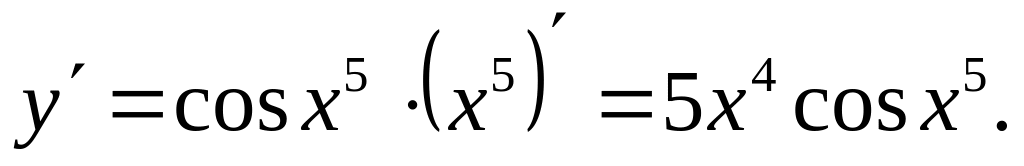
 Ответ:
Ответ: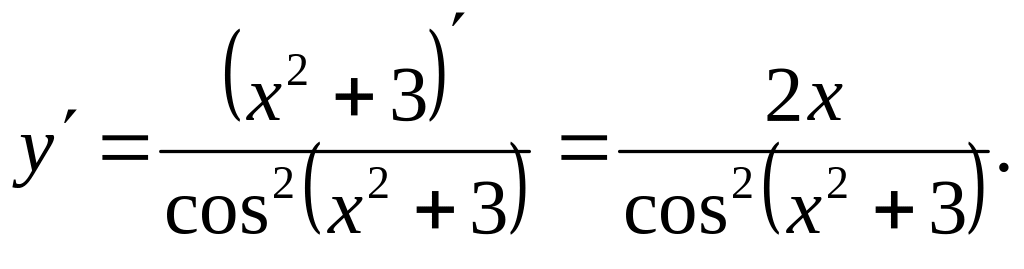
 Ответ:
Ответ: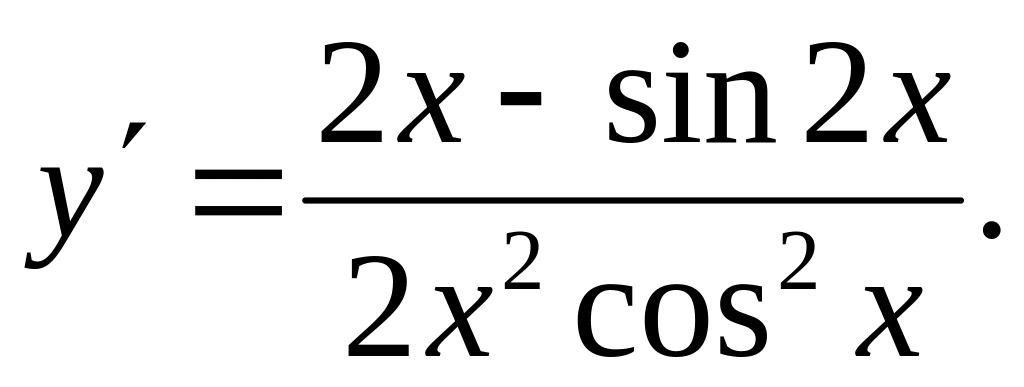
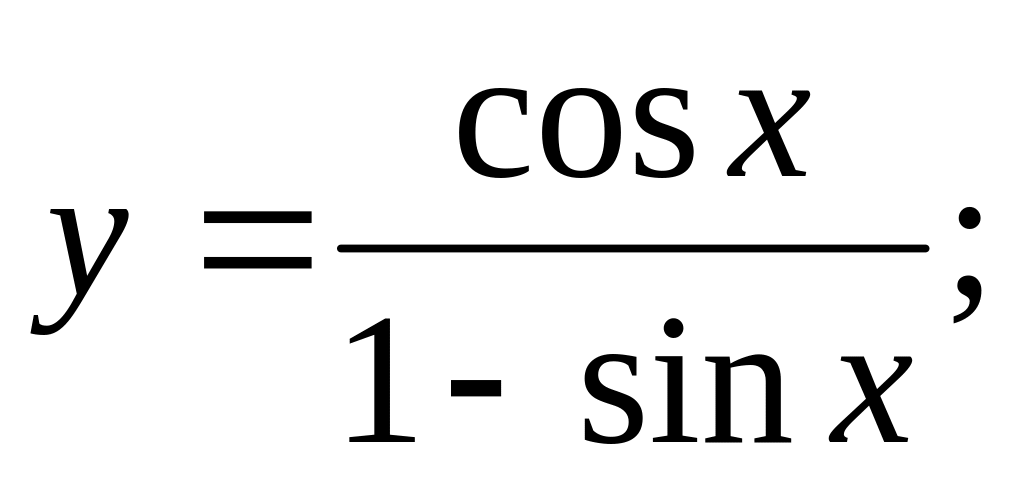 Ответ:
Ответ: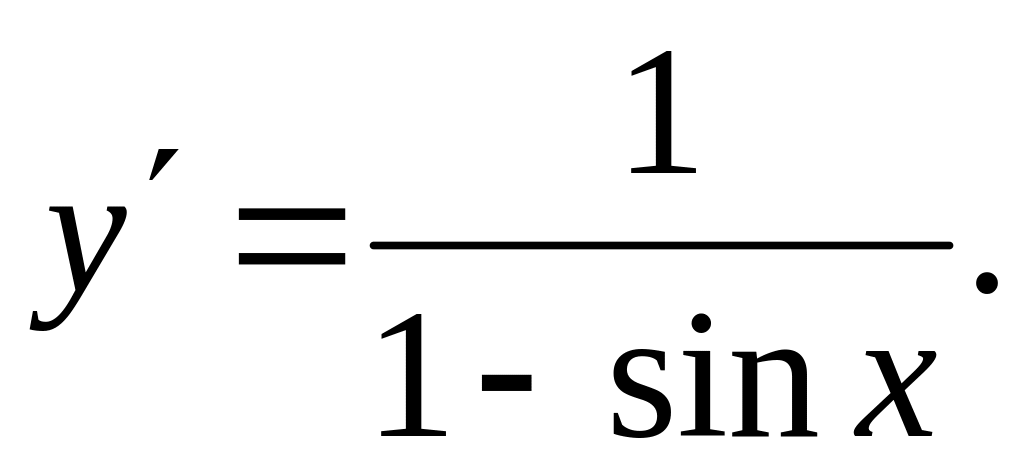
Задача 7.
Найти производную
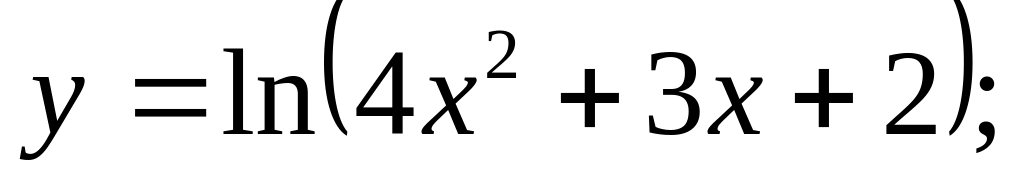 Ответ:
Ответ: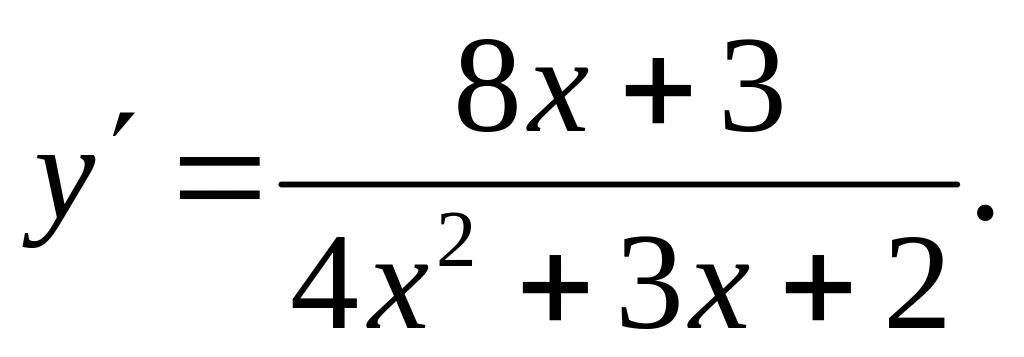
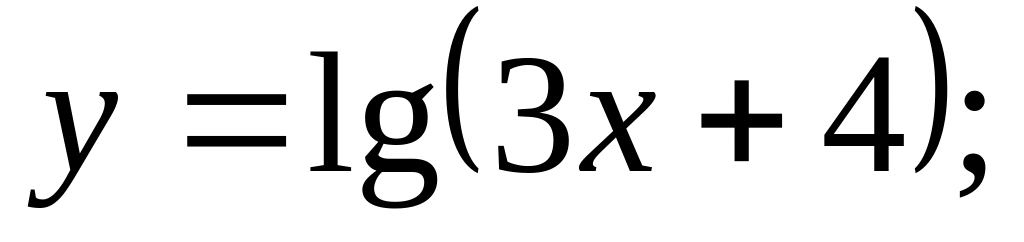 Ответ:
Ответ: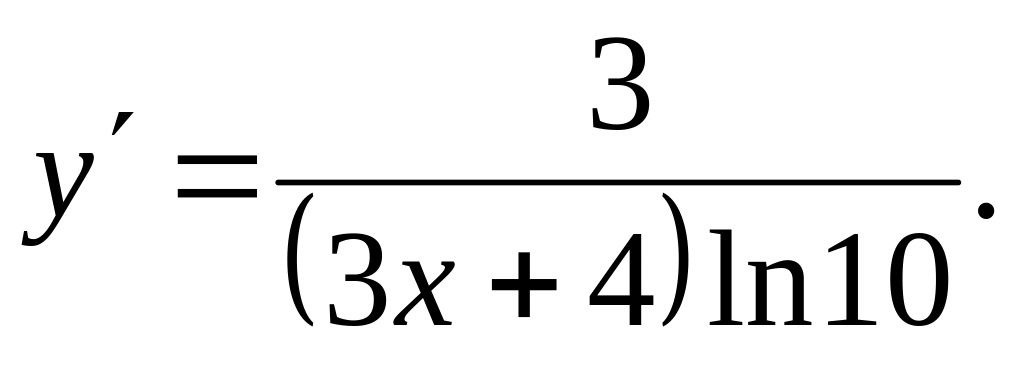
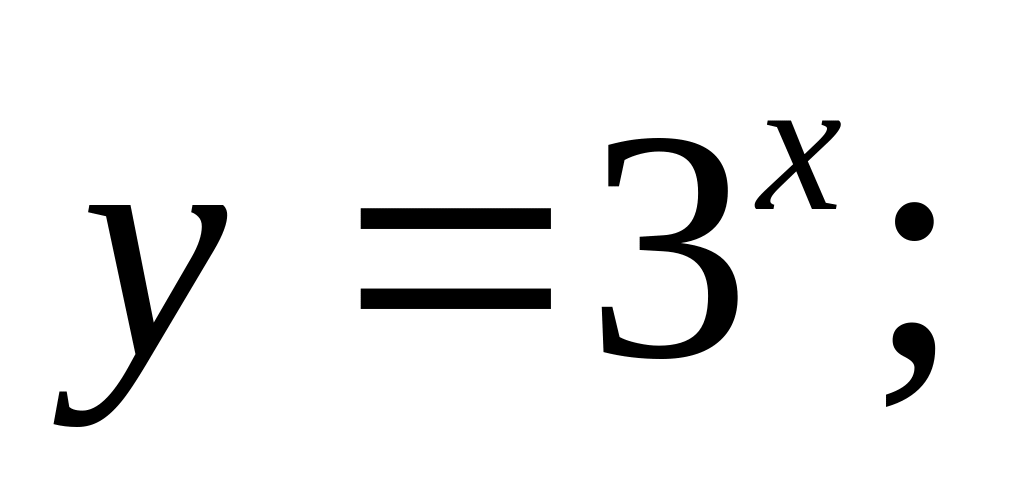 Ответ:
Ответ: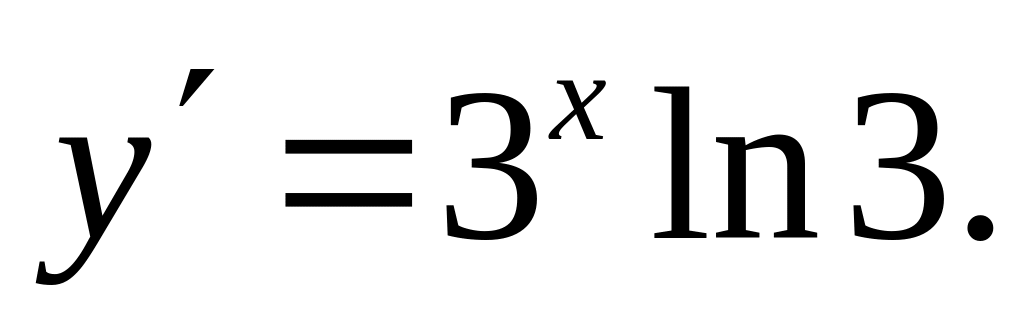
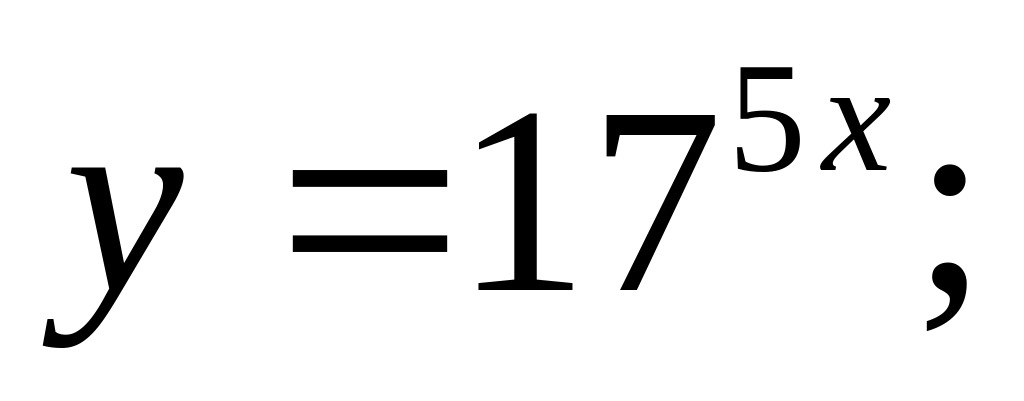 Ответ:
Ответ: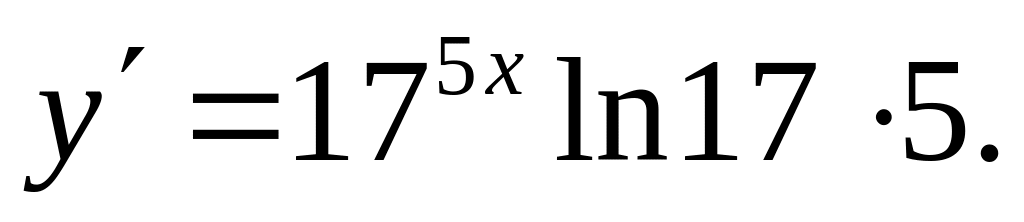
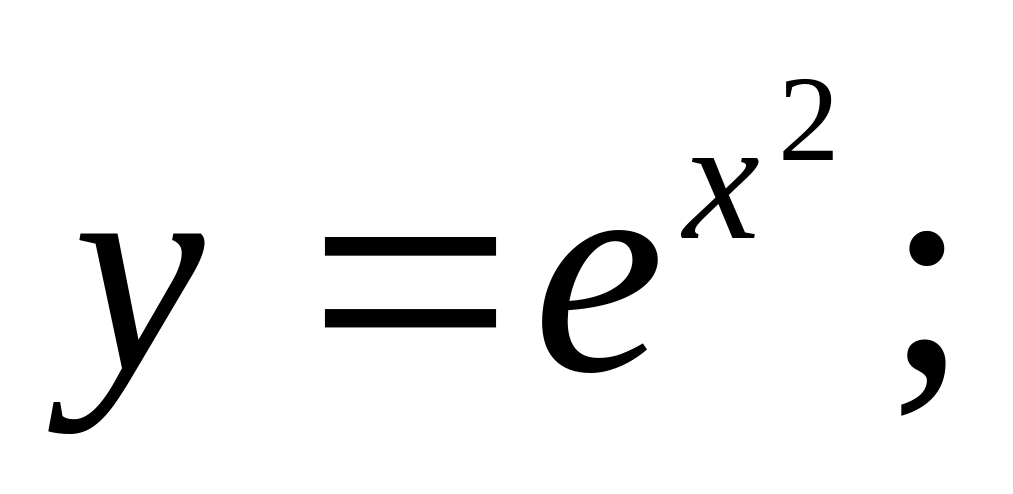 Ответ:
Ответ: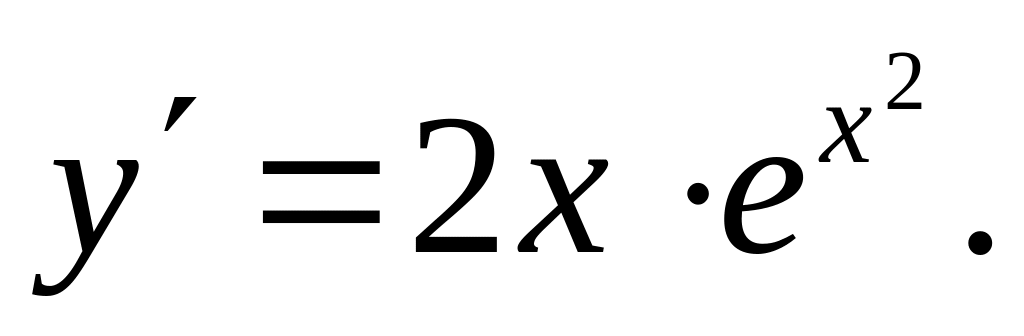
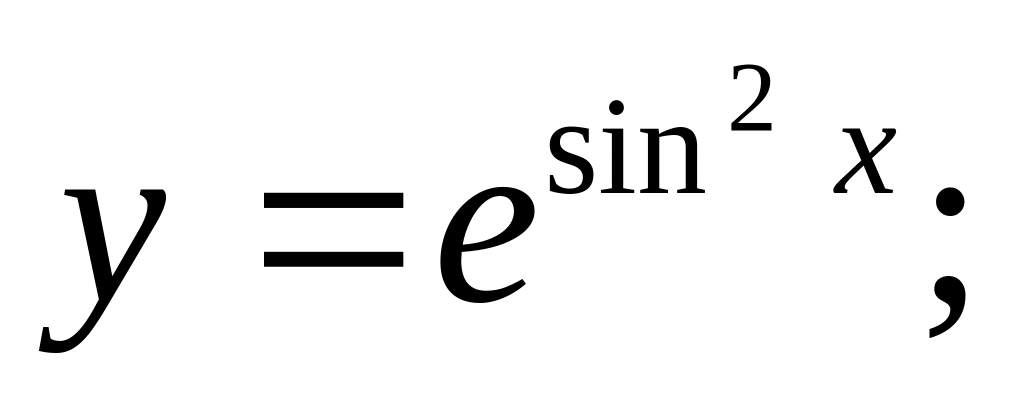 Ответ:
Ответ: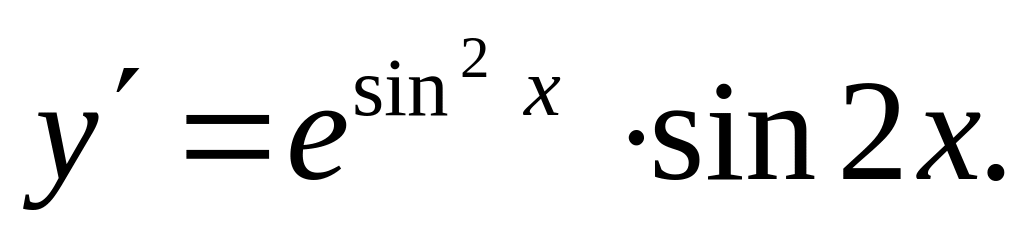
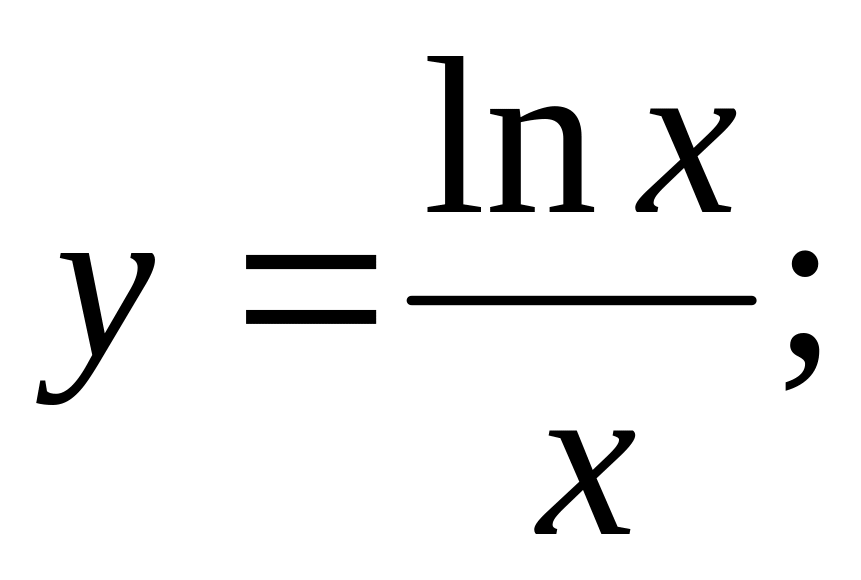 Ответ:
Ответ: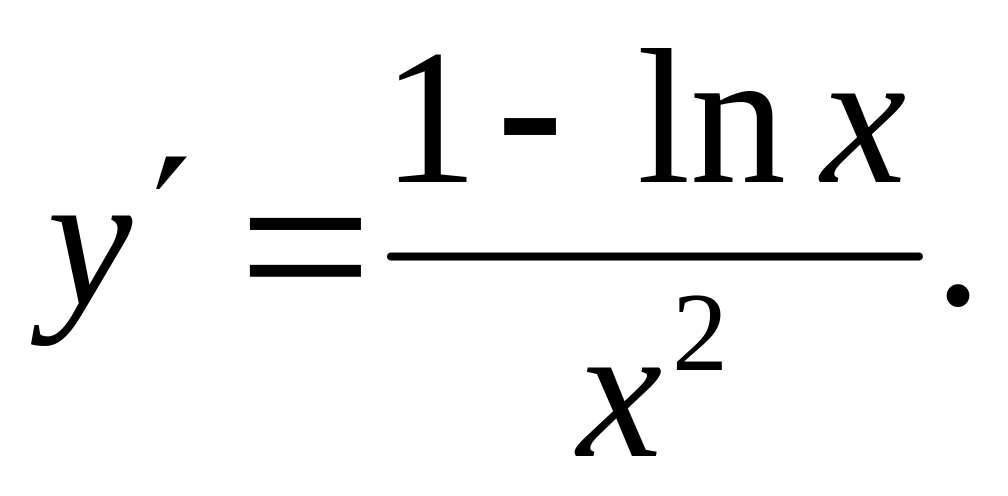
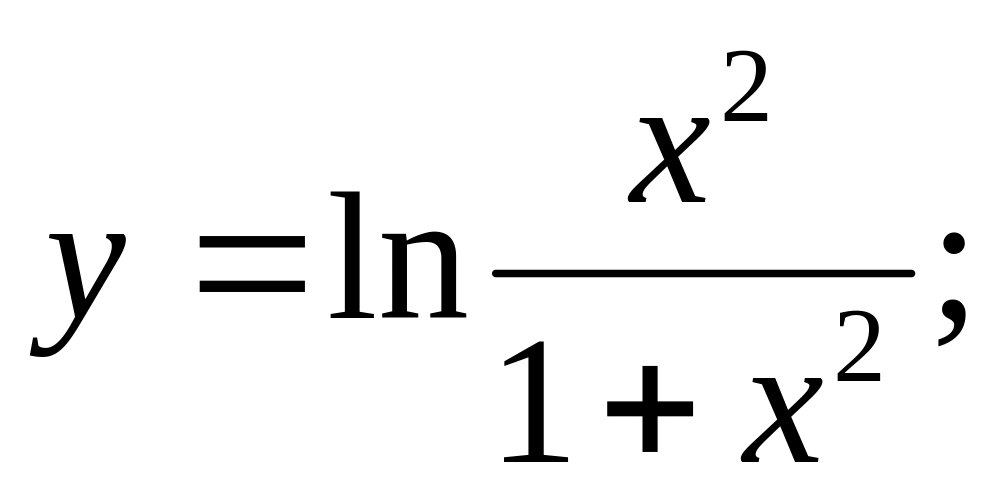 Ответ:
Ответ: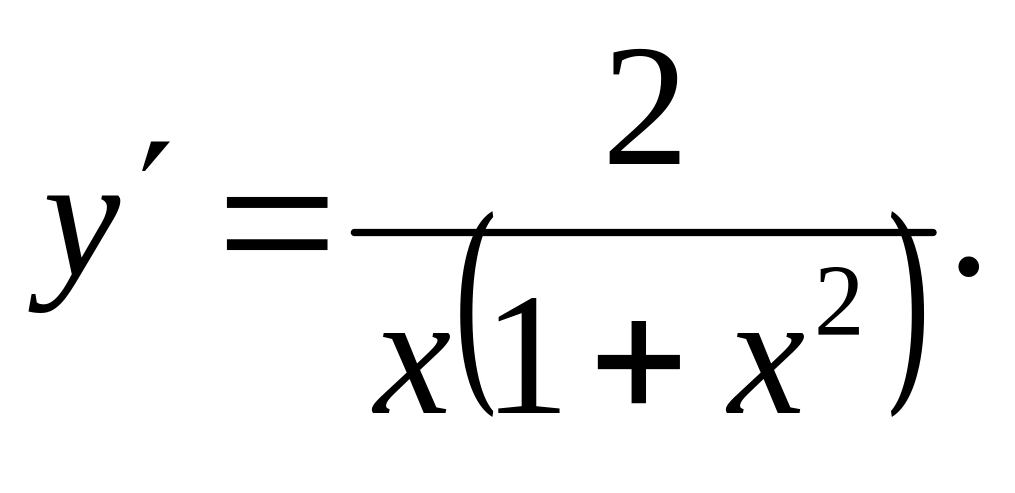
Задача 8.
Найти производные
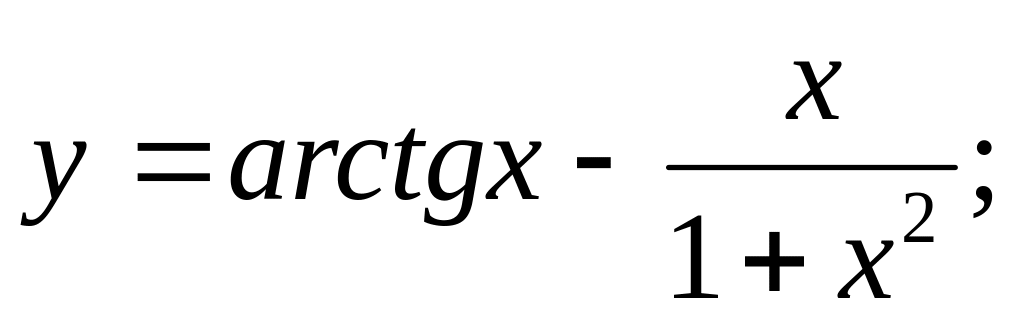 Ответ:
Ответ: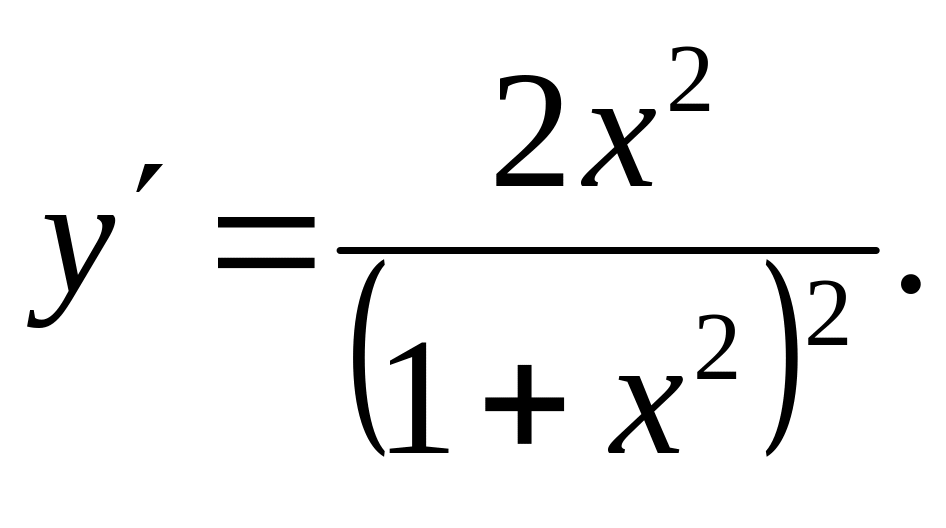
 Ответ:
Ответ:
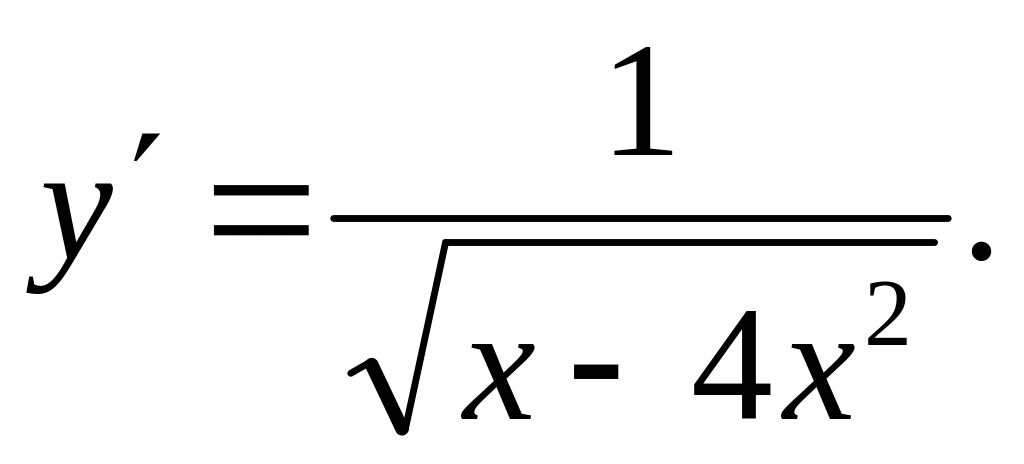
Задача 9.
Найти производные
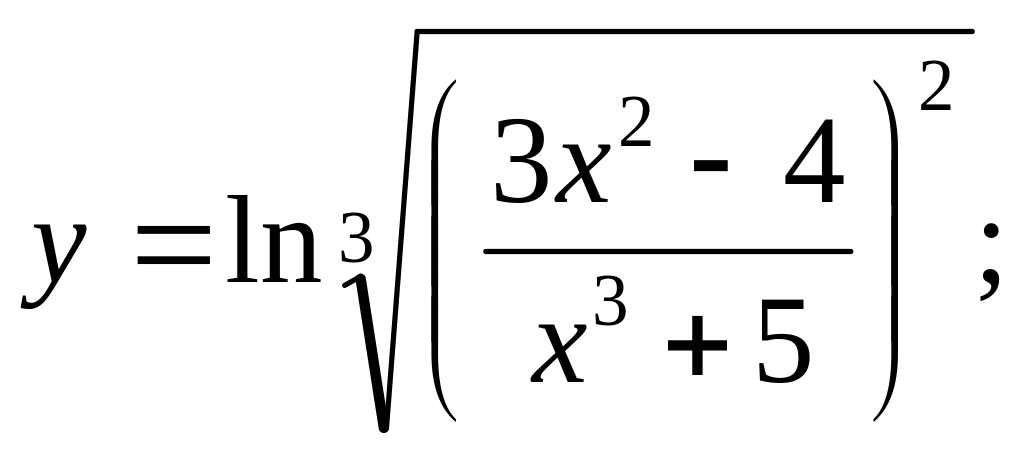 Ответ:
Ответ: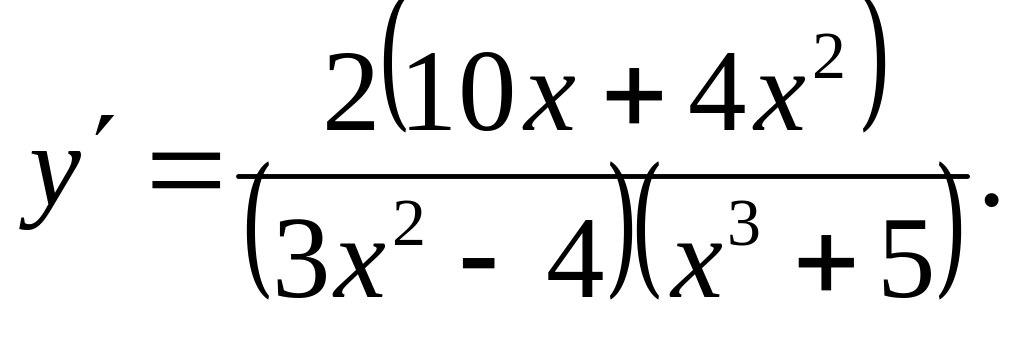
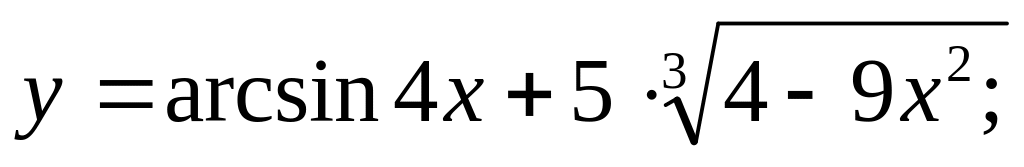 Ответ:
Ответ: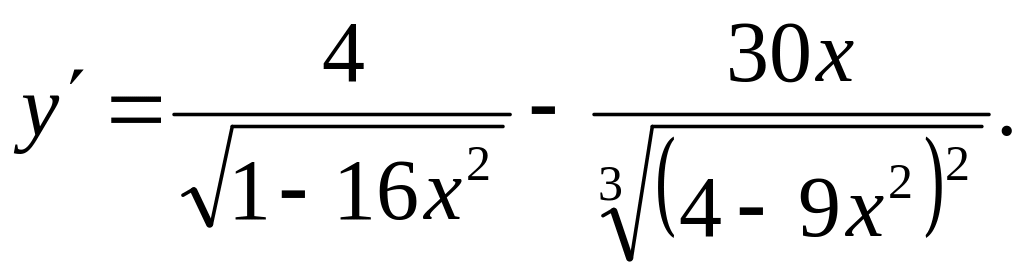
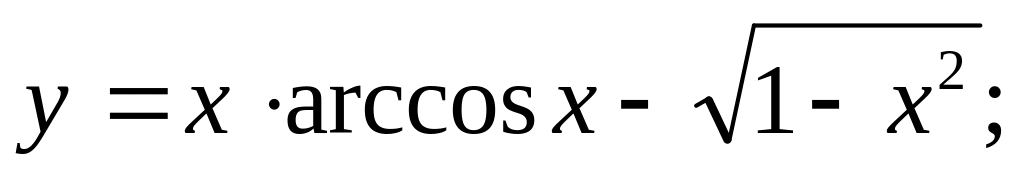 Ответ:
Ответ:
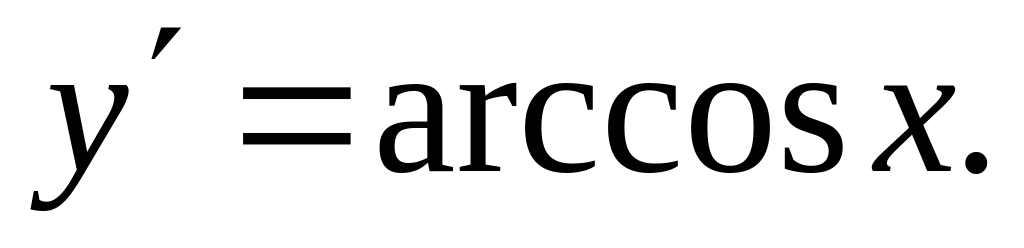
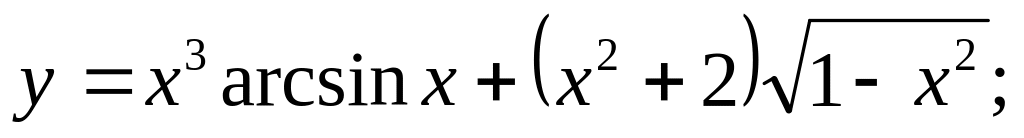 Ответ:
Ответ: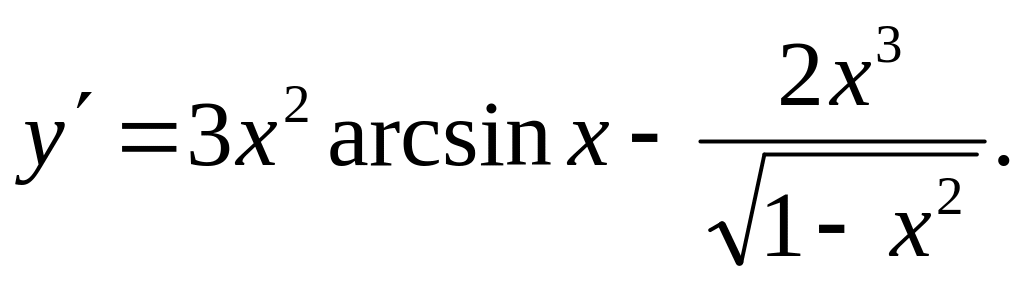
 Ответ:
Ответ: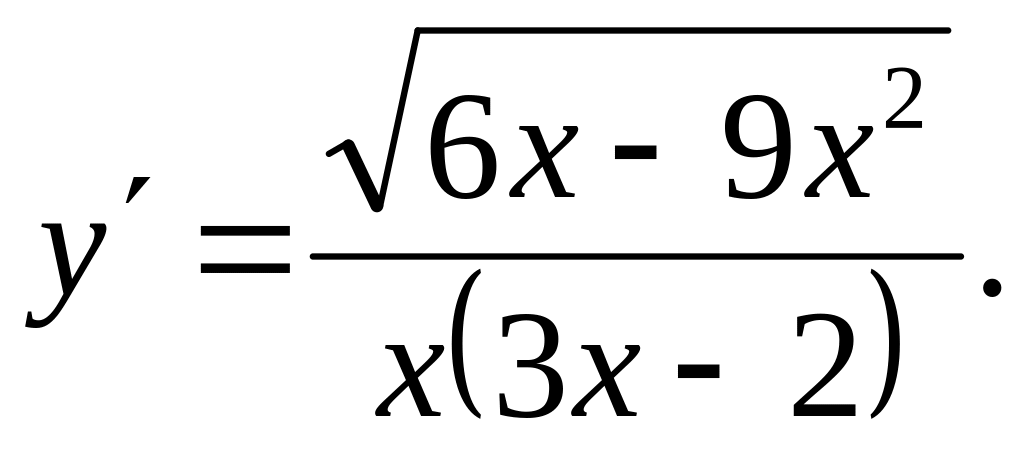
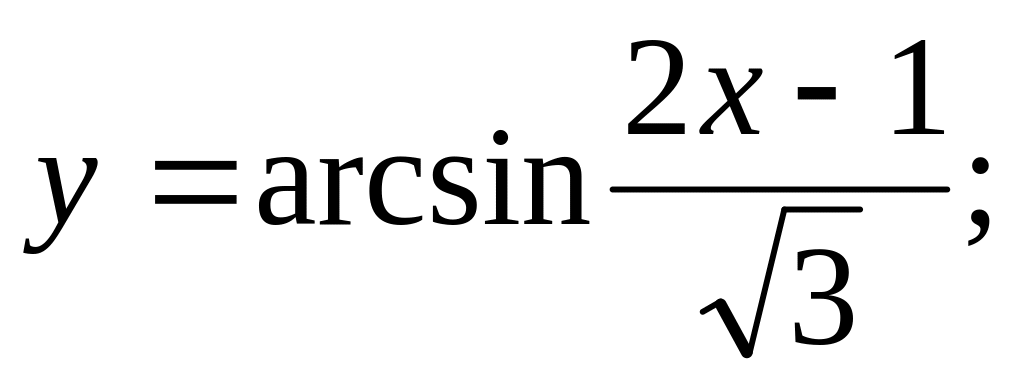 Ответ:
Ответ:
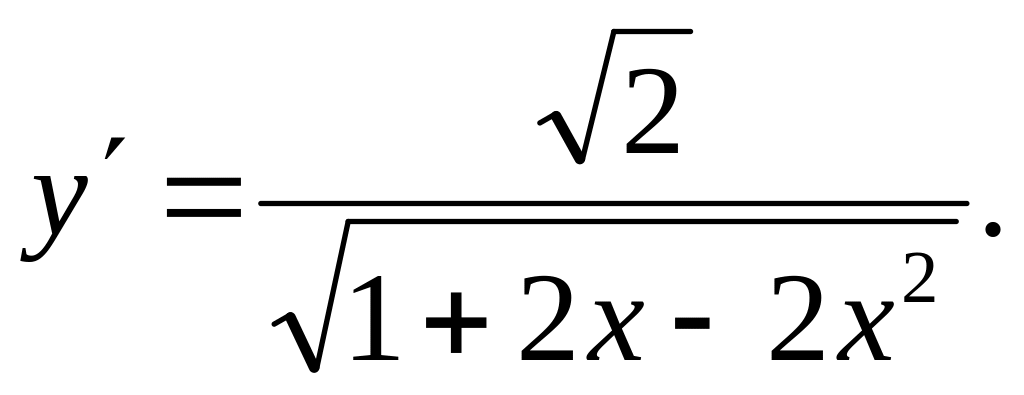
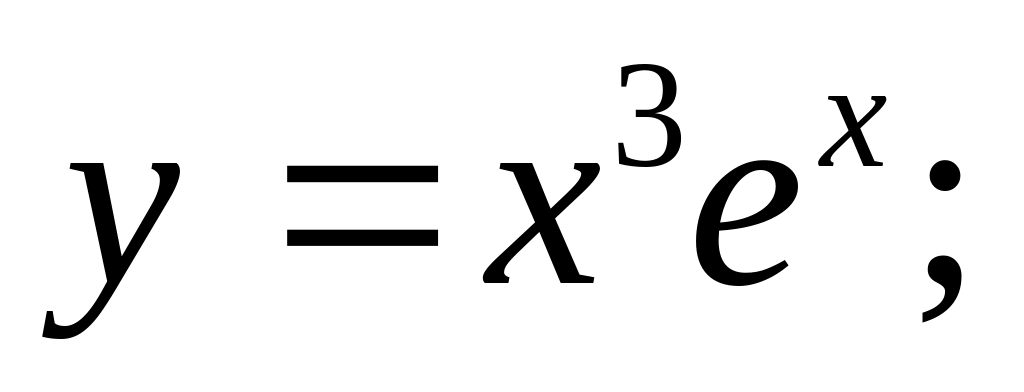 Ответ:
Ответ:
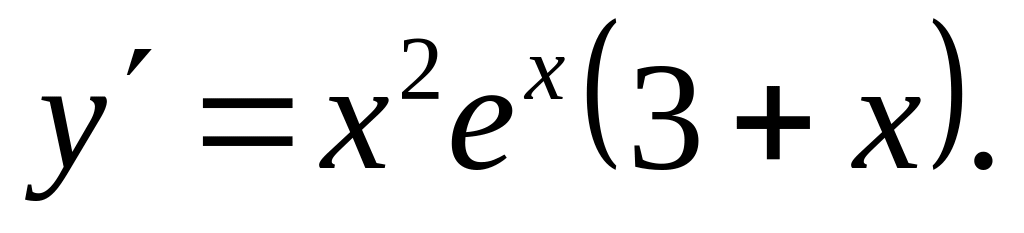
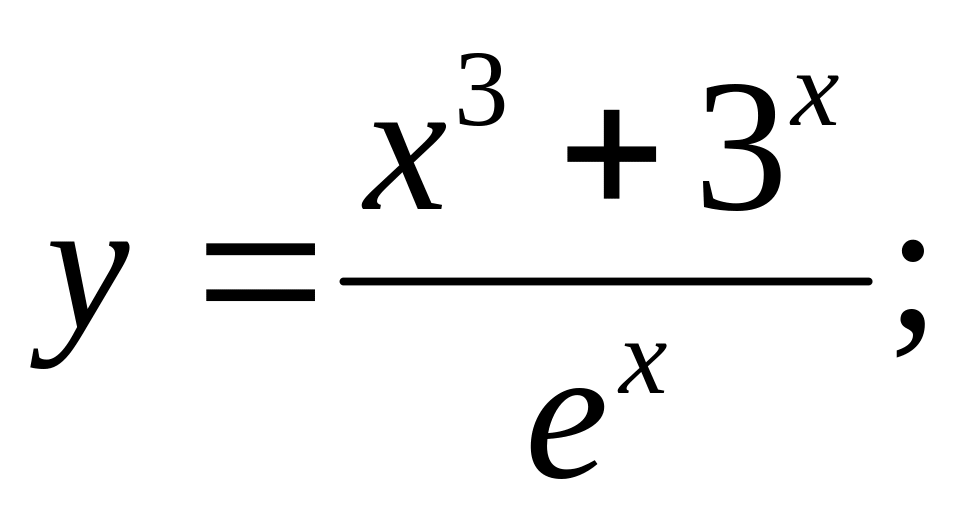 Ответ:
Ответ:
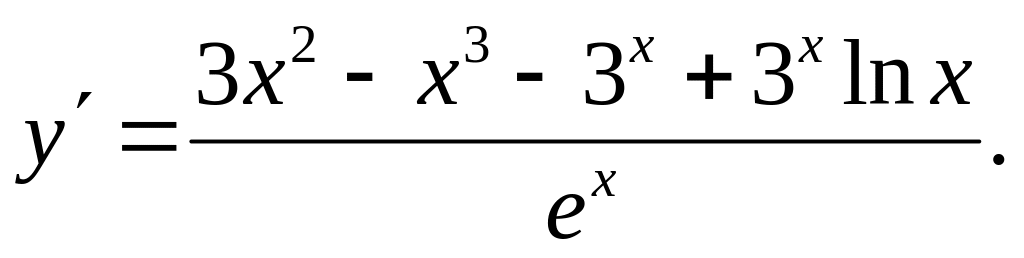
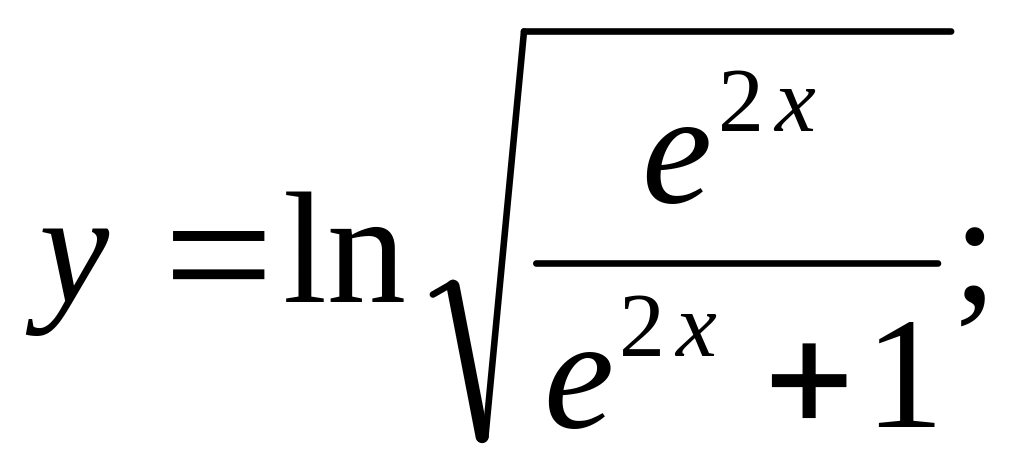 Ответ:
Ответ:
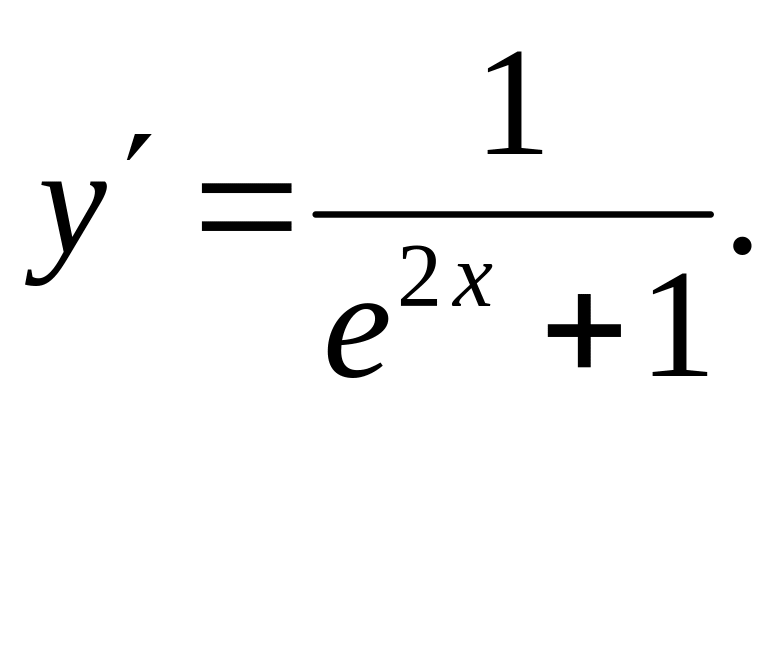
 Ответ:
Ответ:
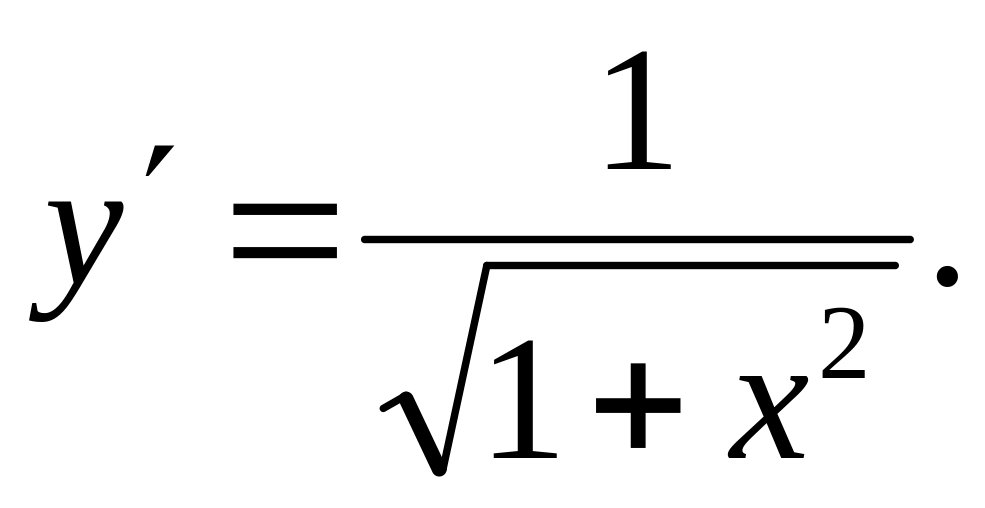
Задача 10.
Найти
дифференциал функции
![]() .
.
Решение.
Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал функции
![]()
Задача 11.
Дана
функция вида
![]() Вычислить ее дифференциал при х=0; dx=0,1.
Вычислить ее дифференциал при х=0; dx=0,1.
Решение.
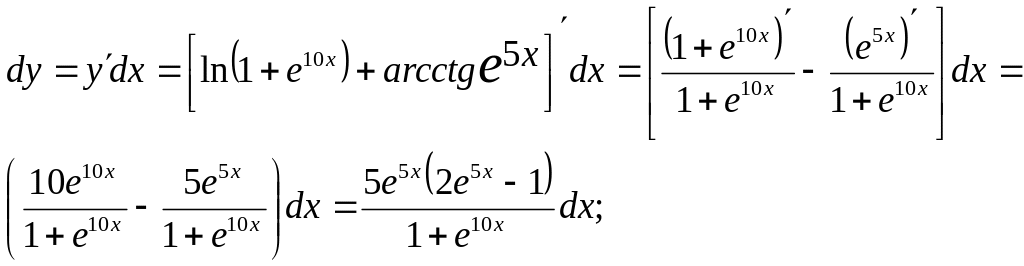
полагая х=0; dx=0,1
![]()
Задача 12.
Вычислить
значение дифференциала функции
![]() при х=4; dx=0,01.
при х=4; dx=0,01.
Решение.
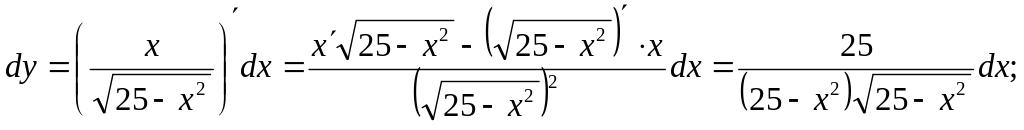
![]()
Задача 13.
При
помощи дифференциала найти приближенное
значение функции
![]() при х=1,02.
при х=1,02.
Решение.
Применим формулу
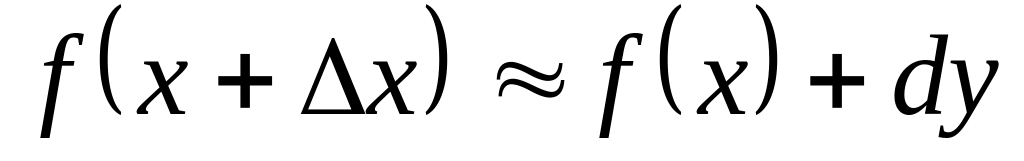 ,
считая что х=1 и dx=0,02.
Получим
,
считая что х=1 и dx=0,02.
Получим
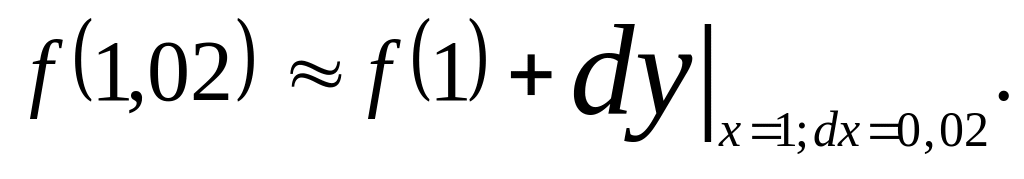
Вычислим слагаемые
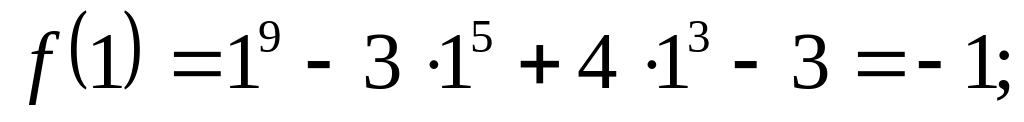

![]()
Задача 14.
При
помощи дифференциала найти приближенное
значение
![]()
Решение.
Будем
рассматривать
как частное значение функции
![]() при х=17. Выберем ближайшее удобное
значение
при х=17. Выберем ближайшее удобное
значение
![]() .
.
Тогда

Найдем производную

Вычислим
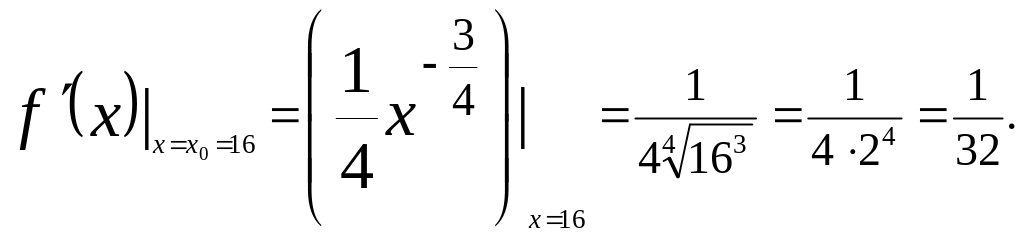
Вычислим
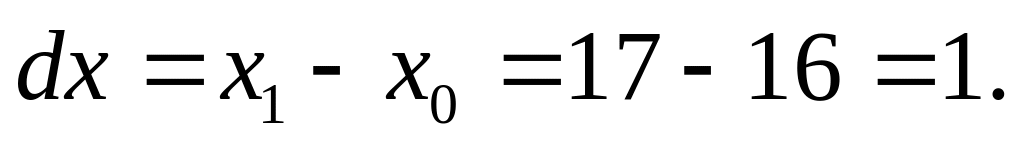
Найдем приближенное значение функции
![]()
Задача 15.
При
помощи дифференциала найти приближенное
значение
![]()
Решение.
Будем рассматривать как частное значение функции
 при х=35.
при х=35.Выберем удобное значение
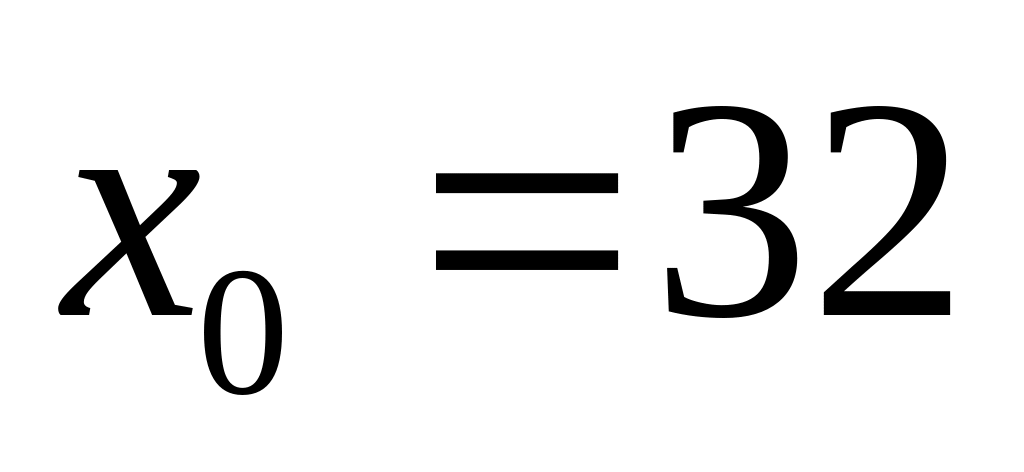 ,
тогда
,
тогда
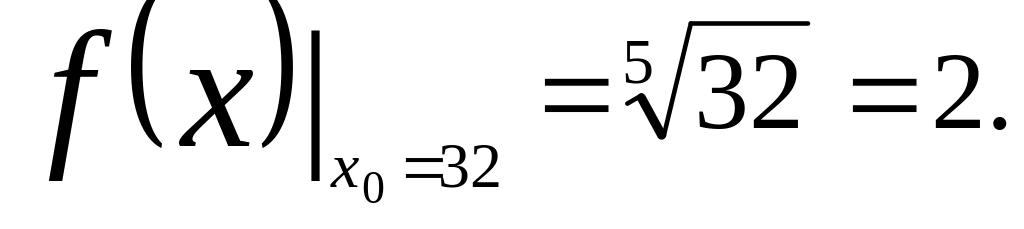
Вычислим
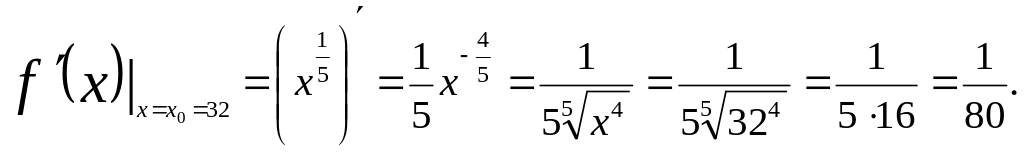
Вычислим
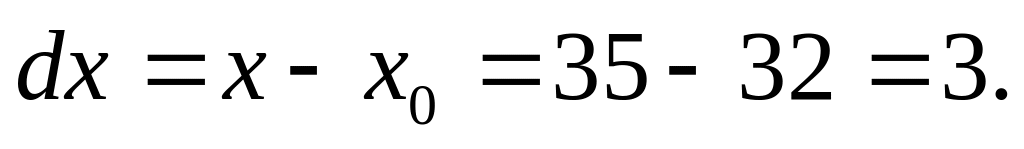
Найдем приближенное значение
![]()
Задача 16.
Вычислить
приближенно
![]()
Решение.
Полагая,
что
![]() есть частное значение функции
при
есть частное значение функции
при
![]() .
Ближайшее значение
.
Ближайшее значение
![]() выразим в радианах
выразим в радианах
![]() .
Вычислим
.
Вычислим
![]()
![]()
![]()
![]()
Задача 17.
Вычислить
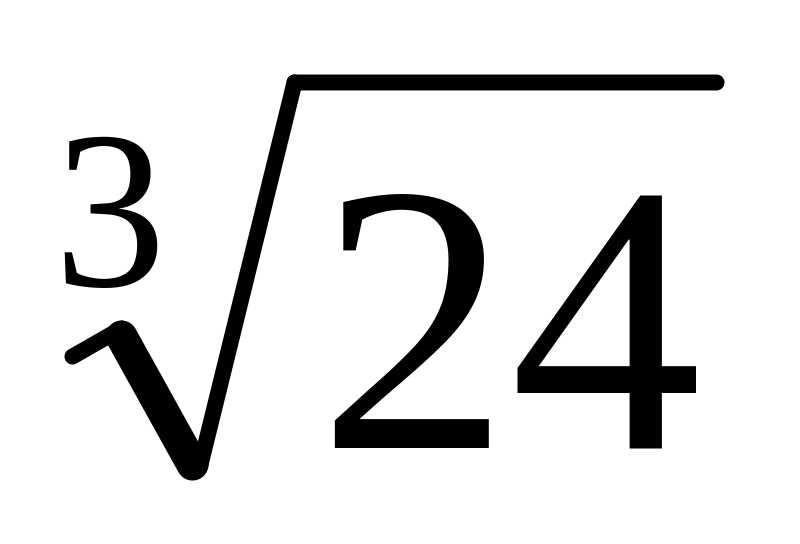 ;
Ответ: 2,89.
;
Ответ: 2,89.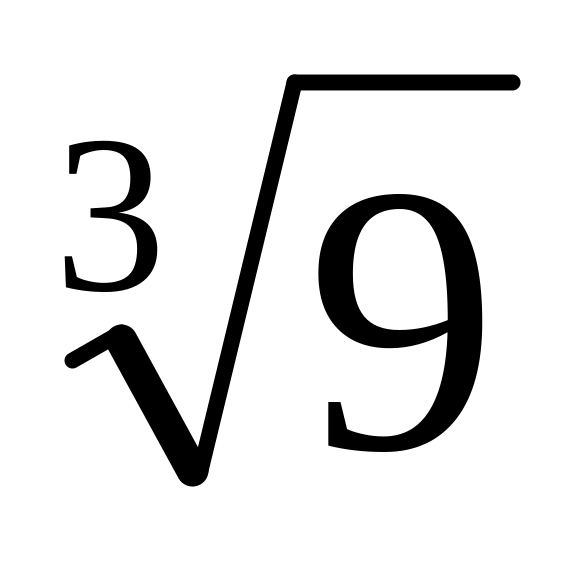 ;
Ответ: 2,08.
;
Ответ: 2,08.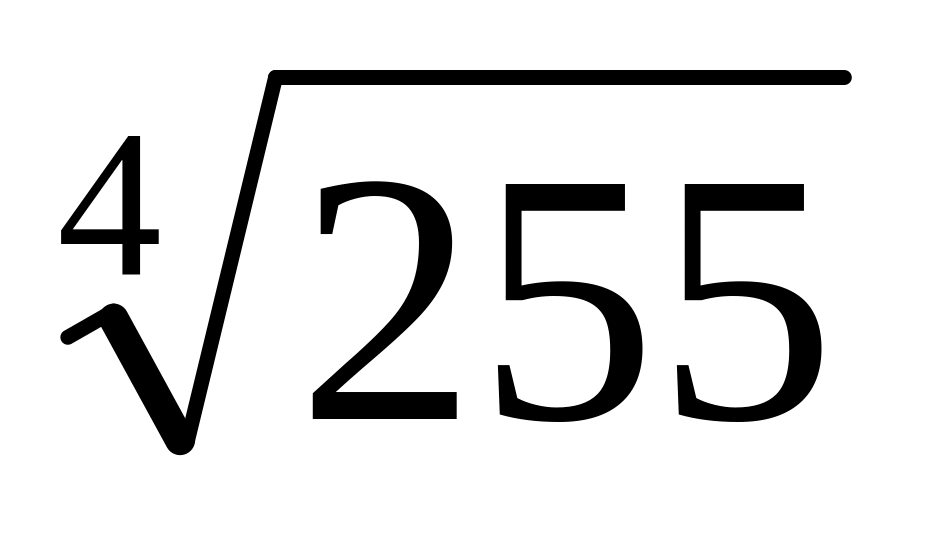 ;
Ответ: 3,9961.
;
Ответ: 3,9961.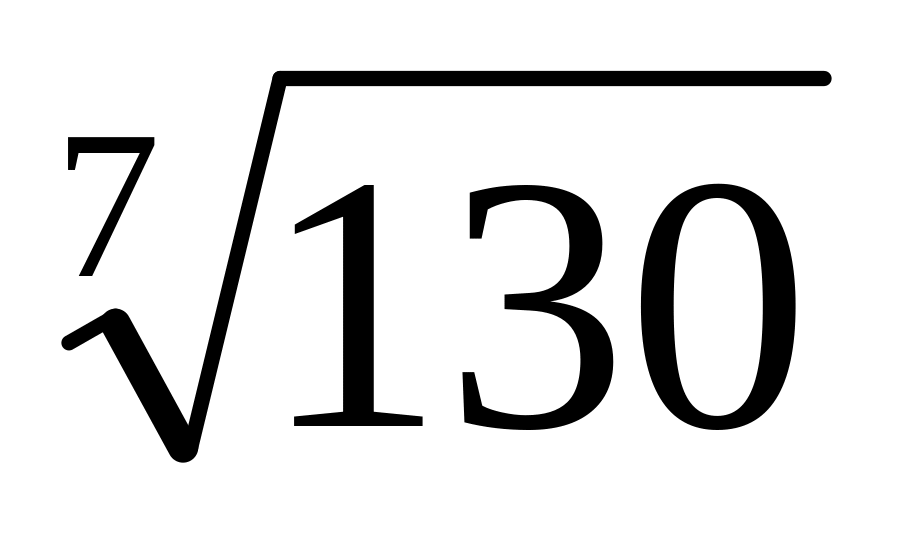 ;
Ответ: 2,0045.
;
Ответ: 2,0045.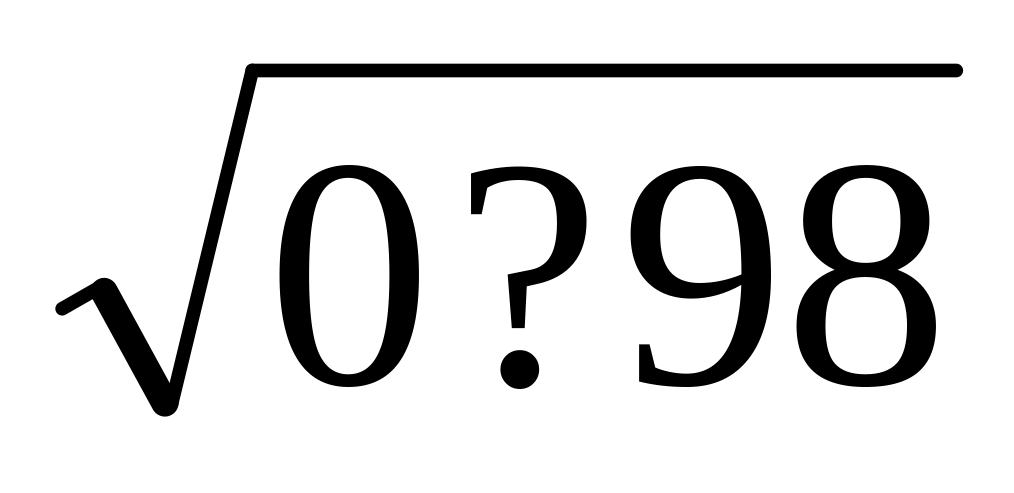 ;
Ответ: 0,99.
;
Ответ: 0,99.
Глава 5. Элементы интегрального исчисления.
5.1. Определение интегрирования.
Интегрированием называется действие, обратное дифференцированию, то есть восстановление функции по данной производной или по данному дифференциалу.
Пусть
![]() - производная от функции
- производная от функции
![]() во всех точках некоторого интервала
или, что то же самое,
во всех точках некоторого интервала
или, что то же самое,
![]() есть дифференциал функции
в том же интервале. Тогда функция
называется первообразной для функции
или дифференциала
.
Отыскание первообразной функции и есть
интегрирование.
есть дифференциал функции
в том же интервале. Тогда функция
называется первообразной для функции
или дифференциала
.
Отыскание первообразной функции и есть
интегрирование.
5.2. Неопределенный интеграл.
Определение
1. Функция
называется первообразной функцией
от функции
,
если выполняется равенство
![]() (или, что то же самое,
(или, что то же самое,
![]() ).
).
Определение
2. Совокупность
![]() всех первообразных функций от функции
называется неопределенным интегралом
от этой функции и обозначается
всех первообразных функций от функции
называется неопределенным интегралом
от этой функции и обозначается
![]() ,
т.е.
,
т.е.
![]()
где
![]() -
знак интеграла,
-
знак интеграла,
- подынтегральная функция,
- подынтегральное выражение,
С – произвольная постоянная.
Свойства неопределенного интеграла:
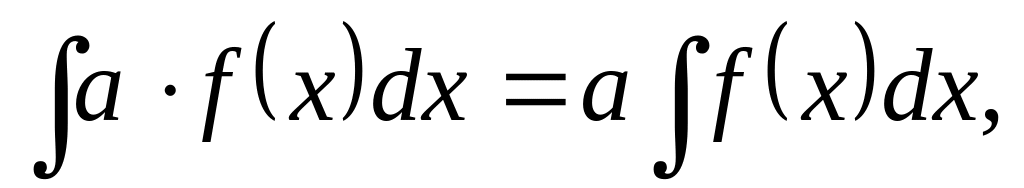 где
a – произвольная
постоянная;
где
a – произвольная
постоянная;