
- •Математика
- •Глава 1 элементы теории множеств
- •1.1 Понятие множества.
- •1.2. Элемент и принадлежность элемента к множеству. Операции над множествами
- •1.3. Действительные числа
- •Отрезок, интервал, окрестность
- •Глава 2 начала аналитической геометрии
- •2.1. Метод координат
- •Прямоугольная система координат на плоскости
- •2.2. Уравнение линии на плоскости
- •2.3. Расстояние между двумя точками на плоскости
- •2.4. Деление направленного отрезка в заданном отношении
- •2.5. Линии первого порядка
- •2.6. Расстояние от точки до прямой
- •2.7. Взаимное расположение двух прямых на плоскости
- •2.8. Линии второго порядка
- •2.9. Решение задач
- •Глава 3. Введение в анализ. Пределы
- •3.1. Понятие функции. График функции
- •3.2. Элементарные функции и их графики
- •3.3. Предел числовой последовательности
- •3.4. Предел функции
- •3.5. Бесконечно малые и бесконечно большие величины
- •3.6. Основные теоремы о пределах
- •3.7 Вычисление пределов
- •3.8. Непрерывность функции. Точки разрыва
- •3.9. Решение задач
- •Глава 4. Дифференциальное исчисление.
- •4.1. Понятие производной.
- •4.2. Геометрический смысл производной.
- •4.4. Основные формулы дифференцирования.
- •4.5. Дифференциал функции.
- •Приближенные вычисления с помощью дифференциала.
- •4.6. Решение задач
- •Продифференцировать следующие функции
- •Глава 5. Элементы интегрального исчисления.
- •5.1. Определение интегрирования.
- •5.2. Неопределенный интеграл.
- •5.3. Таблица простейших интегралов.
- •5.4. Непосредственное интегрирование
- •5.5. Методы интегрирования
- •Метод основан на использовании формулы дифференцирования произведения двух функций. Пусть u и V дифференцируемые функции от х. Тогда
- •Глава 6. Элементы теории вероятностей
- •6.1. Предмет теории вероятностей
- •6.2. Классическое определение вероятности
- •6.3. Теоремы сложения и умножения вероятностей
- •6.4. Формула полной вероятности
- •6.5. Формулы Байеса
- •6.6.Схема Бернулли
- •6.7. Закон распределения и числовые характеристики дискретной случайной величины
- •6.8. Решение задач
4.2. Геометрический смысл производной.
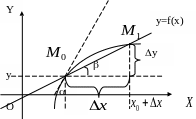
![]() -
секущая,
-
секущая,
![]() - приращение аргумента, у
– приращение функции.
- приращение аргумента, у
– приращение функции.
![]() -
угловой коэффициент секущей;
-
угловой коэффициент секущей;
![]() -
угловой коэффициент касательной.
-
угловой коэффициент касательной.
Т.е.
![]() .
.
Геометрический
смысл производной: производная функция
в точке
равна угловому коэффициенту касательной,
проведенной к графику этой функции в
точке
![]() с абсциссой
.
с абсциссой
.
4.3. Основные правила и формулы дифференцирования.
Нахождение производной по ее определению (через предел) требует громоздких вычислений. Поэтому на практике для нахождения производной выводят формулы производных основных элементарных функций. Затем, используя правила дифференцирования, выражают производную любой функции через эти уже известные производные.
Основные правила дифференцирования.
Пусть С=const, а u=u(x), v=v(x) – дифференцируемые на некотором множестве функции. Тогда
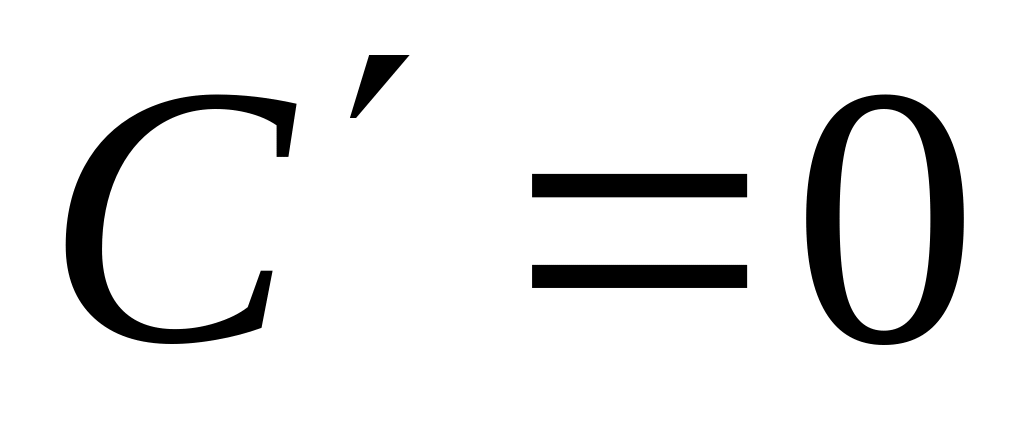 ;
;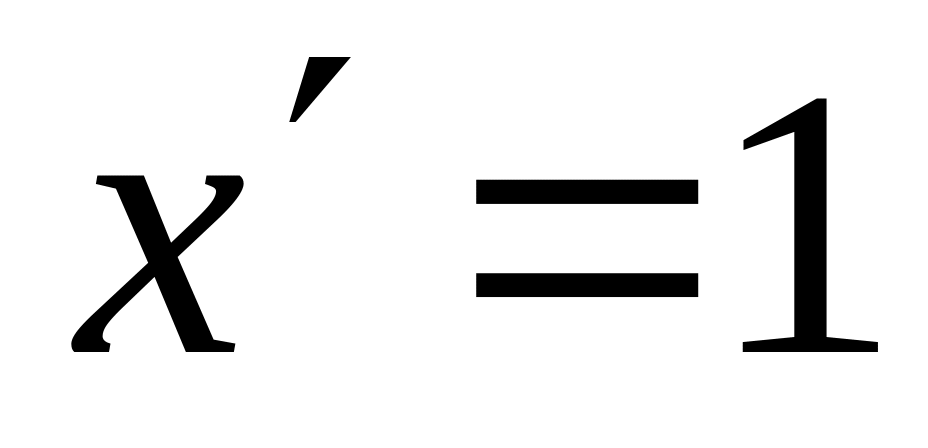 ;
;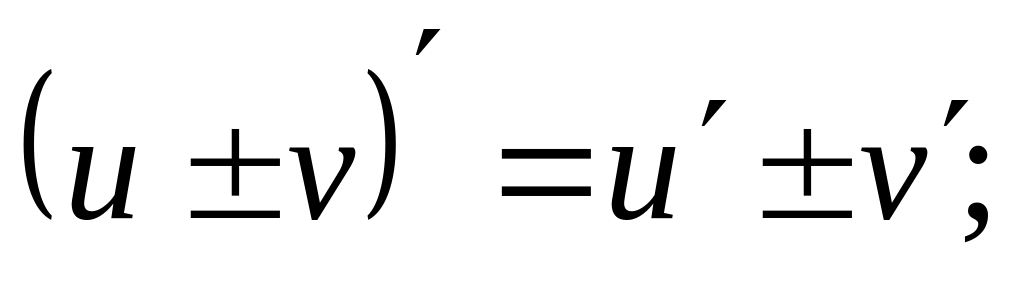
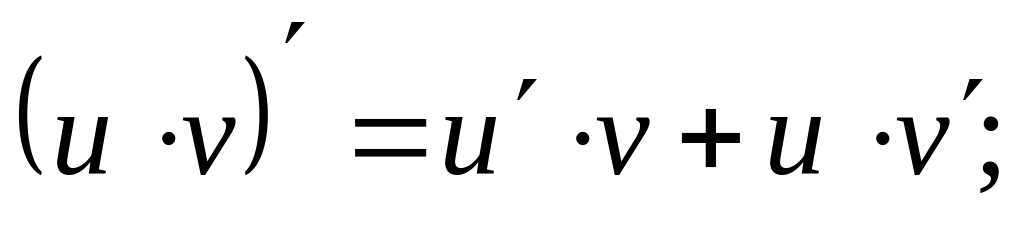
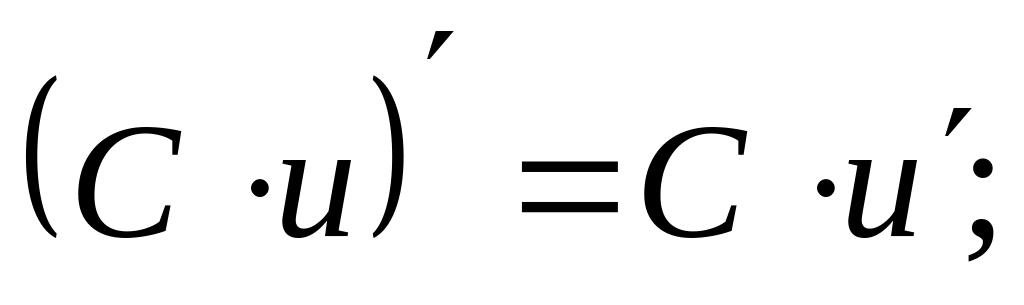

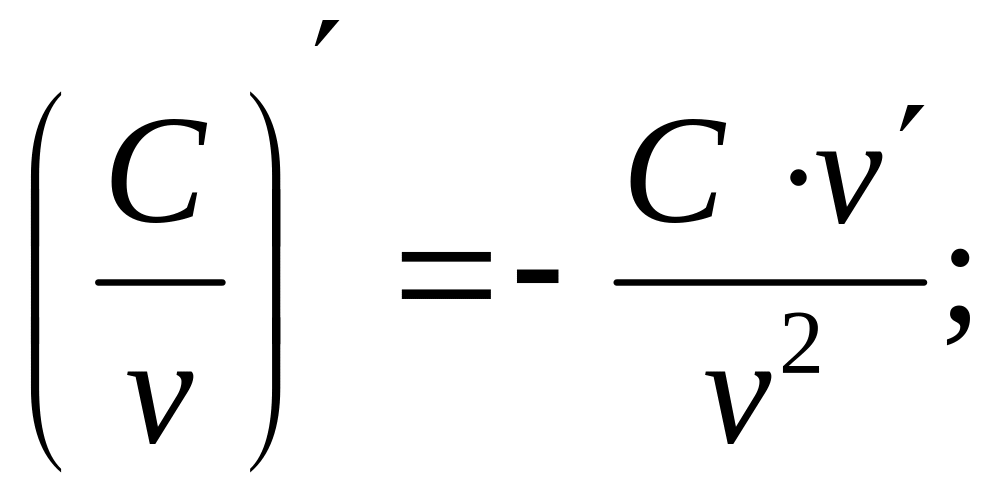
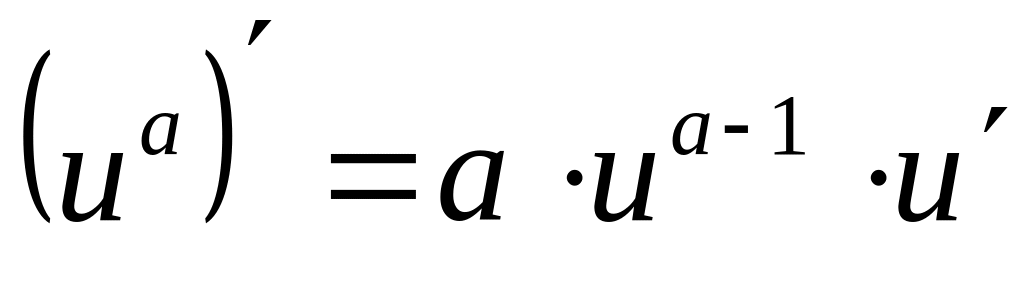 (где
а – действительное число).
(где
а – действительное число).
Производная сложной функции.
Пусть y=f(u), u=(x), где (x)и f(u) – дифференцируемые функции соответственно по аргументам х и u. Тогда y=f[(x)] – сложная функция, также дифференцируемая по аргументу х.
В других обозначениях
![]() .
.
Пример 2.
Продифференцировать следующие функции:
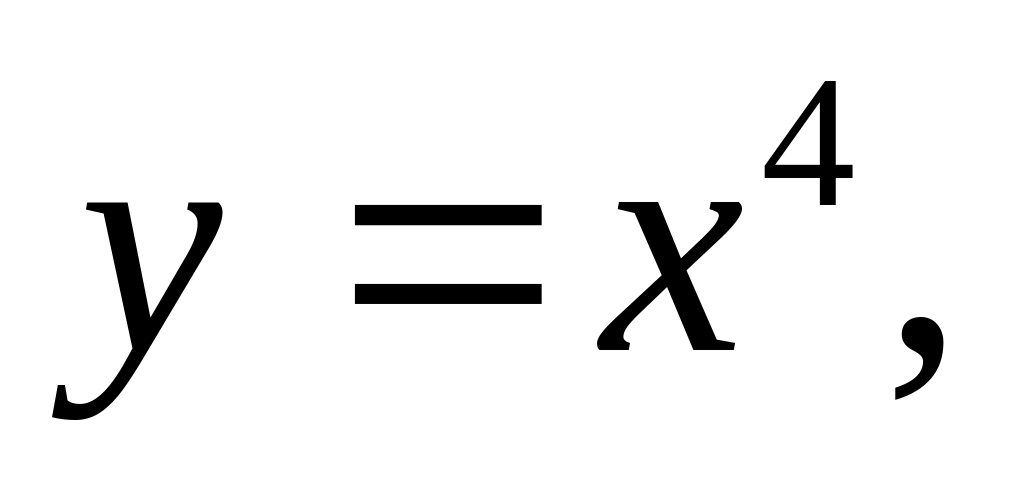 2)
2)
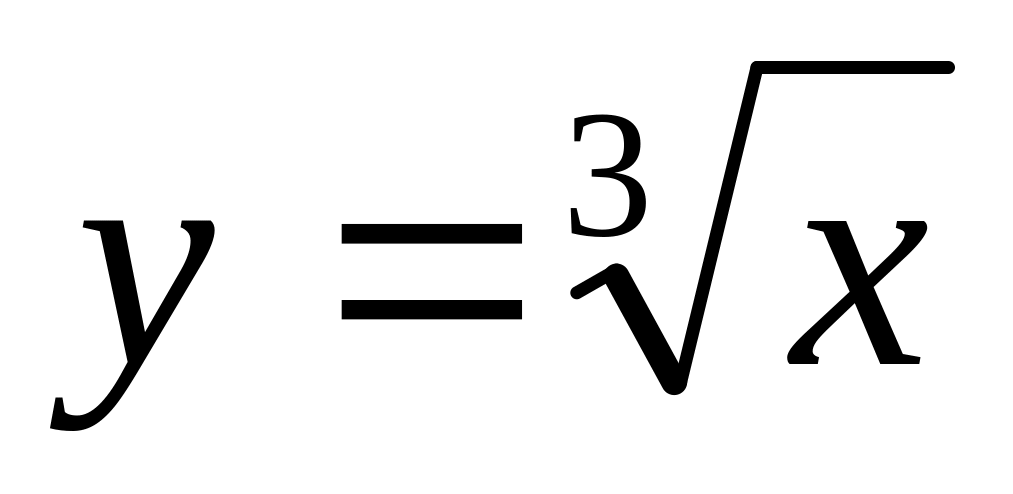 ,
3)
,
3)
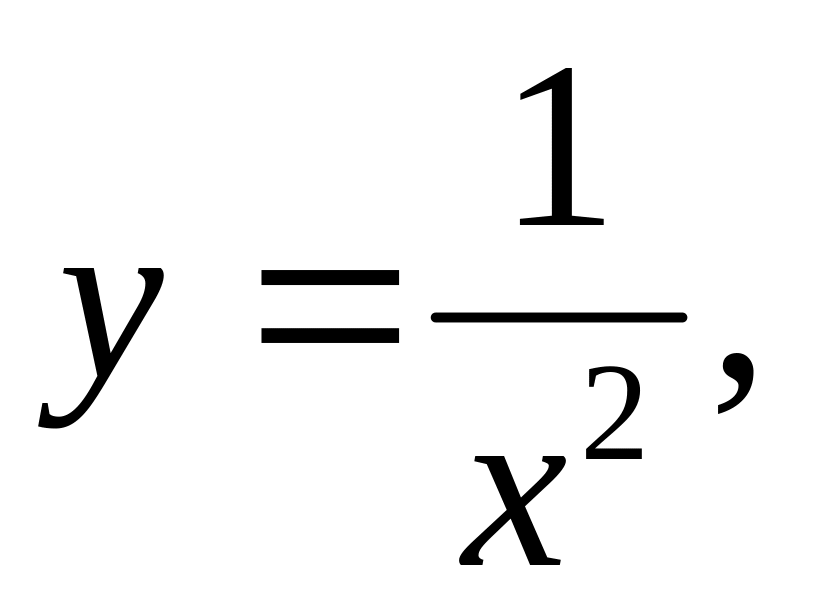 4)
4)
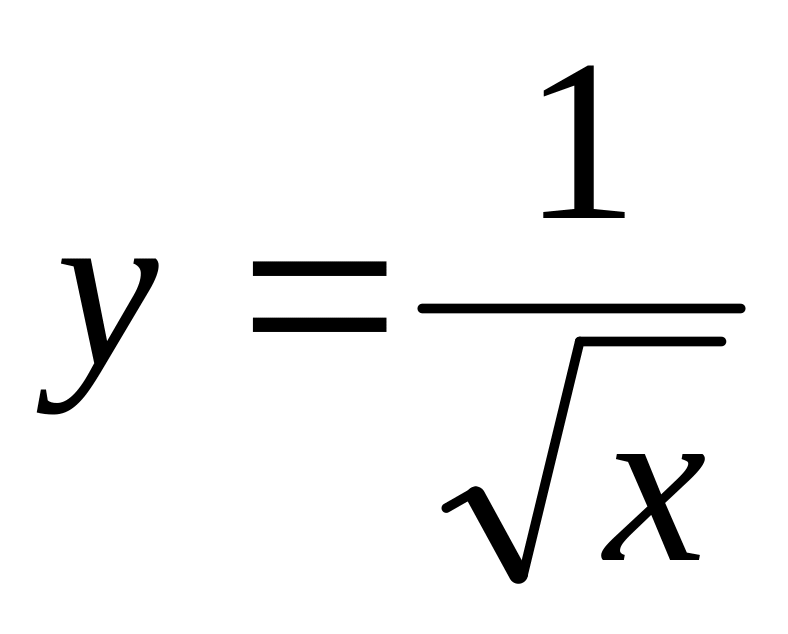 .
.
Решение.
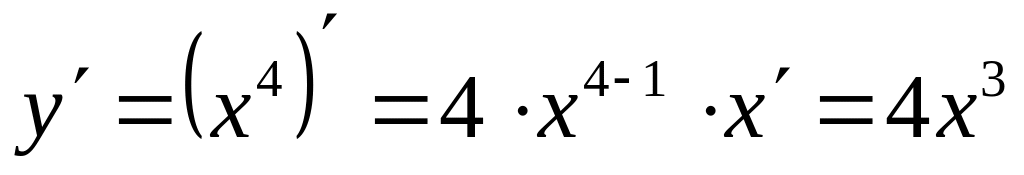 ;
;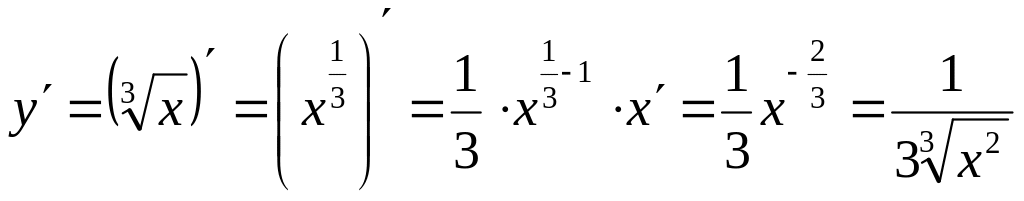 ;
;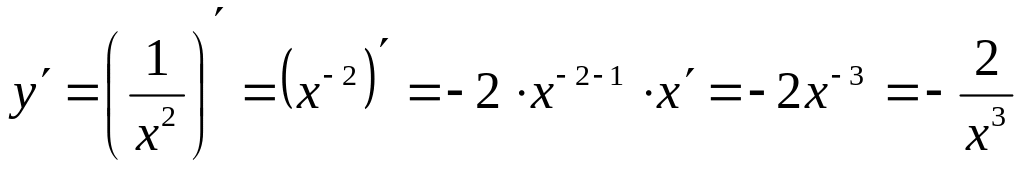 ;
;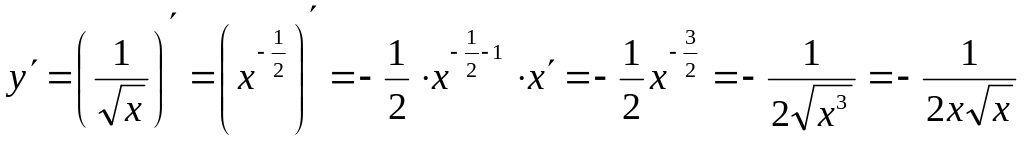 .
.
Пример 3.
Найти
производную функции
![]() .
.
Решение.
Обозначим
![]() ,
находим
,
находим
![]() .
.
Тогда
![]()
Пример 4.
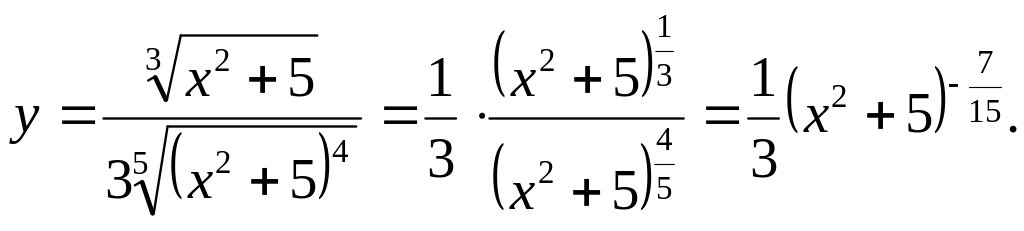
![]()
4.4. Основные формулы дифференцирования.
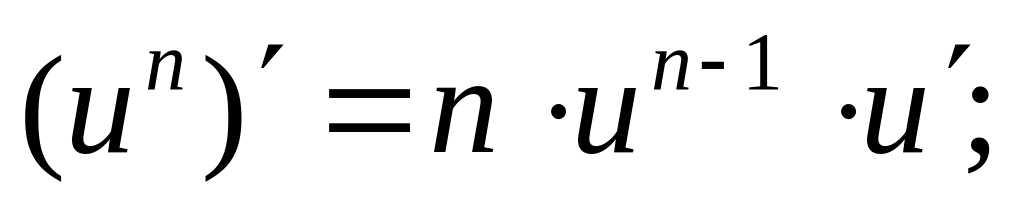
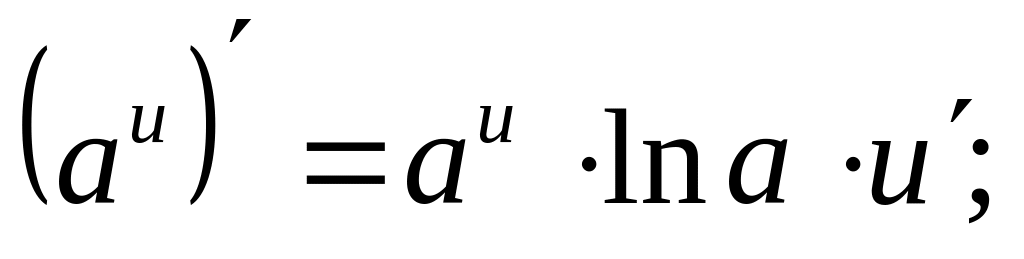
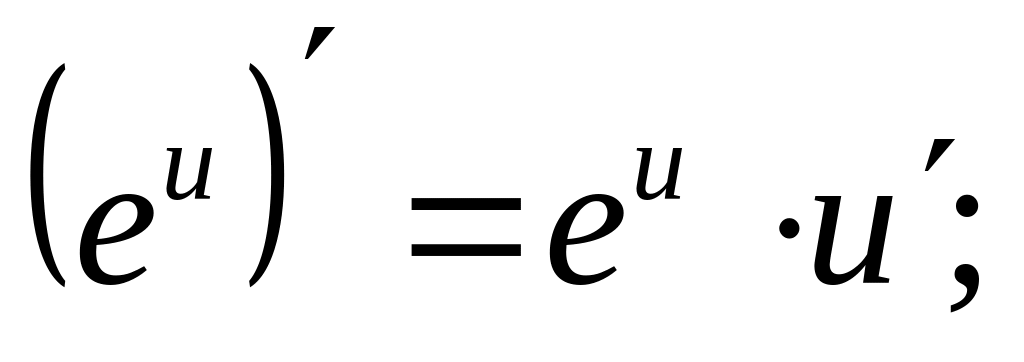
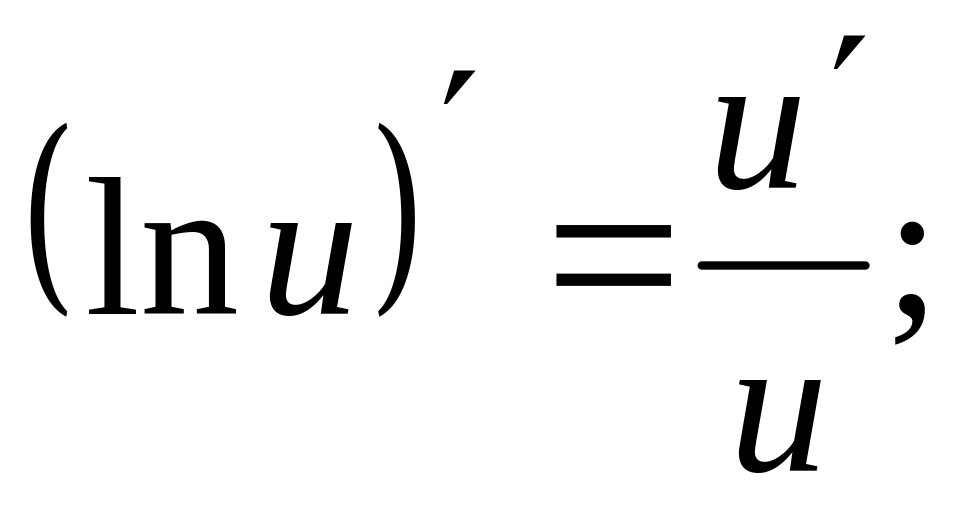
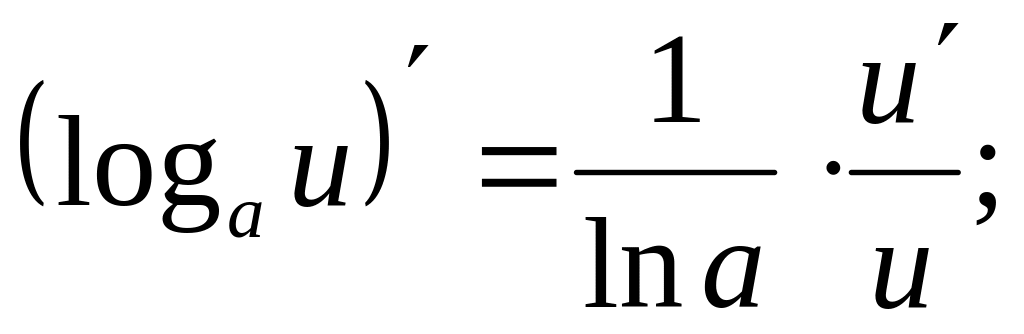
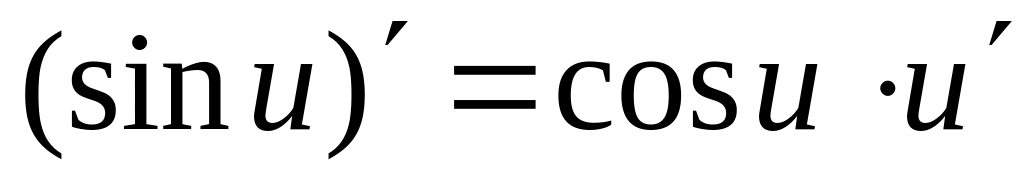 ;
;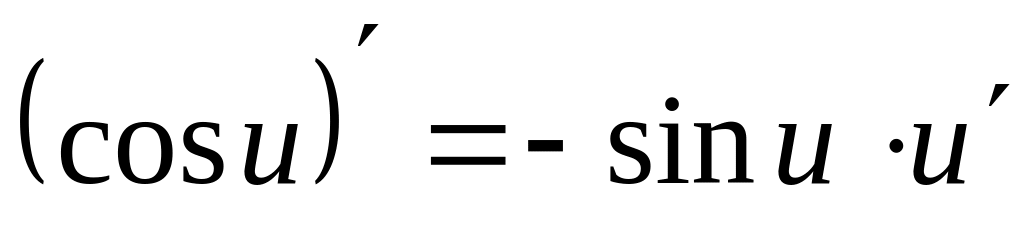 ;
;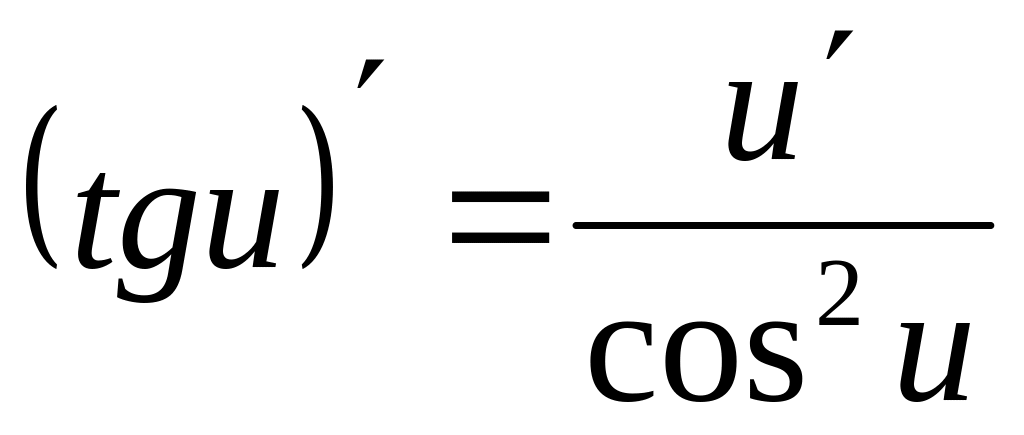 ;
;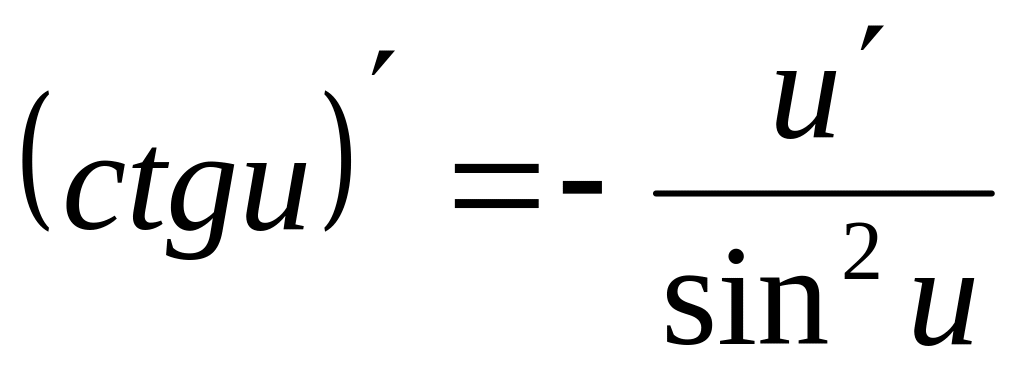 ;
;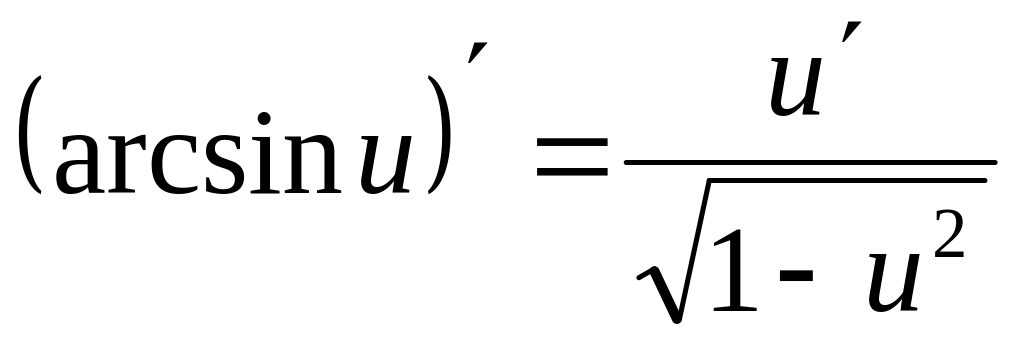 ;
; ;
;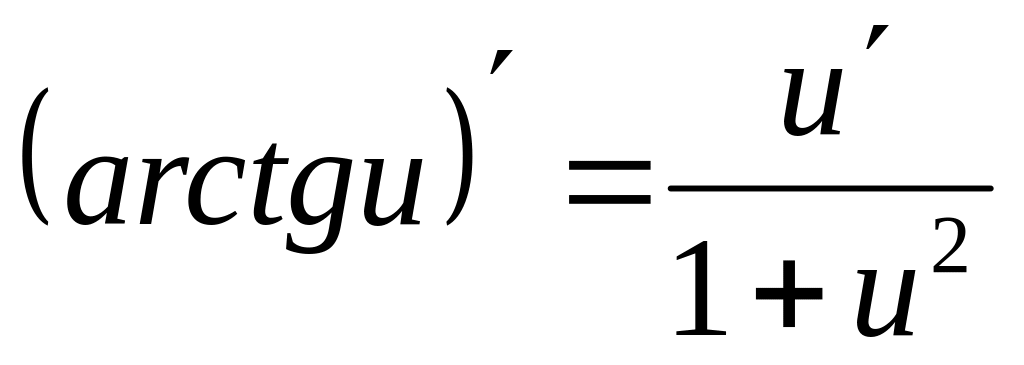 ;
;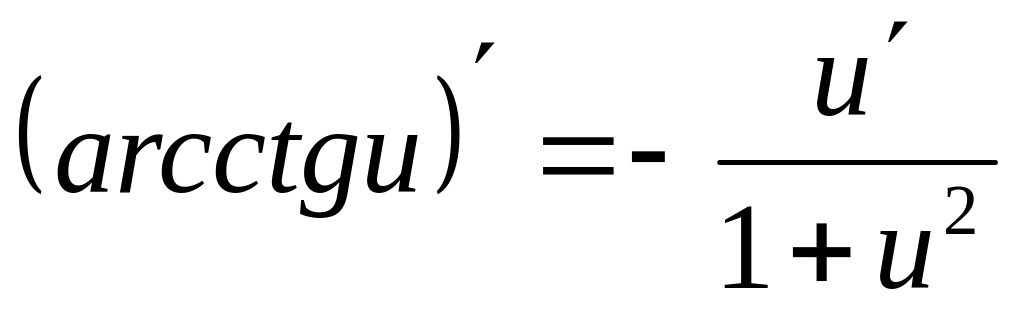 .
.
4.5. Дифференциал функции.
Определение: дифференциалом dx аргумента х называется его приращение х, т.е.
dx=x.
Дифференциалом dy функции y=f(x) называется произведение производной этой функции на дифференциал ее аргумента:
![]()
При малых х имеют место следующие приближенные формулы:
y dy;
f(x+x) f(x)+dy.
Правила нахождения дифференциалов функций аналогичны соответствующим правилам для нахождения производных:
d(C)=0;
d(uv)=dudv;
d(uv)=udv+vdu;
d(Cu)=Cdu;
d
 =
=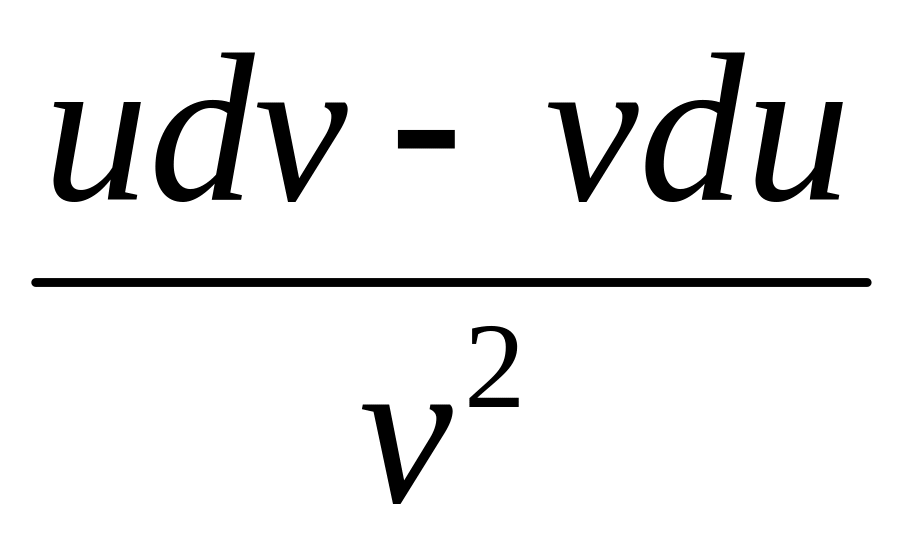 .
.
Пример 5.
Найти
дифференциал функции
![]() .
.
Решение.
![]() .
.
Пример 6.
Найти
дифференциал функции
![]()
Решение.
![]()
Пример 7.
Вычислить
значение дифференциала функции
![]() при х=2 и dx=0,1.
при х=2 и dx=0,1.
Решение.
![]()
![]()
Приближенные вычисления с помощью дифференциала.
Правило.
Если требуется вычислить значение
функции в точке
,
т.е. f(
),
и если проще вычислить значение этой
функции и ее производную в точке
(т.е. f(
)
и
),
то
при достаточно малой по абсолютному
значению разности
![]() можно заменить приращение функции ее
дифференциалом
можно заменить приращение функции ее
дифференциалом
![]() ,
,
отсюда
![]() .
.
Пример 8.
При
помощи дифференциала найти приближенное
значение функции
![]() при х=3,01.
при х=3,01.
Решение.
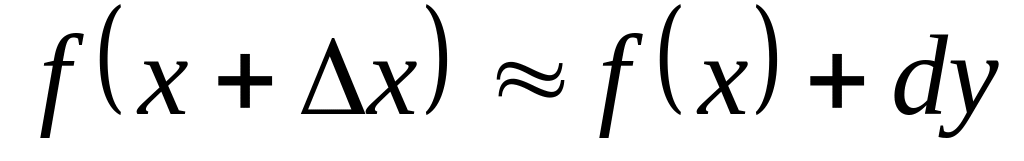 .
Пусть х=3,
.
Пусть х=3,
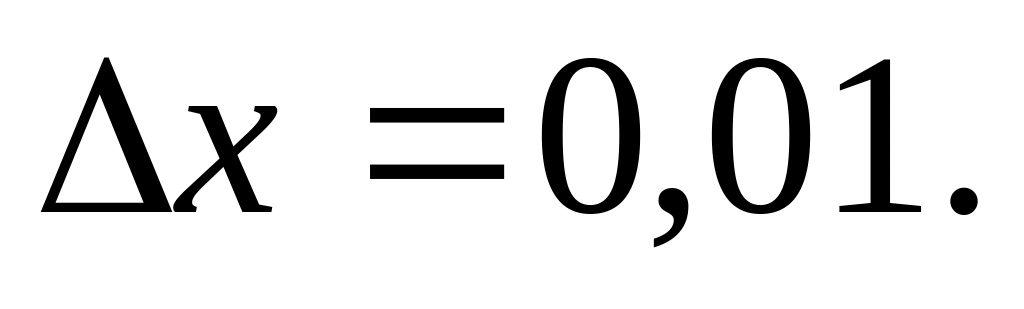 ;
;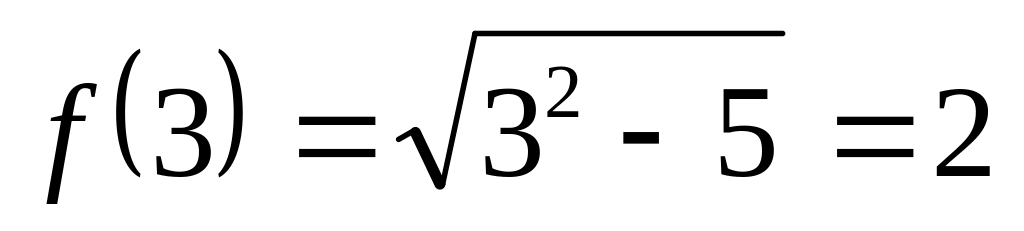 ;
;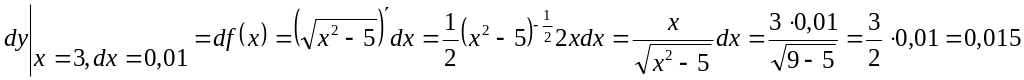
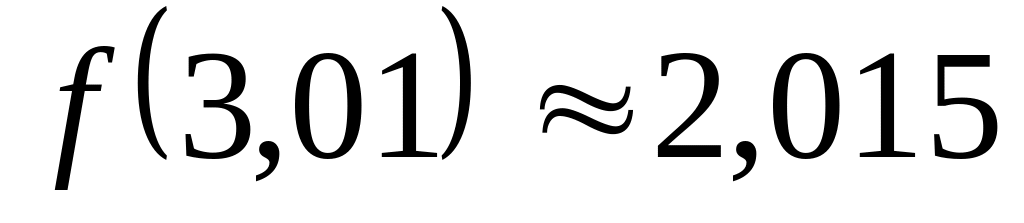 .
.
Пример 9.
Вычислить
при помощи дифференциала приближенное
значение
![]()
Решение.
можно
рассматривать как частное значение
функции
![]() при х=28.
при х=28.
Выберем ближайшее значение х при котором функция легко вычисляется. Например, при
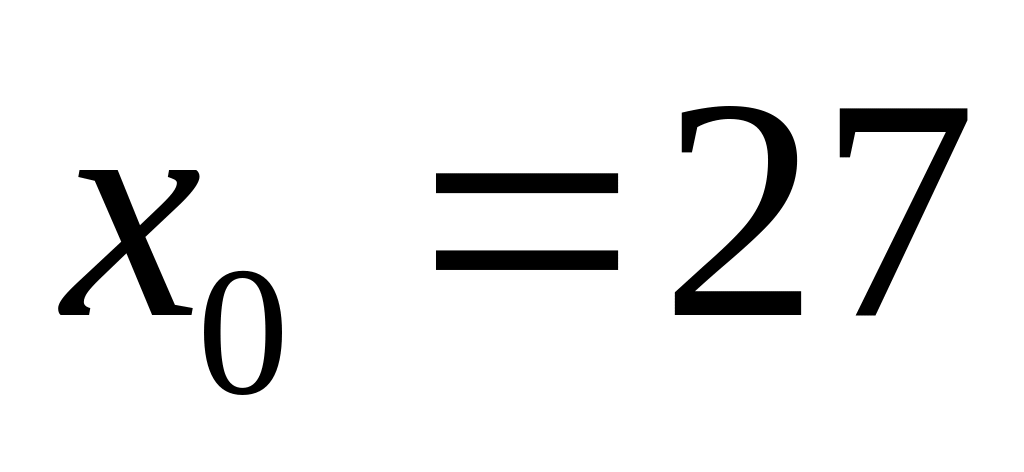
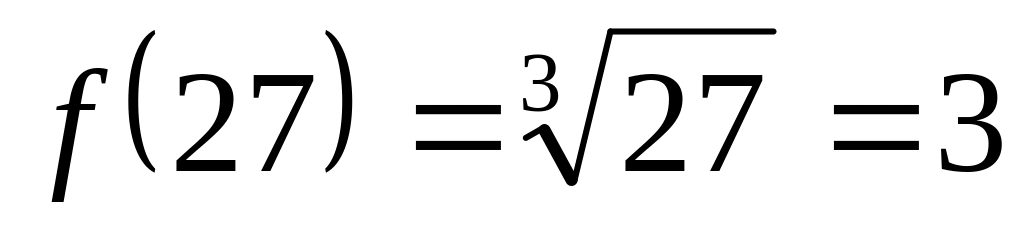 .
.Разность между рассмотренными значениями аргумента можно принять за дифференциал аргумента
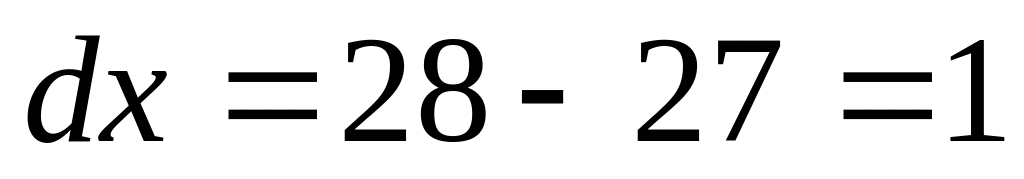 .
.Вычислим значения дифференциала функции при и dx=1.
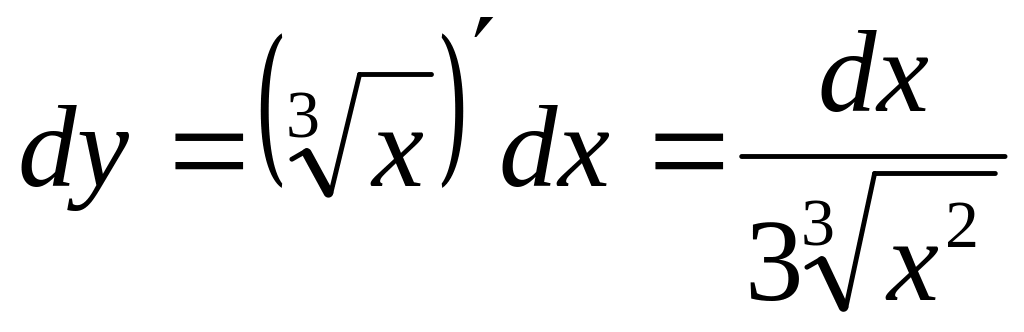 ;
;
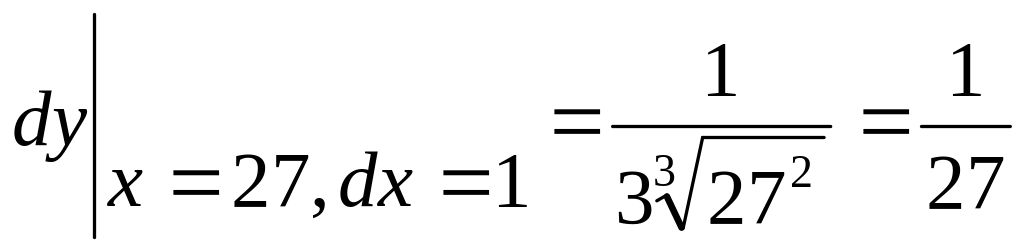 .
.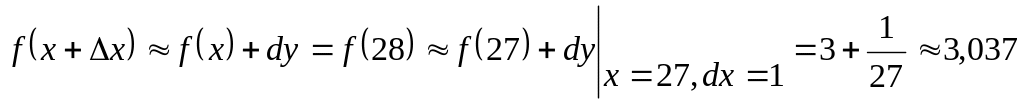 .
.
Ответ:
![]()
