
- •Математика
- •Глава 1 элементы теории множеств
- •1.1 Понятие множества.
- •1.2. Элемент и принадлежность элемента к множеству. Операции над множествами
- •1.3. Действительные числа
- •Отрезок, интервал, окрестность
- •Глава 2 начала аналитической геометрии
- •2.1. Метод координат
- •Прямоугольная система координат на плоскости
- •2.2. Уравнение линии на плоскости
- •2.3. Расстояние между двумя точками на плоскости
- •2.4. Деление направленного отрезка в заданном отношении
- •2.5. Линии первого порядка
- •2.6. Расстояние от точки до прямой
- •2.7. Взаимное расположение двух прямых на плоскости
- •2.8. Линии второго порядка
- •2.9. Решение задач
- •Глава 3. Введение в анализ. Пределы
- •3.1. Понятие функции. График функции
- •3.2. Элементарные функции и их графики
- •3.3. Предел числовой последовательности
- •3.4. Предел функции
- •3.5. Бесконечно малые и бесконечно большие величины
- •3.6. Основные теоремы о пределах
- •3.7 Вычисление пределов
- •3.8. Непрерывность функции. Точки разрыва
- •3.9. Решение задач
- •Глава 4. Дифференциальное исчисление.
- •4.1. Понятие производной.
- •4.2. Геометрический смысл производной.
- •4.4. Основные формулы дифференцирования.
- •4.5. Дифференциал функции.
- •Приближенные вычисления с помощью дифференциала.
- •4.6. Решение задач
- •Продифференцировать следующие функции
- •Глава 5. Элементы интегрального исчисления.
- •5.1. Определение интегрирования.
- •5.2. Неопределенный интеграл.
- •5.3. Таблица простейших интегралов.
- •5.4. Непосредственное интегрирование
- •5.5. Методы интегрирования
- •Метод основан на использовании формулы дифференцирования произведения двух функций. Пусть u и V дифференцируемые функции от х. Тогда
- •Глава 6. Элементы теории вероятностей
- •6.1. Предмет теории вероятностей
- •6.2. Классическое определение вероятности
- •6.3. Теоремы сложения и умножения вероятностей
- •6.4. Формула полной вероятности
- •6.5. Формулы Байеса
- •6.6.Схема Бернулли
- •6.7. Закон распределения и числовые характеристики дискретной случайной величины
- •6.8. Решение задач
3.8. Непрерывность функции. Точки разрыва
Понятие непрерывности функции, так же как и понятие предела, является одним из основных понятий математического анализа.
Определение
7. Функция
![]() называется непрерывной в точке х0,
если она удовлетворяет следующим трем
условиям: 1) определена в точке х0
(т.е. существует
называется непрерывной в точке х0,
если она удовлетворяет следующим трем
условиям: 1) определена в точке х0
(т.е. существует
![]() );
2) имеет конечный предел функции при
);
2) имеет конечный предел функции при
![]() ;
3) этот предел равен значению функции в
точке х0, т.е.
;
3) этот предел равен значению функции в
точке х0, т.е.
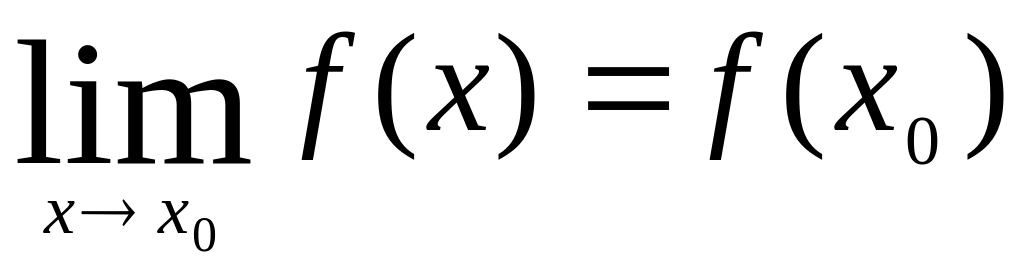 .
.
Пример. Исследовать непрерывность в точке х=0 следующих функций:
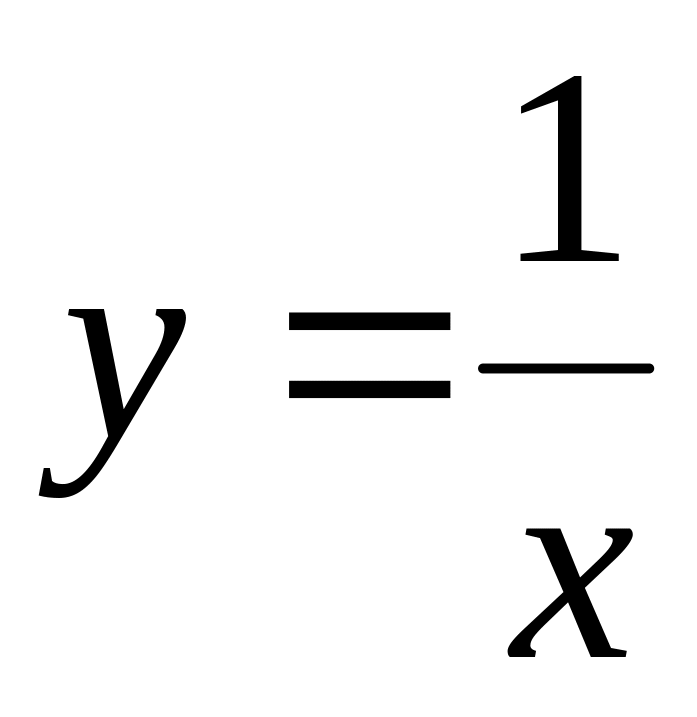 .
В точке х=0
эта функция не является непрерывной,
так как нарушено первое условие
непрерывности – существование
.
В точке х=0
эта функция не является непрерывной,
так как нарушено первое условие
непрерывности – существование
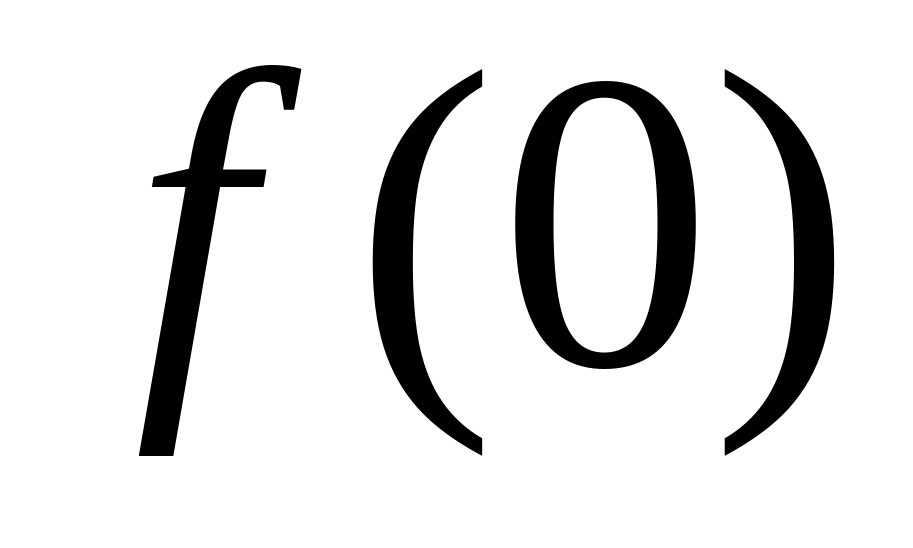 .
. В
точке х=0
функция не является непрерывной,
несмотря на то, что выполнено первое
условие (
В
точке х=0
функция не является непрерывной,
несмотря на то, что выполнено первое
условие (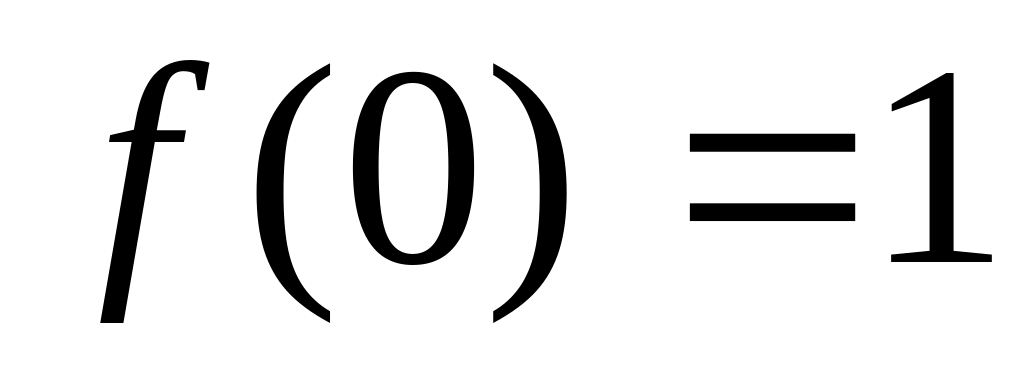 ).
Нарушено второе условие – отсутствует
).
Нарушено второе условие – отсутствует
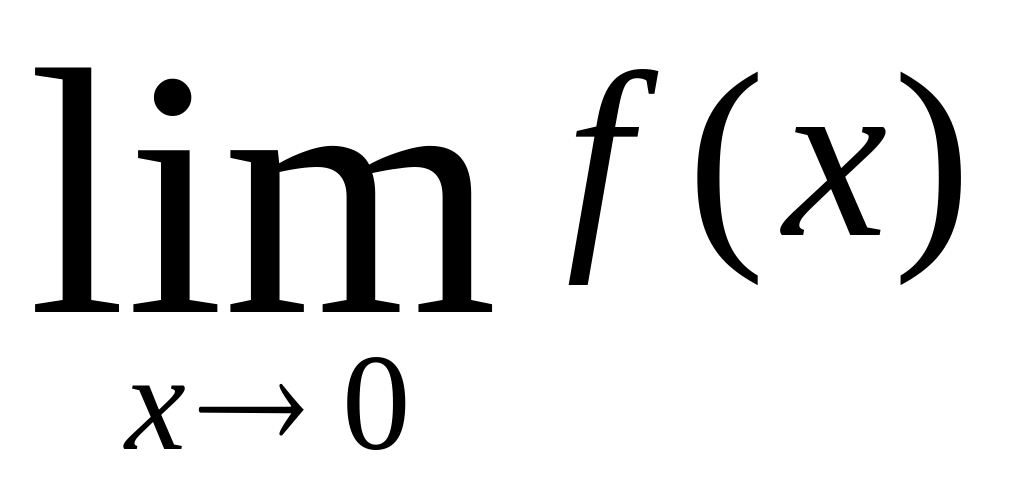 (точнее говоря, существуют односторонние
пределы слева и справа, не равные друг
другу, но общего предела не существует).
(точнее говоря, существуют односторонние
пределы слева и справа, не равные друг
другу, но общего предела не существует).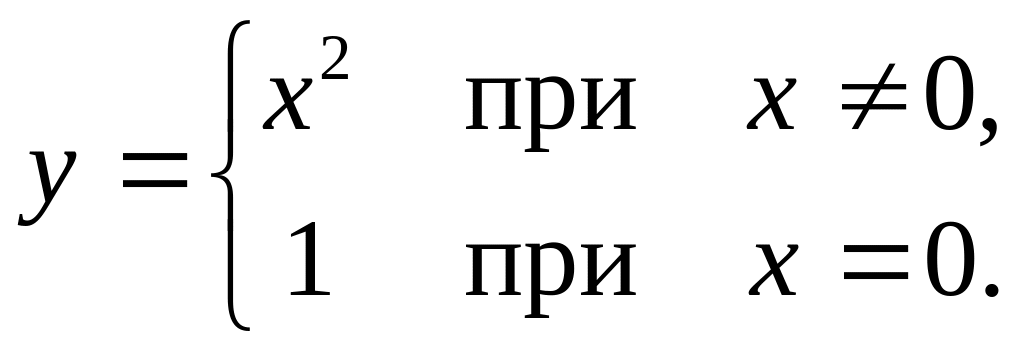 Первые
два условия непрерывности выполнены,
но нарушено третье основное условие:
Первые
два условия непрерывности выполнены,
но нарушено третье основное условие:
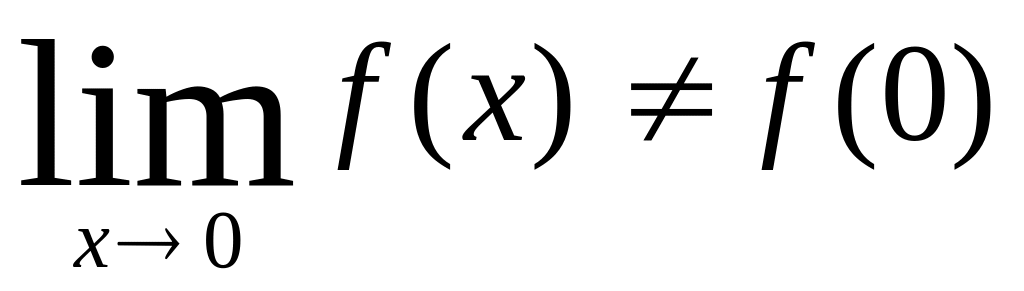
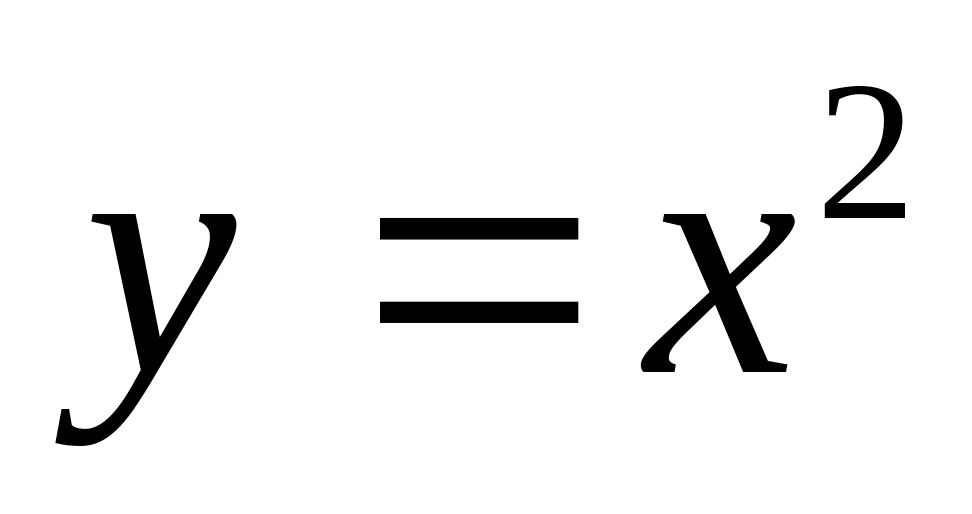 .
Все три условия
непрерывности выполнены. Эта функция
непрерывна в точке х=0.
.
Все три условия
непрерывности выполнены. Эта функция
непрерывна в точке х=0.
Определение непрерывности функции в точке может быть записано и так:
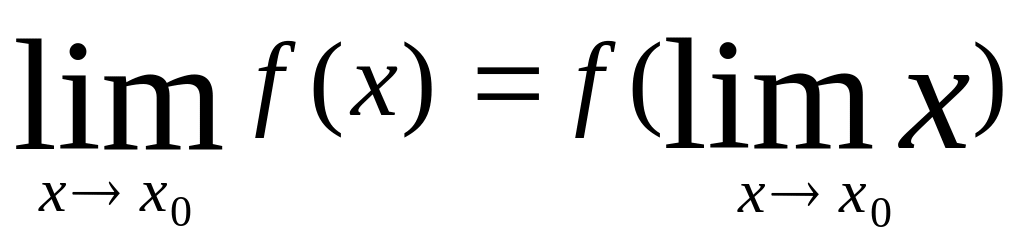 ,
,
т.е. для непрерывной функции возможна перестановка символов предела и функции.
Если функция непрерывна в каждой точке интервала (а; в), то она называется непрерывной на этом интервале.
Точка
![]() называется точкой разрыва функции,
если эта функция в данной точке не
является непрерывной. Различают точки
разрыва: первого рода (когда существуют
конечные односторонние пределы слева
и справа, не равные друг другу) и второго
рода (когда хотя бы один из односторонних
пределов слева и справа равен бесконечности
или не существует).Так, в рассмотренном
выше примере в п.2 точка
=0
является разрывом первого рода, а в п.1.
– разрывом второго рода. К точкам разрыва
первого рода относятся так же точки
устранимого разрыва, когда предел
функции при
существует, но не равен значению функции
в этой точке. Так, точка
=0
в п.3. примера является точкой устранимого
разрыва.
называется точкой разрыва функции,
если эта функция в данной точке не
является непрерывной. Различают точки
разрыва: первого рода (когда существуют
конечные односторонние пределы слева
и справа, не равные друг другу) и второго
рода (когда хотя бы один из односторонних
пределов слева и справа равен бесконечности
или не существует).Так, в рассмотренном
выше примере в п.2 точка
=0
является разрывом первого рода, а в п.1.
– разрывом второго рода. К точкам разрыва
первого рода относятся так же точки
устранимого разрыва, когда предел
функции при
существует, но не равен значению функции
в этой точке. Так, точка
=0
в п.3. примера является точкой устранимого
разрыва.![]()
3.9. Решение задач
Задача 31.
Исследуйте непрерывность следующих функций:
а)
![]() в точках х=1 и х=-1.
в точках х=1 и х=-1.
б)
![]() в точках х=0, х=-1, х=1.
в точках х=0, х=-1, х=1.
в)
![]() в точках х=-2, х=0, х=1.
в точках х=-2, х=0, х=1.
г)
![]() в точках х=-2, х=0, х=5.
в точках х=-2, х=0, х=5.
д)
![]() в точках х=-1, х=0, х=3.
в точках х=-1, х=0, х=3.
е)
![]() в точках х=-2, х=0, х=2.
в точках х=-2, х=0, х=2.
Задача 32.
Доказать
непрерывность функции
![]() в
точке х=0 или установить характер разрыва:
в
точке х=0 или установить характер разрыва:
а)
![]() ;
б)
;
б)
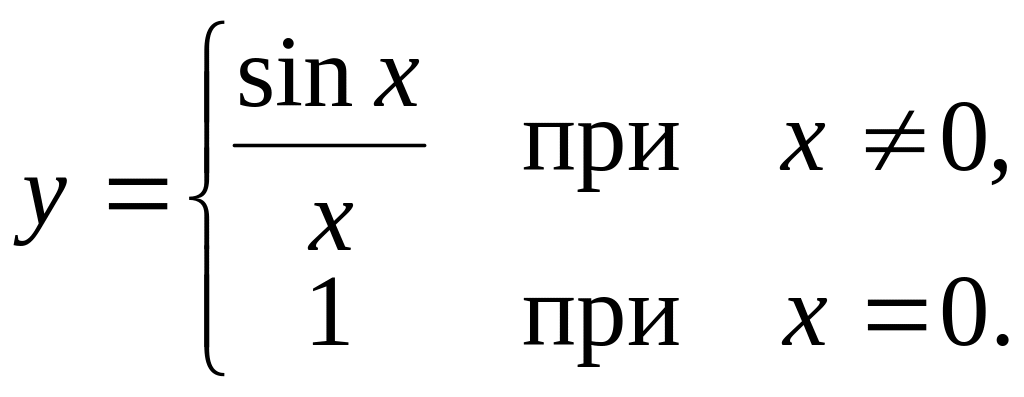
в)
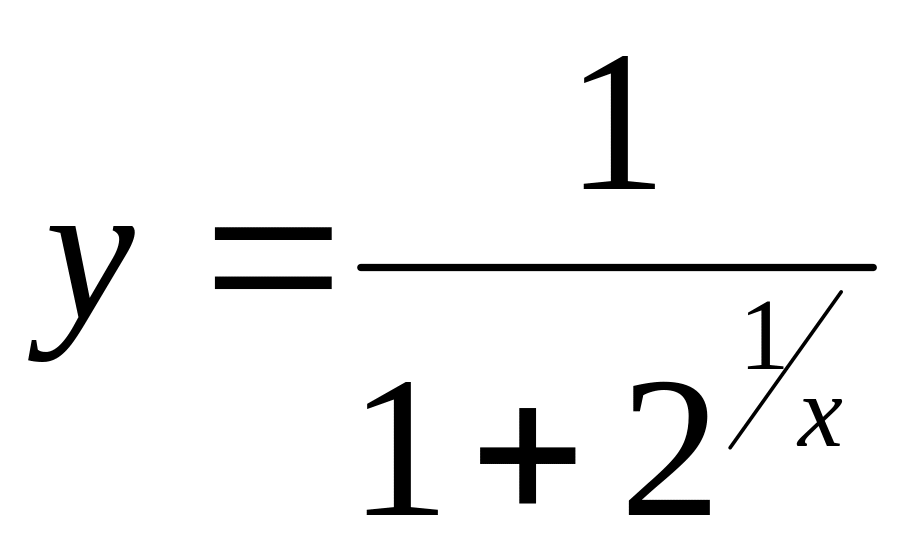 ;
г)
;
г)
![]() .
.
Задача 33.
Какие из данных функций являются непрерывными в точке х=1? В случае нарушения непрерывности установить характер точки разрыва.
а)
![]() ;
б)
;
б)
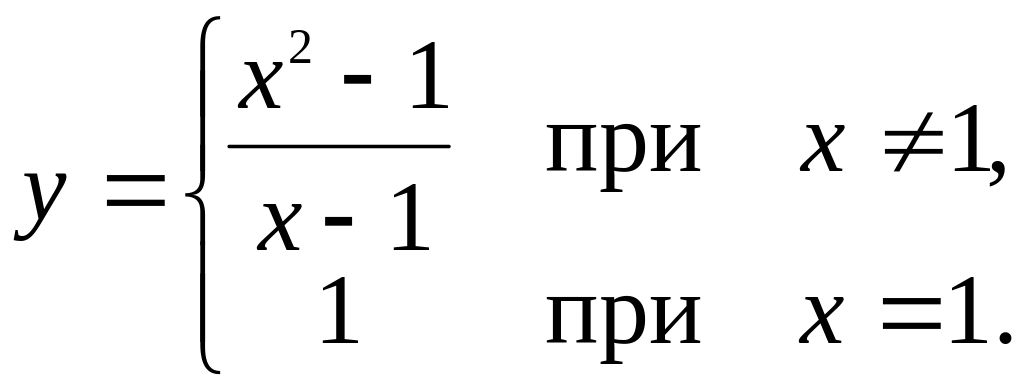
в)
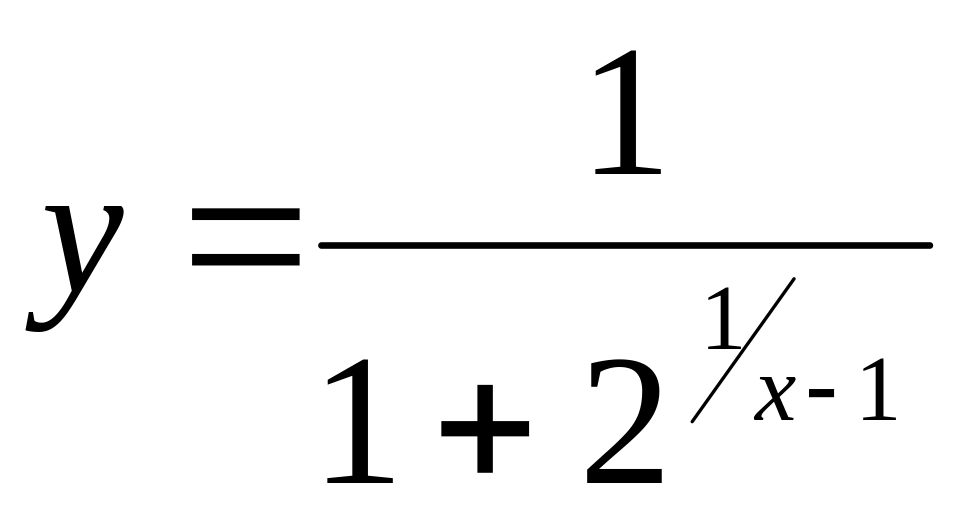 ;
г)
;
г)
![]() .
.
Глава 4. Дифференциальное исчисление.
4.1. Понятие производной.
Пусть
на интервале (a,b)
задана функция f(x).
Возьмем произвольно точку
![]() Тогда для любой точки
Тогда для любой точки
![]() разность
разность
![]() называется приращением аргумента
х в точке
называется приращением аргумента
х в точке
![]() и обозначается
и обозначается
![]() ,
,
откуда
![]() .
.
Разность
![]() называется приращением функции f(x)
в точке
и обозначается
называется приращением функции f(x)
в точке
и обозначается
![]() .
.
Т.е.
![]() ,
,
или
![]() .
.
Определение.
Производной функции у=f(x)
в точке
называется предел отношения приращения
функции
к приращению аргумента х
при условии, что х0,
а указанный предел существует. Символически
производная обозначается
![]() .
.
Конкретным значениям соответствуют определенные значения производной, если она существует приданных х. Следовательно производная является функцией аргумента х и обозначается любым из равноправных символов:
![]() («игрек
штрих»),
(«игрек
штрих»),
![]() («эф
штрих от икс»),
(«эф
штрих от икс»),
![]() («дэ
игрек по дэ икс»).
(«дэ
игрек по дэ икс»).
Итак,
![]() .
.
Операция нахождения производной называется дифференцированием функции.
Правило. Для нахождения производной функции y=f(x) по аргументу х на основе определения нужно найти:
наращенное значение функции у+у;
приращение функции у;
отношение приращения функции к приращению аргумента
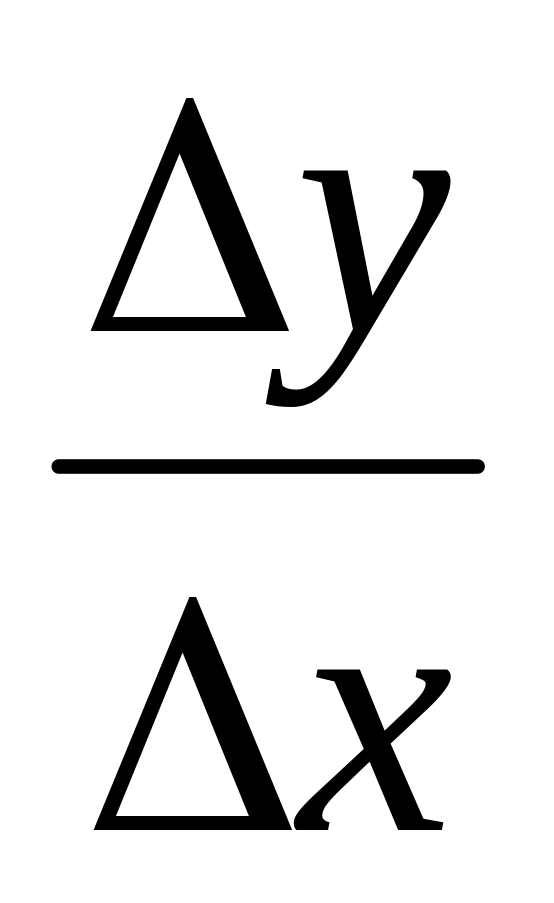 ;
;
предел
этого отношения при х0
![]() .
.
Пример 1.
Вычислением
![]() найти производную функции
найти производную функции
![]() .
.
Решение.
Воспользуемся правилом нахождения производной.
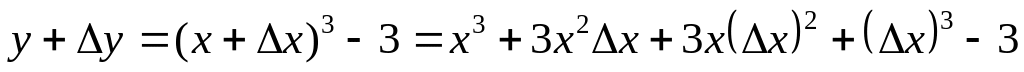 ;
;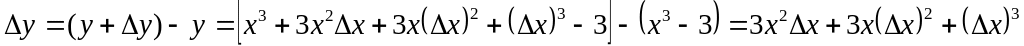 ;
;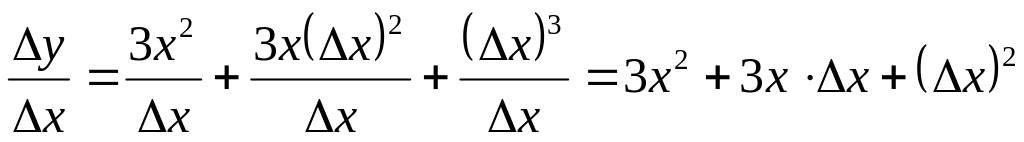 ;
;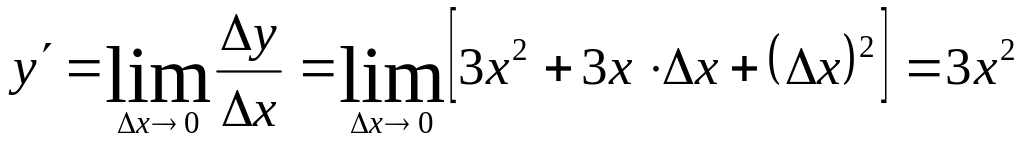 .
.
