МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО

ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ЭКОНОМИКИ И УПРАВЛЕНИЯ

Математика

Учебное пособие

для студентов бизнес-колледжа

Новосибирск 2002

Рассмотрено и одобрено на

Заседании кафедры высшей математики.

Протокол № от .

Составитель:

старший преподаватель И.В. Фролова.

Глава 1 элементы теории множеств

1.1 Понятие множества.

Понятие множества является одним из основных в математике. Оно относится к так называемым первичным, неопределяемым, понятиям. Смысл этого понятия становится ясным из примеров.

Пример 1.

1. Множество студентов на данной лекции по высшей математике.

2. Множество юношей, присутствующих на занятиях 5 сентября.

3. Множество сельхозпредприятий в Новосибирской области.

4. Множество экономистов, работающих по специальности в г. Новосибирске и т.д.

Таким образом понятие множества можно отнести ко всем однородным объектам (множество листьев на деревьях, множество песчинок в 1 песчаного грунта и т.д.).

Синонимами слова «множество» являются : совокупность, набор, система,…

Объекты, из которых состоит множество, называются элементами множества.

Для сокращения записи и придания строгости и однозначности утверждений, предложений (теорем) в математике широко используются специальные символы:

 — любой, всякий, каждый (символ всеобщности);

  существует, найдется;

  такое, что; иногда используют символ [];

  принадлежность множеству;

  не принадлежит множеству;

  содержится, включено (строгое включение);

  не включено;

  следует;

  тогда и только тогда ( равносильность);

{…}  множество, элементы которого можно перечислить;

[…]  множество неперечислимое, включающее крайние границы (интервал);

(…)  множество неперечислимое, не включающее границы (интервал);

  или (символ объединения множеств);

  и (символ пересечения множеств);

  деление;

\  разность;

  конец доказательства;

 читается «модуль а».

1.2. Элемент и принадлежность элемента к множеству. Операции над множествами

Множества принято обозначать заглавными (прописными) буквами латинского алфавита ( А, В, С, …).

Элементы множества обозначают строчными (малыми) буквами латинского алфавита (а, b, с,…).

Пример 2.

Пусть А – множество студентов в группе:

а – Иванов,

b – Петров,

c – Сидоров,

. . . . . . . . . . .

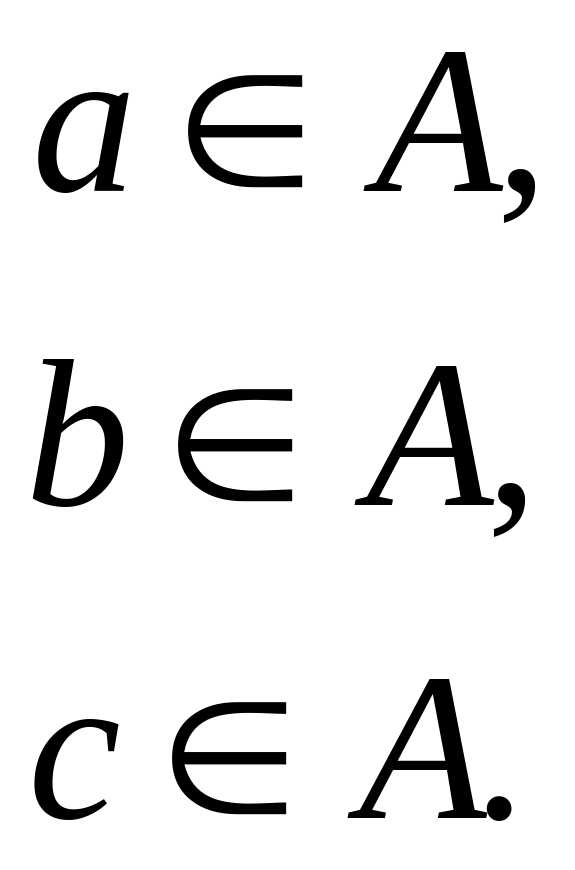
Чтобы запись была компактнее, используют индексы:

. . . . . . . . . . или

или

Если элемент а не принадлежит множеству А, то пишут

Способы задания множеств бывают различны.

Пример 3.

Пусть А – множество целых положительных чисел, не превышающих 10. Тогда множество А можно представить следующим образом:

Способ 1: А={1,2,3,4,5,6,7,8,9,10}. Описание путем перечисления всех элементов.

Способ 2: А={x| 0<x 10, x- целое}.

Часто требуется при описании множества указывать свойства, которыми обладают элементы этого множества. В предыдущем примере таким свойством было «х- целые числа». То есть, если F(x)- какое-то свойство числа х, тогда запись {x|F(x)} означает, что все элементы множества обладают свойством F(x).

Пример 4.

Пусть F(x) есть корни уравнения . Тогда запишем А={x| }, т.е. это означает, что данное множество А есть совокупность корней уравнения (корнями являются числа ). Таким образом, А есть множество, состоящее только из двух чисел.

Если множество не содержит ни одного элемента, то пишут , т.е. если А=, то А – пустое множество. (Аналогично числу нуль.)

Пример 5.

Пусть А – множество студентов 1 курса бизнес-колледжа, В – множество девушек. Тогда ВА (В включено в А). Т.е. В есть подмножество множества А.

Множества А и В называются равными, если они состоят из одних и тех же элементов. Запись: А=В, если АВ и ВА.

Пример 6.

А={3,4,5,6}; B={4,6,5,3}.

Из определения равенств множеств вытекает, что порядок элементов в множестве несущественен.

Любые действия над множествами называются операциями. Результатом операции является другое множество.

Операции над множествами:

1) Объединением (суммой) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В, т.е. принадлежат А или принадлежат В. Объединение обозначается следующим образом

А В

АВ={x|xA или  хВ} (1.1)

(1.1)

Пример 7.

Если А={1,2,3,4} и В={2,4,5,6}, то

АВ={1,2,3,4,5,6,7}.

2) Пересечением (произведением) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. Обозначается АВ.

АВ={x|xA и xB} (1.2)

Пример 8.

Пусть А={1,2,3,4}, B={2,4,5,6,7}, то

АВ={2,4} или АВ={2,4}.

Множества называются непересекающимися, если они не имеют общих элементов, т.е. если

АВ=.

Пример 9.

Пусть A={1,2,3}, B={4,5,6}. Тогда АВ=.

3) Разность множеств. Данная операция обозначается А\В. Разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат А и не принадлежат В.

А\B={x| xА, xВ} (1.3)

B \A={x| xB, xA} (1.4)

Пример 10.

Пусть А={1,2,3,4}, B={2,4,6,7}, тогда

А\B={1,3}, B\A={6,7}.

Универсальное множество (I)- это множество, которое содержит все элементы, из которых может состоять множество А. Любое множество А полностью содержится в множестве I, т.е.

АI=А (1.5) Универсальное множество называют иногда полным или единичным. Универсальное множество удобно изображать в виде точек прямоугольника. Отдельные области внутри этого прямоугольника будут означать различные подмножества универсального множества.

- подмножества

универсального множества I,

т.е.

Изображение множеств в виде областей в прямоугольнике, представляющим универсальное множество, называется диаграммой Эйлера-Венна.

Дополнение множества. Множество , определяемое из соотношения

(1.6) называется дополнением множества А (до универсального множества I).

I

Пример 12.

Пусть I={1,2,3,4,5,6,7} и A={3,4,5}, тогда ={1,2,6,7}.

Из формулы (1.6) следует, что А и не имеют общих элементов, т.е.

(1.7) кроме того

(1.8) т.е. в I не имеется элементов, которые не принадлежали бы ни к А ни к . Из формулы (1.8) следует, что

(1.9) Двойное отрицание есть А. (Читается: дополнение дополнения А есть А.)