
9). Равен
Варианты ответов: |
|||
1) |
0 |
2) |
2 |
3) |
|
4) |
6 |
10).
Число А называется пределом функции
y=f(x)
в точке x0
если для любого положительного числа
ε найдется такое положительное число
δ, что для всех x≠x0,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
Варианты ответов: |
|||
1) |
|
2) |
|
3) |
|
4) |
|
12). Равен
Варианты ответов: |
|||
1) |
1,44 |
2) |
0,6 |
3) |
1,2 |
4) |
0,72 |
13). Бесконечно малые функции α и β называются эквивалентными, если
Варианты ответов: |
|||
1) |
|
2) |
|
3) |
|
4) |
|
14). Равен
Варианты ответов: |
|||
1) |
7/8 |
2) |
5/9 |
3) |
0 |
4) |
|
16). В какой из формул эквивалентностей допущена ошибка?
Варианты ответов: |
|||
1) |
|
2) |
|
3) |
tg x ~ x2 |
4) |
Sinx ~ x |
18). Равен
Варианты ответов: |
|||
1) |
0 |
2) |
1,25 |
3) |
0,625 |
4) |
∞ |
20). Равен
Варианты ответов: |
|||
1) |
0 |
2) |
1 |
3) |
|
4) |
-0,75 |
Тест по теме «Аналитическая геометрия»
Уравнение прямой, проходящей через точки А(-1,3) и В(4,5), имеет вид
А) 3х-5у+16=0; В) 2х-5у+17=0; |
С) 2х-7у+13=0; D) 4х-5у+17=0. |
Расстояние между точками А(2,3) и В(5,7) равно
A) 7; B) 17; |
C) 5; D) 25. |
Точка С, лежащая на одной прямой с точками А(-6,-6) и В(-3,-1 ) имеет абсциссу, равную 3. Ордината точки С равна
А) y=2; В) y=5; |
С) y=9; D) y=7. |
Уравнение прямой, проходящей через начало координат и составляющей с осью ОХ угол
 имеет вид
имеет вид
A)
B)
|
C)
D)
|
Угол между прямыми 3x-4y=6 и 8x+6y=11 равен
A)
B)
|
C)
D)
|
Среди прямых
1) 3x-2y+7=0; 2) 6x-4y-9=0; 3) 6x+4y-5=0; 4) 2x+3y-6=0 укажите параллельные.
A) 1 и 2; B) 1 и 3; |
C) 1 и 4; D) 2 и 3. |
Точка А(-2,3) лежит на искомой прямой, перпендикулярной к 2х-3у+8=0. Уравнение этой прямой имеет вид
А) 3х+2у=0; В) 5x-5y=2; |
С) 7x+3y=1; D) 4x+6y=2. |
Уравнение прямой, проходящей через начало координат и точку пересечения прямых 2х+5у-8=0 и 3х+3у+4=0 имеет вид
А) 6y+8z=0; В) y+7z=0; |
С) 6y+11у=0; D) y+5z=0. |
Какие из уравнений являются уравнениями прямой?
1) x+2y-5=0;
2)
![]() ;
3) xy-4=0;
4) y=4-x;
5)
;
3) xy-4=0;
4) y=4-x;
5)
![]() .
.
A) 1 и 2; B) 3 и 4; |
C) 1 и 5; D) 1 и 4. |
Уравнение плоскости, проходящей через ось Ох и точку А(2;5;-1) имеет вид
А) 6y+8z=0; В) y+7z=0; |
С) 3y+5z=0; D) y+5z=0. |
Уравнение плоскости, проходящей через точки А(2,5,-1) В(-3,1,3) параллельно оси Оу имеет вид
А) 6y+8z=0; В) 4х+5z=3; |
С) 3y+5z=0; D) y+5z=0. |
Уравнение плоскости, проходящей через точки А(1,1,0), В(2,-1,-1) перпендикулярно к плоскости 5х+2у+3z-7=0 имеет вид
А) x+6y+8z=0; В) 4х+5z=3; |
С) x+2y-3z=3; D) 3x- y+5z=5. |
Какой геометрический смысл имеют числа 2, -3, 5 в уравнении плоскости 2x-3y+5z=30?
A) Координаты точки, принадлежащей плоскости; B) Координаты вектора, лежащего на плоскости; |
C) Координаты вектора, перпендикулярного плоскости; D) Координаты точки, симметричной началу координат относительно данной плоскости. |
Уравнение плоскости, проходящей через точку К(2,-5,3) параллельно плоскости 0xz имеет вид
A) 3x-5=0; B) 2x-6=0; |
C) x+5=0; D) y+5=0. |
Координаты проекции точки М(4,-3,1) на плоскость х-2у-z-15=0:
А) М1 (4,-5,0); В) М1 (5,-5,0); |
С) М1 (5,-1,0); D) М1 (3,-5,0). |
Укажите положение плоскости Ax+By=0 в трехмерном пространстве.
A) Плоскость перпендикулярна оси ОХ; B) Плоскость проходит через ось ОZ; |
C) Плоскость параллельна оси ОZ; D) Плоскость параллельна оси ОY. |
Полюс полярной системы координат совмещен с началом декартовой системы координат, а полярная ось совпадает с положительной полуосью абсцисс. Тогда точка
 ,
заданная в декартовой системе координат,
имеет полярный радиус
,
заданная в декартовой системе координат,
имеет полярный радиус
 при
y, равном …
при
y, равном …
A)
B)
|
C) 2; D) 8. |
Полуоси эллипса
 равны
равны
|
|
Каноническое уравнение эллипса при b=15 – малой полуоси и F(-10,0) – фокусе, примет вид
А)
В)
|
С)
D)
|
Полуоси гиперболы
 равны
равны
|
|
Каноническое уравнение гиперболы при b=2- мнимой полуоси и фокусе F(-13,0) примет вид
А)
В)
|
С)
D)
|
Фокус параболы
 имеет координаты
имеет координаты
A) (6, 0); B) (-6, 0); |
C) (0,6); D) (0,-6). |
Уравнение окружности с центром в точке (-4;7) и радиусом 7 имеет вид
A)
B)
|
C)
D)
|
Поверхность, определяемая уравнением
 ,
есть
,
есть
A) сфера; B) эллипсоид вращения; |
C) эллиптический цилиндр; D) трехосный эллипсоид. |
Поверхность, определяемая уравнением
 ,
есть
,
есть
A) параболоид вращения; B) двуполостный гиперболоид; |
C) однополостный гиперболоид; D) круговой цилиндр. |
Векторная алгебра |
|
ЗАДАНИЕ № 5. Даны
точки
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 6. Даны
векторы
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 7. Даны
векторы
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 8. (выберите несколько вариантов ответа) Для смешанного произведения трех векторов верны следующие утверждения: |
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 5. Даны
векторы
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 6. Даны векторы и . Тогда скалярное произведение между данными векторами равно: |
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 7. Длина
вектора
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 8. Векторным
произведение двух векторов
|
ВАРИАНТЫ ОТВЕТОВ:
|
Производные |
|
ЗАДАНИЕ № 22. Установите
соответствие между функциями и их
производными
1.
|
ВАРИАНТЫ ОТВЕТОВ: 1.
3.
5.
|
ЗАДАНИЕ № 23. Правило
нахождения производной произведения:
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 24. Необходимым
условием существования экстремума
функции
|
ВАРИАНТЫ ОТВЕТОВ: 1.
2.
3.
4.
5. другой ответ |
ЗАДАНИЕ № 21. Наименьшее
значение функции
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 22. (выберите несколько вариантов ответа) Какие из производных вычислены верно? |
ВАРИАНТЫ ОТВЕТОВ: 1.
2.
3.
4.
5.
|
ЗАДАНИЕ № 23. Правило
нахождения производной частного:
|
ВАРИАНТЫ ОТВЕТОВ:
|
ЗАДАНИЕ № 24. Производная
функции
|
ВАРИАНТЫ ОТВЕТОВ: 1.
2.
3.
4.
5. другой ответ |




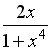 2.
2.