Краткие теоретические сведения

Сущность и формулировки второго закона термодинамики

Первый закон термодинамики позволяет судить о количественных соотношениях в процессах взаимопреобразований тепловой и механической энергий, но не устанавливает условия, при которых эти процессы происходят.

Формулировки условий, необходимых для преобразования одного вида энергии в другой, представляют собой второй закон термодинамики, который, таким образом, является весьма существенным дополнением первого закона. Оба закона термодинамики являются основой современной термодинамики.

Имеется несколько формулировок второго закона термодинамики. Приведем наиболее характерные:

для превращения теплоты в механическую работу необходимо иметь источник теплоты и холодильник с температурой ниже температуры источника, т. е. необходим температурный перепад;

нельзя осуществить тепловой двигатель, единственным результатом действия которого было бы превращение теплоты какого- либо тела в работу без передачи части теплоты другим телам;

теплота не может переходить от менее нагретого тела к более нагретому без совершения внешней работы.

Первые две формулировки относятся к двигателям, в которых теплота превращается в работу, третья формулировка определяет условия работы холодильных установок.

Понятие об энтропии газа и т—s-диаграмма

Рассмотрим произвольный обратимый процесс на — диаграмме, в котором к рабочему телу подводится теплота и осуществляется переход из состояния 1 в состояние 2 (рис.3). Если весь процесс разделить на элементарные отрезки, то для каждого из них количеств подведенной теплоты можно считать бесконечно малой величиной, а температуру рабочего тела постоянной, равной Т. Отношение dq/Т называется приведенной теплотой и обозначается , т. е.

(1.7)

Изменение приведенной теплоты в процессе 1—2

= =

Согласно уравнению первого закона термодинамики, числитель подынтегрального выражения

Рис. 3. к пояснению понятия энтропии газа

Тогда

(1.8)

Из уравнения состояния идеального газа следует, что ,

откуда

.

После интегрирования получим

. (1.9)

Величина называется энтропией. Из уравнения (1.9) видно, что изменение энтропии зависит только от начальных и конечных параметров состояния рабочего тела и, следовательно, энтропия сама является параметром состояния. Уравнение (1.9) определяет связь энтропии с параметрами и , т.е. .

Из уравнения состояния идеального газа, написанного для состояний 1 и 2, имеем

; .

Тогда

Подставив выражения для этих отношений в уравнение (1.9) и используя уравнение Майера, получим еще два уравнения связи энтропии с параметрами состояния рабочего тела, т. е. уравнения вида

и :

; (1.10)

(1.11)

Параметр «энтропия» используют при изучении тепловых процессов и выполнении различных теплотехнических расчетов. По изменению энтропии можно судить о направлении тепловых потоков.

Из уравнения (1.7) следует, что знаки приращения энтропии и теплоты совпадают. Действительно, если ds > 0, то dq> 0, так как температура Т всегда положительна; если же ds < 0, то и dq < 0. Таким образом, если в процессе изменения состояния рабочего тела энтропия уменьшается, то это значит, что теплота отводится от рабочего тела, и, наоборот, если энтропия возрастает, то теплота к рабочему телу подводится.

Для определения количества теплоты, затраченной в каком- либо термодинамическом процессе, производят построение этого процесса на Т—s диаграмме, где по оси ординат отложена температура Т, а по оси абсцисс — энтропия s (рис. 4). Если для процесса 1—2 известна зависимость Т=f(s), то площадь 1—2—3— 4—1 будет равна

Следовательно, на Т— s-диаграмме площадь под кривой процесса изменения состояния рабочего тела численно равна количеству теплоты процесса.

Определим для рассмотренных ранее основных термодинамических процессов.

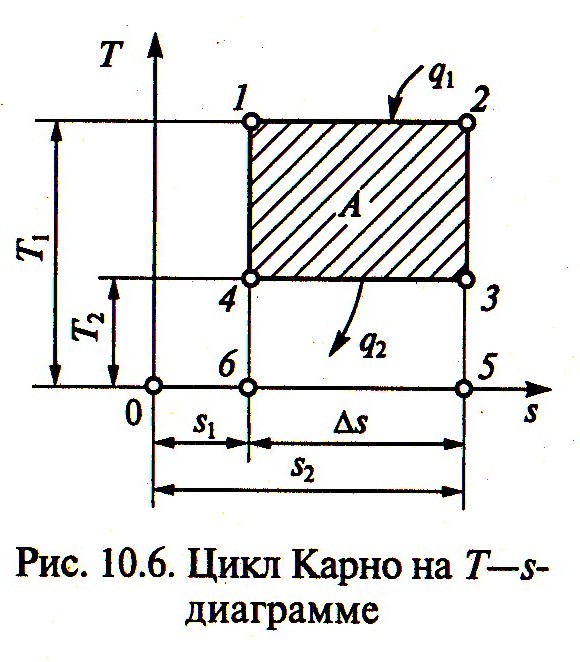
Их графическое изображение на Т—s-диаграмме показано на рис. 5.

Для изохорного процесса ( ) выражение (1.9) принимает вид

(1.12)

В координатах Т—s это логарифмическая кривая, направленная выпуклостью к оси абсцисс. Отрезок кривой отображает нагревание газа, так как, >0, >0. Отрезок соответствует отводу теплоты и охлаждению газа.

Для изобарного процесса ( ) из уравнения (1.10)

Имеем (1.13)

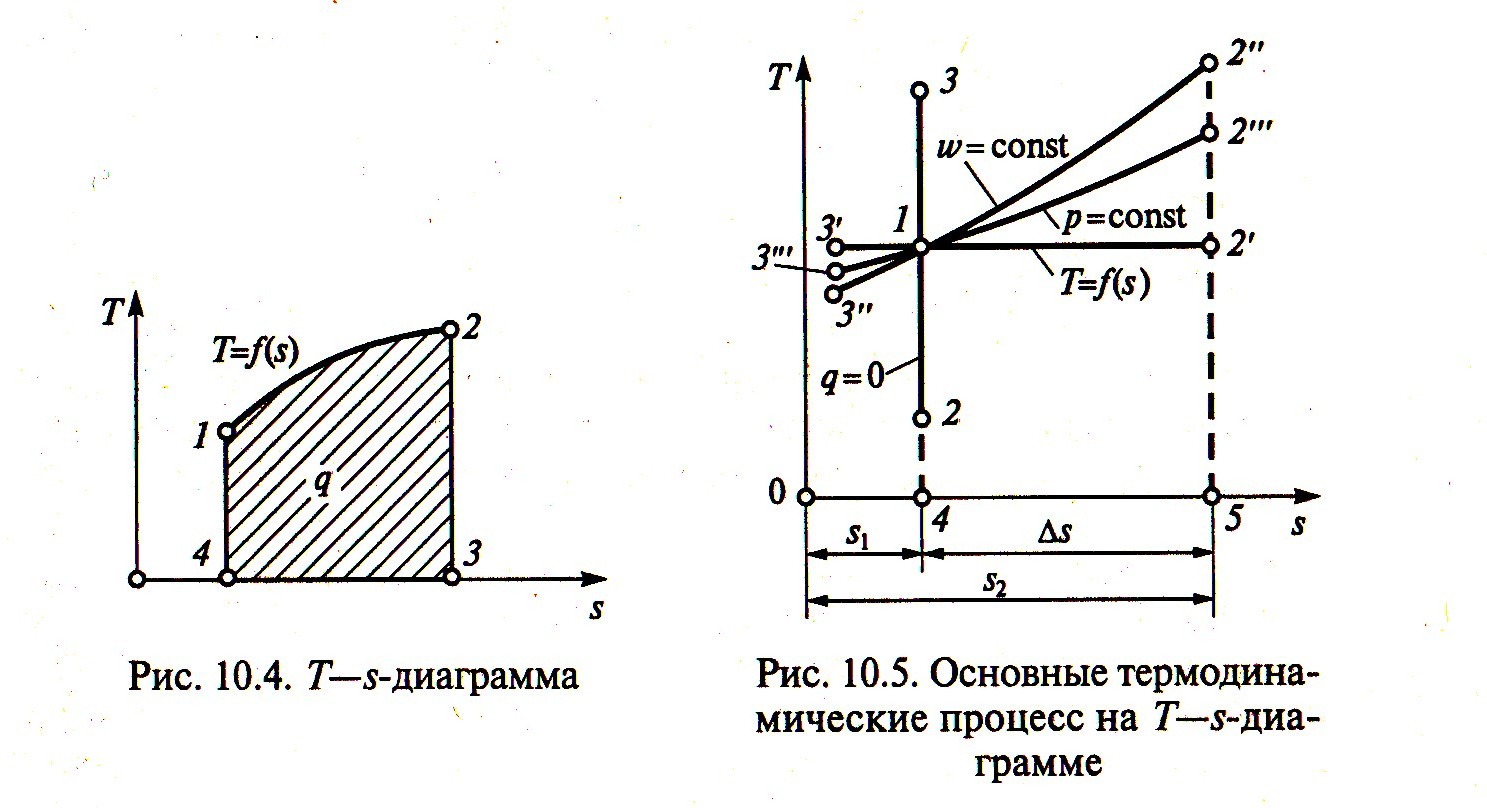
Рис. 4 -диаграмма Рис. 5 Основные термодинамические

процессы на -диаграмме

Рассматривая уравнения (1.12) и (1.13), можно установить, что при одном и том же значении энтропии в изобарном процессе больше, чем в изохорном, так как > . Изобарному процессу на Т — s-диаграмме соответствует кривая .

Изотермический процесс на T s-диаграмме изображается прямой, параллельной оси абсцисс. Отрезок соответствует процессу расширения газа, так как при увеличении энтропии (ds > 0) увеличивается и удельный объем ( > 0). Отрезок ’является изображением процесса изотермического сжатия.

Изменение энтропии газа в изотермическом процессе может быть определено из уравнений (1.9) (1.10):

(1.14)

(1.15)

Количество теплоты - на Т- s диаграмме выражается площадью прямоугольника т.е. .

Тогда

, (1.16)

Как следует из уравнения (10.15), или

(1.17)

Для адиабатного процесса и . Следовательно,

т.е .

Таким образом, адиабатный процесс на Т—s-диаграмме изображается прямой, параллельной оси ординат. Отрезок 1—2 соответствует процессу расширения рабочего тела (T< 0), а 1—З — процессу сжатия.

Циклу Карно на Т—s-диаграмме соответствует прямоугольник (рис 6). Выражение для термического. КПД данного цикла по такой диаграмме получить проще, чем по -диагра мме:

Рис.6 Цикл Карно на Т-s

диаграмме

где , - площади соответствующих прямоугольников.

Пример 1. При совершении обратимого цикла в тепловом двигателе к рабочему телу подводится 440 МДж теплоты. При этом двигатель совершает работу, равную 200 МДж. Определить термический КПД цикла.

Решение. Согласно формуле (1.2)

Пример 2. Определить КПД обратимого цикла теплового двигателя, если подвод теплоты осуществляется при температуре = 200 °С, а отвод — при температуре = 30 °С.

Решение. В соответствии с формулой (1.5)

Пример 3. Определить КПД холодильной машины, работающей по обратному циклу для температурных условий примера 2.

Решение. Согласно формуле (1.6)

Практическая работа № 5.

Тема: Понятие о круговом процессе. Цикл Карно.

Цель работы: ознакомиться с сущностью идеального цикла теплового двигателя и цикла Карно.

Ход работы:

1. Записать определение кругового процесса.

2. Объяснить сущность идеального цикла теплового двигателя.

3. Зарисовать прямой цикл на p-w- диаграмме, записать формулу термического КПД и дать определение прямого цикла.

4. Зарисовать обратный цикл на p-w- диаграмме, записать формулу холодильного коэффициента и дать определение обратного цикла.

5. Объяснить сущность цикла Карно (выполнить рисунок).

6. Записать выводы по термическому коэффициенту цикла Карно.

7. Вывод по работе.

Контрольные вопросы:

1. Каковы отличия реального и идеального циклов?

2. Объясните сущность цикла Карно.

3. Почему в реальных условиях невозможно создать двигатель, работающий по циклу Карно?