Краткие теоретические сведения Понятие о термодинамических процессах

Как было отмечено, в процессе превращения тепловой энергии в механическую участвует рабочее тело, параметры состояния которого изменяются. При термодинамическом исследовании процессов в зависимости от решаемой задачи выделяется определенная группа тел или отдельное тело, которое называется термодинамической системой. Рабочее тело, находящееся в цилиндре и отделенное поршнем от внешней среды, является примером термодинамической системы. Тела, взаимодействующие с системой и влияющие на ее состояние, называют внешней средой.

Систему от внешней среды отделяет контрольная поверхность. Например, для газа, находящегося в цилиндре, контрольной поверхностью являются внутренние поверхности цилиндра и днище поршня.

Для изучения состояния идеального газа условно допускается существование системы, идеально теплоизолированной от внешней среды. Практически такая система не существует, так как абсолютные теплоизоляторы в природе не существуют. Следовательно, любая система взаимодействует с внешней средой.

Термодинамическим процессом называется переход термодинамической системы (рабочего тела) из одного состояния в другое в результате его взаимодействия с внешней средой.

Если изменение состояния внешней среды происходит бесконечно медленно, то и процесс изменения состояния системы, протекающий под воздействием среды, также происходит бесконечно медленно. Можно представить, что в этом случае в каждый момент времени система находится в состоянии равновесия, соответствующем условиям внешней среды.

Равновесным называется такое состояние системы, когда ее параметры во всех точках имеют одинаковые неизменные значения. Процесс, характеризующийся непрерывной последовательностью равновесных состояний системы, называется равновесным процессом. Состояние системы в таком процессе точно определяется параметрами p, w и T. Равновесные процессы являются идеальными.

Реально происходящие в природе процессы не являются равновесными, так как характеризуются конечными значениями скоростей протекания, а также разностями температур и давлений. Однако иногда степень неравновесности столь не значительна, что ею можно пренебречь и с достаточной точностью считать процесс равновесным. Одним из условий равновесности является то, что скорость протекания процесса должна быть мала по сравнению со скоростью звука.

Равновесный процесс, который может быть осуществлен в обратном направлении через тот же ряд равновесных состояний, что и в прямом, как в рабочем теле, так и во внешней среде, называется обратимым процессом.

Изучение обратимых процессов позволяет познать закономерности реальных процессов. Возникающие неточности можно устранить введением соответствующих поправочных коэффициентов.

Внутренняя энергия и работа расширения и сжатия рабочего тела

Внутреннюю энергию рабочего тела составляют кинетическая энергия тепловых движений молекул и колебательных внутримолекулярных движений атомов, а так же потенциальная энергия взаимодействия молекул.

Система в любом состоянии взаимодействия с внешней средой или изолированная обладает определенным количеством внутренней энергии U.

Кинетическая энергия поступательного и вращательного движения молекул, а также энергия колебательного движения атомов зависит только от температуры. Если потенциальную энергию молекул считать равной нулю, т.е. рассматривать идеальный газ, то внутренняя энергия 1 кг такого газа

u = f (T) (1.1)

Изменение внутренней энергии в любом термодинамическом процессе не зависит от характера его протекания, а определяется начальным и конечным состояниями рабочего тела, т.е.

∆u=u₂–u₁ (1.2)

где u₁ и u₂ – внутренняя энергия соответственно в начале и в конце процесса.

Если удельный объем w = const, то работа расширения равно нулю и все количество подведенной теплоты q=c_w(T₂–T₁) расходуется на увеличение внутренней энергии:

u₂ – u₁= c_w(T₂ – T₁) (1.3)

Для бесконечно малого изменения состояния системы du = c_wdT. Внутренняя энергия является параметром состояния.

В общем случае, если к системе подводится теплота, то изменяется не только внутренняя энергия. При расширении рабочего тела им совершается механическая работа. Такая работа считается положительной. При сжатии рабочего тела работа производится со стороны внешней среды. Эта работа считается отрицательной.

Для определения механической работы, совершаемой термодинамической системой, рассмотрим газ, находящийся в цилиндре и давящий на поршень

(рис. 1.) Пусть в какой-то произвольный момент процесса расширения газа его удельный объем изменяется на бесконечно малую величину dw. Давление газа на бесконечно малом участке перемещения поршня ds можно считать постоянным и равным p. Площадь элементарного заштрихованного участка примем равной площади прямоугольника pdw. Площадь под кривой 1-2 можно вычислить путем сложения площадей аналогичных участков, т.е. она равна интегралу pdw от точки 1 до точки 2: ₁

F = ∫₂ pdw. (1.4)

Размерность pdw соответствует размерности работы, производимой 1 кг рабочего тела (Дж/кг).

Элементарная работа, совершаемая при перемещении поршня на бесконечно малую величину ds, м,

dA = pFds, (1.5)

где p - давление в каждый момент времени, Па; F - площадь поршня, м.

Поскольку Fds = dw, то dA = pdw. Следовательно, вся работа расширения на участке 1 – 2

₁

А =∫₂ pdw (1.6)

Сопоставив выражения ( 1.4) и (1.6.), можно констатировать, что площадь под кривой 1-2 соответствует работе, произведенной 1 кг газа в рассматриваемом процессе. Как было сказано ранее, эта работа считается положительной. В процессе 2-1, т.е. при сжатии газа под действием внешней среды (при движении поршня справа налево) работа будет отрицательной. Таким образом, работа в отличие от внутренней энергии зависит от характера протекания процесса и не является параметром состояния.

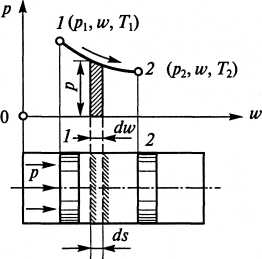
Рис.1 К определению механической работы при расширении рабочего тела