Краткие теоретические сведения Уравнение состояния для реальных газов

Реальный газ в отличие от идеального состоит из молекул, которые имеют конечный объем и взаимодействуют между собой. Поэтому для реальных газов уравнение состояния имеет более сложный вид. При его выводе за основу все же принимают уравнение Клапейрона для идеального газа.

В 1873 г. голландский физик Ван-дер-Ваальс теоретическим путем получил уравнение состояния для идеальных газов, имеющее достаточно простой вид:

, (1.1)

где a и b – поправочные коэффициенты к уравнению Клапейрона, учитывающие физическую природу газа.

Поправочное значение а/ω² характеризует силы взаимного притяжения молекул реального газа и имеет размерность давления. Поправочный коэффициент b представляет собой предельный объем, который имел бы газ при бесконечно большом сжатии, т.е. является, таким образом, собственным объемом молекул реального газа. Измеряется коэффициент b в единицах объема. Поправочные коэффициенты a и b различны для разных газов, что несколько осложняет практические расчеты.

М.П. Вукалович и И.И. Новиков в 1939 г. предложили уравнение состояния для водяного пара с поправкой на ассоциацию и диссоциацию молекул. Ассоциация – это механическое соединение двух или более молекул в одну сложную частицу, происходящее при низких температурах, а диссоциация – обратное явление, происходящее при высоких температурах газа. При учете эффекта ассоциации двойных молекул уравнение Вукаловича – Новикова выглядит следующим образом:

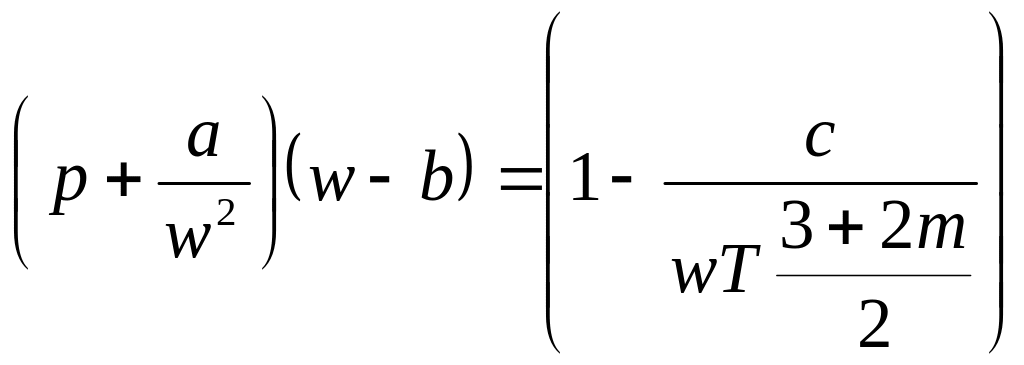, (1.2)

где c и m – опытные постоянные коэффициенты.

Из анализа уравнений (1.1) и (1.2) следует, что состояние реального газа будет тем ближе к состоянию идеального, чем больше ω. Таким образом, при больших удельных объемах реального газа можно пользоваться уравнением Клапейрона. В частности, оно применимо для пара, находящегося во влажном воздухе.

Рассмотрение процесса парообразования

По p-w-диаграмме

Пусть в цилиндре под поршнем находится 1 кг воды при температуре С. При некотором давлении p=const этому состоянию воды соответствует точка а на p – w –диаграмме (рис. 1.1). Удельный объем воды

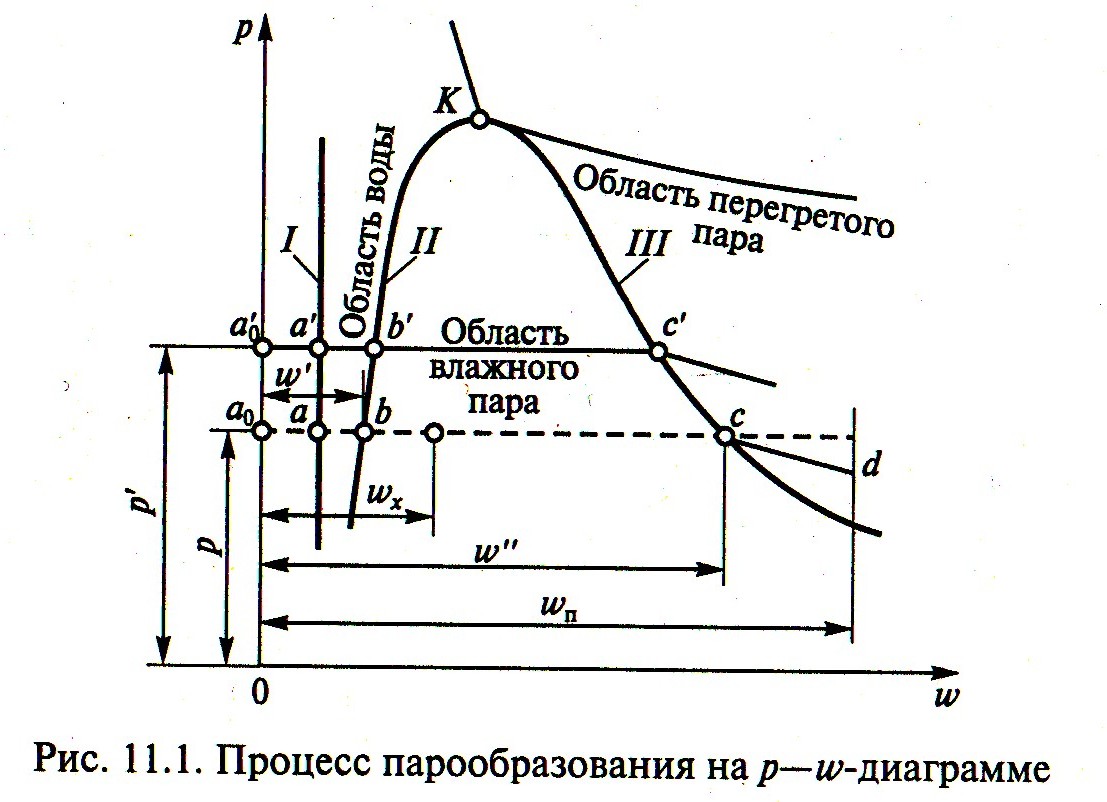
Рис.1 Процесс парообразования на р-w - диаграмме

Если нагревать воду при постоянном давлении до температуры кипения, то ее объем будет увеличиваться и достигнет значения ω′, которому соответствует точка b на p – ω-диаграмме. Следует отметить, что отношение объемов воды и пара на диаграмме искажено. Это обусловлено тем, что при невысоких давлениях объем воды пренебрежимо мал по сравнению с объемом насыщенного пара и отобразить это соотношение на диаграмме, построенной в обычных координатах, не представляется возможным. Это замечание относится также к увеличению объема воды при нагревании ее от 0°С до температуры кипения.

Отрезок прямой b – c на p – ω- диаграмме соответствует процессу парообразования в случае подвода теплоты при неизменных давлении и температуре пароводяной смеси. На отрезке b – c пар называется влажным насыщенным. Когда вся вода превратится в пар (точка с), объем цилиндра окажется заполненным сухим насыщенным паром. Температура пара в точке с, равная температуре кипения, называется температурой насыщения. Она обозначается t_н и зависит от давления. Например, при p_абс = 0,1 МПа t_н = 99, 09°С; при p_абс = 0,2 МПа t_н = 119,62°С; при p_абс = 10 МПа t_н = 309,53°С.

Процесс, обратный процессу парообразования, т.е. протекающий от точки с до точки b, является процессом отвода теплоты при постоянных давлении и температуре, в результате которого 1 кг сухого пара, постепенно конденсируясь, превращается в 1 кг воды. Другими словами, это процесс конденсации.

Влажный пар характеризуется степенью сухости x, т.е. массовой долей сухого насыщенного пара, содержащегося в 1 кг влажного пара. Например, если в 1 кг влажного пара содержится 0,75 кг сухого пара и 0,25 кг воды, то степень сухости такого пара х = 0,75.

Величина (1 – х), соответствующая доле воды во влажном паре, называется степенью влажности. Для сухого насыщенного пара х = 1.

Если процесс парообразования будет осуществляться при более высоком давлении p′, то удельный объем воды практически не изменится (точка а′), а удельный объем кипящей воды несколько возрастет (точка b′), так как с увеличением давления возрастет температура кипения. Состоянию сухого насыщенного пара соответствует точка с′, в которой его удельный объем меньше, чем при давлении p (точка с), так как процесс парообразования при более высоком давлении происходит более интенсивно.

Если соответствующие точки (а, а′, …; b, b′, …; с, с′, …) соединить, то образуются линии, характеризующие различные состояния воды и водяного пара. Так, как линия I соответствует состоянию воды при 0°С и является прямой, почти параллельной оси ординат. Линия II, объединяющая точки b, b′, …, - кривая, которая соответствует состоянию кипящей воды и называется нижней пограничной кривой. Линия III, объединяющая точки с, с′, …, - кривая, которая характеризует состояние сухого насыщенного пара при различных давлениях и называется верхней пограничной кривой. Линия II отделяет область воды от области влажного пара, а линия III – область влажного пара от области перегретого пара.

Линии II и III встречаются в точке K, которая называется критической. Она соответствует критическому состоянию вещества, при котором отсутствует различие между жидкостью и паром. В этой точке кипящая жидкость мгновенно переходит в сухой пар, так как горизонтальный отрезок прямой между линиями II и III, характеризующий процесс парообразования, отсутствует. Параметры, определяющие точку K, называются критическими; для воды они имеют следующие значения: p_кр = 22,5 МПа; t_кр = 374,15°С

(Т_кр = 647,3 К), ω_кр = 0,00307 м³/кг.

Как было отмечено ранее, процесс парообразования, изображаемый отрезком b – c, требует подвода теплоты. Количество теплоты, необходимое для превращения 1 кг воды в сухой насыщенный пар, называется теплотой парообразования и обозначается буквой r. С увеличением давления значение r уменьшается; при p_абс= 10 МПа r = 1330 кДж/кг; в точке K r = 0.

Если к сухому насыщенному пару продолжать подводить теплоту при

p = const, то пойдет процесс, которому на p – ω-диаграмме соответствует линия c – d. Она уже не совпадает с изотермой, так как подведенная теплота расходуется на повышение температуры пара. Пар в состоянии, характеризуемом линией процесса за точкой с, например в точке d, имеет температуру более высокую, чем температура насыщения, и называется перегретым паром.

Для параметров, характеризующих состояние воды или пара, приняты следующие обозначения: величины с индексом 0 относятся к начальному состоянию воды; с индексом ′ - к воде при температуре кипения; с индексом ′′ - к сухому насыщенному пару; с индексом x – к влажному насыщенному пару; с индексом п – к перегретому пару.

Если известна степень сухости влажного насыщенного пара, то представляется возможным определить его остальные параметры состояния. Пусть доля сухого пара в пароводяной смеси составляет x. Тогда (1 – x) – доля воды. Объем 1 кг смеси

ωx = ω"x + ω′ (1 – x). (1.3)

Значения удельных объемов воды ω′ и сухого насыщенного пара ω" приводятся в справочных таблицах. При большом паросодержании (x>0,8) и невысоком давлении (p_абс<3 МПа) второй член выражения (1.3) пренебрежимо мал по сравнению с первым. Тогда

ωx = ω"x. (1.4)

Выражение (1.3) можно также представить в виде

ωx = ω′ + x(ω" - ω′). (1.5)

Плотность влажного насыщенного пара

(1.6)

т.е. она равна отношения плотности сухого насыщенного пара к степени сухости.

Теплота парообразования (фазового превращения)

r_х = rx. (1.7)

Энтальпия влажного насыщенного пара

i_х = i′ + x(i" - i′) = i′ + rx. (1.8)

Энтропия влажного насыщенного пара

(1.9)

где s′ - удельная энтропия воды при температуре кипения;

xr/Т_н – приращение удельной энтропии при испарении x кг воды; Т_н – температура насыщенного пара.

Энтальпия перегретого пара

i_п = i" + q_п, (1.10)

т.е. она представляет собой сумму энтальпии сухого насыщенного пара и теплоты, израсходованной на перегрев пара при p = const.

Практическая работа № 8.

Тема: Теплопроводность. Конвективный теплообмен.

Цель работы: ознакомиться с видами теплообмена, основными понятиями и определениями и законом Фурь; с формулами определения теплового потока при конвективном теплообмене и факторами, влияющими на коэффициент теплоотдачи.

Ход работы:

1. Объяснить механизм обмена энергией в процессе теплопроводности.

2. Что такое тепловое излучение?

3. Дайте определение конвективного теплообмена. Назовите виды конвекции. Объясните их механизм действия.

4. Какой тепловой процесс называется теплопередачей?

5. Дайте определение теплового потока.

6. Какое температурное поле называют стационарным?

7. Сформулируйте понятие температурного градиента.

8. Напишите математическое выражение закона теплопроводности Фурье.

9. От каких переменных зависит коэффициент теплопроводности?

10. Запишите формулу, выражающую зависимость удельного теплового потока от термического сопротивления стенки.

11. Напишите формулу Ньютона для определения теплового потока при конвективном теплообмене.

12. Запишите основные критерии подобия, используемые при определении коэффициента теплоотдачи.

13. Вывод по работе.

Контрольные вопросы:

1. Назовите три основных вида теплообмена.

2. Объяснить механизм обмена энергией в процессе теплопроводности.

3. Дайте определение конвективного теплообмена. Назовите виды конвекции. Объясните их механизм действия. Перечислите факторы, от которых зависит теплоотдача конвекцией.

4. Что такое тепловое излучение?

5. Какой тепловой процесс называется теплопередачей?

6. Напишите формулу Ньютона для определения теплового потока при конвективном теплообмене.