
- •Распределение максвелла и больцмана
- •I начало термодинамики
- •Уравнение равновесного состояния идеального газа
- •Средняя энергия молекул
- •Выводы из таблицы, примеры и дополнение
- •II начало термодинамики. Энтропия
- •Замкнутая (изолированная) система
- •Незамкнутая (неизолированная) система
- •Список основных формул
- •II начало термодинамики. Энтропия. Циклы
- •I начало термодинамики. Работа при изопроцессах
- •Средняя энергия молекул
Распределение максвелла и больцмана
Распределение Больцмана (распределение частиц в силовом поле, в однородном поле силы тяжести)
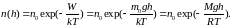
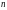 – концентрация
частиц,
– концентрация
частиц,
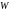 –
их потенциальная энергия (
–
их потенциальная энергия (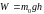 ),
),
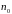 –
концентрация частиц в точках поля, где
–
концентрация частиц в точках поля, где
 (
( ),
),
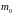 –
масса частицы,
–
масса частицы,
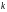 –
постоянная Больцмана,
–
постоянная Больцмана,
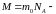 молярная
масса,
молярная
масса,
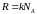 –
газовая постоянная.
–
газовая постоянная.
Барометрическая формула (распределение давления в силовом поле, в однородном поле силы тяжести)
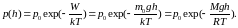
Распределение Максвелла (молекул по скоростям в газе, находящемся в равновесном состоянии)
Вероятность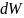 того, что
скорость молекулы, заключена в интервале
от
того, что
скорость молекулы, заключена в интервале
от
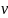 до
до
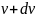 или доля
молекул
или доля
молекул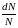 ,
скорость которых заключена в интервале
от
до
,
скорость которых заключена в интервале
от
до
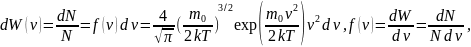
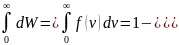 площадь под
кривой
площадь под
кривой
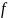 от
от
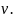
Здесь
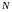 –
полное число молекул,
–
полное число молекул,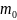 –
масса молекулы,
–
масса молекулы,
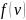 –
вероятность того, что скорость молекулы,
заключена в интервале от
до
в расчете на единицу интервала скорости
(
–
вероятность того, что скорость молекулы,
заключена в интервале от
до
в расчете на единицу интервала скорости
(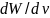 ),
или доля молекул, скорости которых
заключены в интервале от
до
в
расчете на единицу интервала скорости
),
или доля молекул, скорости которых
заключены в интервале от
до
в
расчете на единицу интервала скорости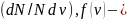 функция распределения молекул по
скоростям (плотность вероятности).
функция распределения молекул по
скоростям (плотность вероятности).
Число молекул
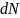 ,
скорость
которых заключена в интервале от
до
,
скорость
которых заключена в интервале от
до
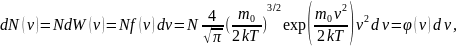
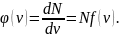
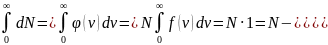 площадь
под кривой
площадь
под кривой
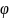 от
от
Здесь
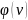 –
число молекул, скорости которых заключены
в интервале от
до
в расчете на единицу интервала скорости
–
число молекул, скорости которых заключены
в интервале от
до
в расчете на единицу интервала скорости
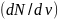 .
.
Свойства функции плотности вероятности .
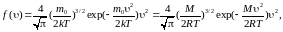
υВЕР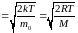 ,
,
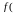 υВЕР
υВЕР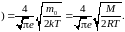
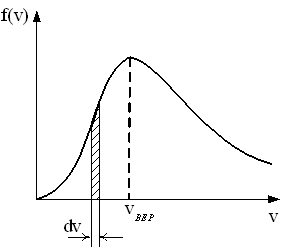
υВЕР )
υВЕР
При
росте
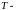 максимум
сместится
вправо (значение
υВЕР
увеличится),
а его
высота (значение
υВЕР
)) уменьшится
и наоборот.
максимум
сместится
вправо (значение
υВЕР
увеличится),
а его
высота (значение
υВЕР
)) уменьшится
и наоборот.
При
росте
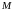 или
или
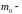 максимум
сместится
влево (значение
υВЕР
уменьшится),
а его
высота (значение
υВЕР
)) увеличится
и наоборот.
максимум
сместится
влево (значение
υВЕР
уменьшится),
а его
высота (значение
υВЕР
)) увеличится
и наоборот.
I начало термодинамики
(закон сохранения энергии для тепловых явлений)
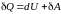 ,
,
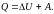
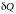 и
и
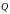 –
бесконечно
малое и конечное количество тепла,
подводимое
к системе.
–
бесконечно
малое и конечное количество тепла,
подводимое
к системе.
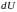 и
и
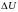 –
бесконечно
малое и конечное приращение
внутренней
энергии системы.
–
бесконечно
малое и конечное приращение
внутренней
энергии системы.
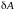 и
и
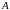 –
бесконечно малая и
конечная работа, совершаемая системой
против
внешних сил,
т.
е. над внешними телами. Все переменные
могут быть как положительными, так
отрицательными и нулевыми.
–
бесконечно малая и
конечная работа, совершаемая системой
против
внешних сил,
т.
е. над внешними телами. Все переменные
могут быть как положительными, так
отрицательными и нулевыми.
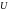 –
внутренняя
энергия системы
[Дж]: сумма
кинетической энергии хаотического
движения молекул, потенциальной энергии
взаимодействия между молекулами и
внутримолекулярной энергии. Система,
находящаяся в одном
и том же состоянии (набор
–
внутренняя
энергия системы
[Дж]: сумма
кинетической энергии хаотического
движения молекул, потенциальной энергии
взаимодействия между молекулами и
внутримолекулярной энергии. Система,
находящаяся в одном
и том же состоянии (набор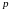 ,
,
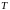 ,
,
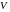 для
идеального газа),
имеет одну и ту же
внутреннюю
энергию
,
т. е.
– функция состояния системы.
– тепло
[Дж],
–
работа [Дж].
для
идеального газа),
имеет одну и ту же
внутреннюю
энергию
,
т. е.
– функция состояния системы.
– тепло
[Дж],
–
работа [Дж].
Моль
–
количество
вещества, в котором содержится
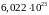 частиц.
частиц.
Идеальный газ – система не взаимодействующих друг с другом частиц.
Параметры состояния системы – давление , температура , объем и т. д.
Равновесное состояние – все параметры системы имеют определенные значения, не меняющиеся при неизменных внешних условиях.
Равновесный (квазиравновесный) процесс – бесконечно медленный процесс, состоящий из последовательности равновесных состояний. Такой процесс – обратимый. Неравновесный процесс – необратимый.
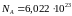 моль-1
– число Авогадро,
–
постоянная
Больцмана
[Дж/K],
–
газовая постоянная
[Дж/К
моль-1
– число Авогадро,
–
постоянная
Больцмана
[Дж/K],
–
газовая постоянная
[Дж/К моль],
–
масса молекулы [кг],
–
число частиц вещества,
моль],
–
масса молекулы [кг],
–
число частиц вещества,
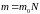 –
масса вещества [кг],
–
масса вещества [кг],
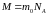 –
молярная
масса
[кг∙моль-1],
–
молярная
масса
[кг∙моль-1],
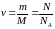 –
число молей
вещества [моль].
–
число молей
вещества [моль].
