
- •Функция шегінің Гейне және Коши бойынша анықтамасы. Мысал.
- •Б). Екінші тамаша шек.
- •Мысалдар:
- •5. Монотонды тізбектердің анықтамасы:
- •6. Мен нақты сандар жиыны болсын. Әрбір санына жиынының санын сәйкес қоятын ережесі жиынында берілген санды функция деп аталады және ол
- •10. Анықтама. Санынан айырымының абсолют шамасы -нан кіші сандардан құрылған жиынын нүктесінің - маңайы деп атайды, және
- •11. Функциясы нүктесінде және оның белгілі бір маңайында анықталған, сонымен бірге мен шектері бар және
- •14. Функциясы нүктесінде және оның қандайда бір маңайында анықталған функция болсын. - нүктесіндегі аргумент өсімшесі , ал оған сәйкес келетін функция өсімшесі:
- •1) ; 2) Шарттарының орындалуы қажетті және жеткілікті. Онда
- •Туындының механикалық және геометриялық мағынасы
Функцияның өсуі және кемуі. Мысал.
Теорема – 1:
Егер
дифференциалданатын f(x)
функциясы (a,b)
аралығында өспелі (кемімелі) болса, онда
![]() үшін
үшін
![]()
![]() .
.
Дәлелдеу:
f(x)
функциясы (a,b)
аралығында өспелі болсын. Және (a,b)
аралығына тиісті кез-келген x
және x+∆x
алайық . Сосын ![]() қатынасын
қарастырайық. f(x)
функциясы
өспелі сол
қатынасын
қарастырайық. f(x)
функциясы
өспелі сол
с![]() ебепті
ебепті
![]() онда
онда
![]() және
және
![]() егер
егер
![]() және
және
.![]() .Екі жағдайда да
, алымы мен
бөлімінің таңбасы
.Екі жағдайда да
, алымы мен
бөлімінің таңбасы
б![]() ірдей
болғандықтан теорема бойынша f(x)
функциясы
x
нүктесінде туындысы бар және алдыңғы
қатынастың шегі болады. Содан
шығады.
ірдей
болғандықтан теорема бойынша f(x)
функциясы
x
нүктесінде туындысы бар және алдыңғы
қатынастың шегі болады. Содан
шығады.
Теорема – 2:
Е![]()
![]() гер
f(x)
функциясы
(a,b)
интервалында дифференциалданатын болса
және үшін
гер
f(x)
функциясы
(a,b)
интервалында дифференциалданатын болса
және үшін
орындалатын болса, онда осы функция (a,b) интервалында өспелі (кемімелі) болады.
Мысал:
 функциясын
өсу мен кемуге зерттеу.
функциясын
өсу мен кемуге зерттеу.
Ф![]() ункция
барлық сандар тізбегінде анықталған:
ункция
барлық сандар тізбегінде анықталған:
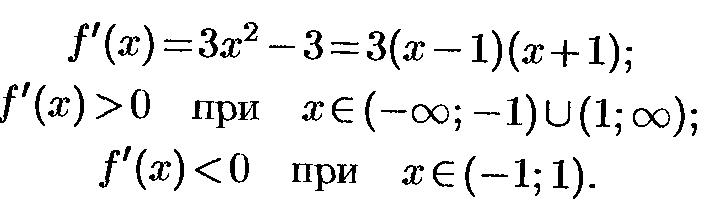
Ақырсыз аз функцияның негізгі қасиеттері.\
А.А.Ф.-дың алгералық қосындысы да А.А.Ф. болады.
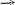 x
x![]()
![]() x0-ге
ұмтылғанда α(x)
және β(x)
функциялары ақырсыз аз болсын. Одан
кез-келген 𝜀>0
үшін
x0-ге
ұмтылғанда α(x)
және β(x)
функциялары ақырсыз аз болсын. Одан
кез-келген 𝜀>0
үшін
 орындалады, онда ε/2>0
болады.
Осыдан
орындалады, онда ε/2>0
болады.
Осыдан
 оындалатын
оындалатын
 саны
табылып, мына теңдік орындалады.
(1) және
саны
табылып, мына теңдік орындалады.
(1) және ![]() онда
(2)
онда
(2)
δ
– δ1
және δ2
кіші
сан болсын. Сонда ![]() теңсіздігін қанағаттандыратын
барлық х үшін (1)және (2) теңсіздік
орындалады. Содан мына қатынас пайда
болады.
теңсіздігін қанағаттандыратын
барлық х үшін (1)және (2) теңсіздік
орындалады. Содан мына қатынас пайда
болады.
![]()
![]()
Содан,
Ол дегеніміз
 үшін
үшін ![]() ввввввввввввввввввввввввввввввввв
-—ақырсыз аз.
ввввввввввввввввввввввввввввввввв
-—ақырсыз аз.
Ақырсыз аз функцияның көбейтіндісі де А.А.Ф. болады.
![]() де
f(x) функциясы шектелген болсын. Сонда
M>0 саны табылсын, және x0
нүктесінің δ1
маңайындағы барлық х үшін мына теңсіздік
орындалады.
де
f(x) функциясы шектелген болсын. Сонда
M>0 саны табылсын, және x0
нүктесінің δ1
маңайындағы барлық х үшін мына теңсіздік
орындалады.
(1)
және
де
α![]() (x)
функциясы ақырсыз аз болсын. Сонда
кез-келген ε>0
үшін, және ε/M>0
үшін δ2>0
саны табылады және мына теңсіздік
орындалады.
(x)
функциясы ақырсыз аз болсын. Сонда
кез-келген ε>0
үшін, және ε/M>0
үшін δ2>0
саны табылады және мына теңсіздік
орындалады.
(2)
δ![]() арқылы δ1
және δ2
кіші
сандарды белгілейміз. Сонда
теңсіздігін қанағаттандыратын барлық
х үшін (1) және(2) теңсіздіктер орындалады.
Содан
арқылы δ1
және δ2
кіші
сандарды белгілейміз. Сонда
теңсіздігін қанағаттандыратын барлық
х үшін (1) және(2) теңсіздіктер орындалады.
Содан
 Ол дегеніміз
үшін
Ол дегеніміз
үшін
 – ақырсыз аз функция.
– ақырсыз аз функция.
Функция шегінің Гейне және Коши бойынша анықтамасы. Мысал.
(Гейне)
A саны y=f(x) функциясының x→x0 ұмтылғандағы шегі деп аталады, егер x0 санына ұмтылған кез келген x1, x2, x3,… сандар тізбегі үшін сәйкесінше f(x1), f(x2), f(x3),… сандар тізбегі A санына ұмтылса.
Б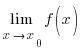 ұны
=
A деп белгілейді.
ұны
=
A деп белгілейді.
(Коши)
А саны функция шегі деп
аталады. Егер алдын-ала берілген ε
оң санына δ оң саны табылып, х-тің х0-ге
тең емес
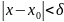 қанағаттандыратын мәндері үшін,
қанағаттандыратын мәндері үшін,
 орындалуы керек.
орындалуы керек.
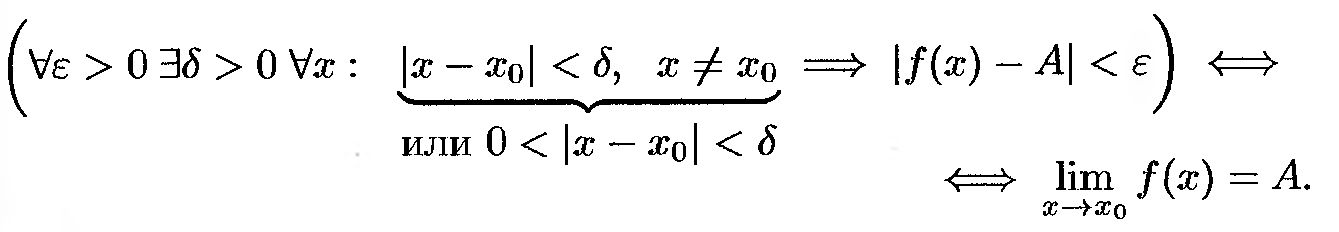
Мысал.
![]()
y = x2 болса онда .
Өйткені нөлге ұмтылған кез келген x1, x2, x3,… сандар тізбегі үшінx12, x22, x32,… сандар тізбегі де нөлге ұмтылады
Бірінші және екінші тамаша шектер.
Тамаша шектер.
А). Бірінші тамаша шек.
Теорема

Дәлелі: 0А=1 сызбадан десек АВ=sinx 0В=cosx және CD=tgx болады.

Сонымен
бірге
 (1)
(1)
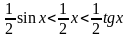 (2)
(2)
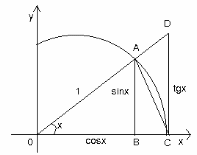
(2)ні
 ке
көбейтсек онда
ке
көбейтсек онда
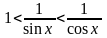 болады немесе
болады немесе
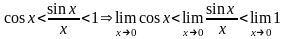
Шегі
бар функциялардың 4-ші қасиетінен
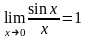 келісіп шығарады.
келісіп шығарады.
Мысалдар:
1)

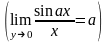
2)
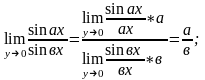
3)
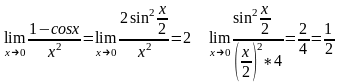
Б). Екінші тамаша шек.
Теорема:
 сан тізбегінің шегі
сан тізбегінің шегі
 да 2 мен 3 арасындағы санға ұмтылады.
да 2 мен 3 арасындағы санға ұмтылады.
Дәлелі:
ді
Ньютон биномы
 бойынша жіктейік. Бұл жерде x=1
бойынша жіктейік. Бұл жерде x=1
 болғандығы үшін
болғандығы үшін


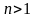 болғанда
(1)-дің барлық мүшелері оң таңбалы және
олар
болғанда
(1)-дің барлық мүшелері оң таңбалы және
олар
 (2) сан тізбегі сәйкес мүшелерінен
үлкен емес, ал (2) нің жақша ішіндегі
бөлігі
(2) сан тізбегі сәйкес мүшелерінен
үлкен емес, ал (2) нің жақша ішіндегі
бөлігі
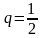 болған кемейуіші геометриялық прогрессия
болған кемейуіші геометриялық прогрессия
 .
Сондықтан
.
Сондықтан
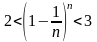 теңсіздігі орындалады. Яғни
теңсіздігі орындалады. Яғни
 ті аламыз.
ті аламыз.
Анықтама:
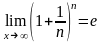 е иррационал сан болып ол 2,7182818284... ке
тең.
е иррационал сан болып ол 2,7182818284... ке
тең.
Теорема:
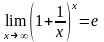
Дәлелі.
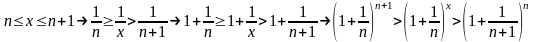

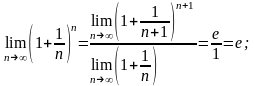
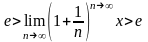 ден
ден
 келіп шығады.
келіп шығады.
Мысалдар:
1)
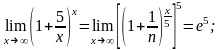
2)
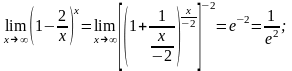
10. Жиындардың теңдігі. Жоғарыда анықталған
 кірістіру символы бойынша жиындардың
теңдігі анықталады.
кірістіру символы бойынша жиындардың
теңдігі анықталады.
Егер
 және
және
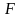 жиындары үшін
жиындары үшін
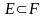 және
және
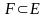 кірістірулері бірдей орындалса, онда
және
кірістірулері бірдей орындалса, онда
және
 жиындары тең дейді де ,
жиындары тең дейді де ,
 символымен белгілейді.
символымен белгілейді.
20.
Жиындардың қиылысуы.
және
жиындарының қиылысуы
деп
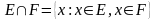 жиынын, яғни
және
жиындарында бірдей жататын
жиынын, яғни
және
жиындарында бірдей жататын
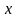 элементтерінен құрылған жиын аталады.
элементтерінен құрылған жиын аталады.
30.
Жиындардың біріктіруі.
және
жиындардың біріктіруі деп
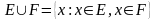 жиынын, яғни
және
жиындарының кемінде біреуінде жатқан
элементтеріне құрылған жиынды айтады
( бұған
мен
-те
жататын элементтер де кіреді ).
жиынын, яғни
және
жиындарының кемінде біреуінде жатқан
элементтеріне құрылған жиынды айтады
( бұған
мен
-те
жататын элементтер де кіреді ).
40.
Жиындардың айырымы.
және
жиындарының айырымы
деп
 жиыны, яғни
жиынында жатып,
жиынында жатпайтын
элементтерінің жиыны ататлады.
жиыны, яғни
жиынында жатып,
жиынында жатпайтын
элементтерінің жиыны ататлады.
2.
1- анықтама. Егер
![]() санға белгілі бір ереже (заң) бойынша
санға белгілі бір ереже (заң) бойынша
![]() нақты саны сәйкестендірілсе, онда сан
тізбегі немесе жай тізбек берілген
дейді.
нақты саны сәйкестендірілсе, онда сан
тізбегі немесе жай тізбек берілген
дейді.
Тізбекті
![]()
![]()
![]()
![]()
символдарының біреуімен белгілейді.
2-
анықтама. Егер кез келген
![]() санына сәйкес N=N(
санына сәйкес N=N(![]() )
саны табылып,
)
саны табылып,
![]() үшін
үшін
![]()
теңсіздігі
орындалса, а санын
![]() тізбегінің шегі деп атайды да оны былай
жазады:
тізбегінің шегі деп атайды да оны былай
жазады:
![]()
Анықтама. Егер lim (x) 0 болса, онда 0 õõ жағдайда (x) шексіз аз
x x 0 функция деп аталады.
Шексіз аз функциялардың негізгі қасиеттері:
0 1 . Бірнеше шексіз аз функциялардың қосындысы мен кӛбейтінділері
( 0 õõ ) – да шексіз аз функция болады.
0 2 . Шексіз аз функция мен шектелген функцияның кӛбейтіндісі 0 õõ -
да шексіз аз функция болады.
Анықтама. Егер кез келген ε>0 саны үшін () саны табылып,
0x x 0 шартын қанағаттандыратын барлық х үшін f (x) теңсіздігі
орындалса, онда f(x) функциясын 0 õõ жағдайда шексіз үлкен функция деп
атайды және былай белгілейді lim f (x)
õ õ0
Шексіз үлкен функциялардың негізгі қасиеттері:
0 1 . Бірнеше шексіз үлкен функциялардың қосындысы мен кӛбейтінділері
шексіз үлкен функция болады.
0 2 . Шектелген f xC1 0 функция мен шексіз үлкен функциялардың
0 õõ - дағы кӛбейтіндісі - f f 1 - шексіз үлкен функция болады.
3.
3- анықтама. Егер тізбек шегі
![]() саны тиянақты (шекті) сан болса, онда
оны а санына жинақты дейді.
4-
анықтама. Егер тізбектің шегі жоқ немесе
саны тиянақты (шекті) сан болса, онда
оны а санына жинақты дейді.
4-
анықтама. Егер тізбектің шегі жоқ немесе
![]() болса, онда ол тізбекті жинақсыз дейді.
болса, онда ол тізбекті жинақсыз дейді.
1-теорема. Жинақты тізбектің тек бір ғана шегі бар.
2-теорема. Кез келген жинақты тізбек шектелген.
Ескерту. Кез келген шектелген тізбек жинақты деуге болмайды.
3
–теорема. Егер {xn},
{yn}
тізбектері жинақты және
,
![]() болса, онда
болса, онда
{xn
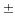 yn}
тізбегі жинақты,
lim(xn
yn)
= a
b.
yn}
тізбегі жинақты,
lim(xn
yn)
= a
b.
n![]()
{xn
 yn}
тізбегі
жинақты,
lim(xn
yn)
=
a
b.
yn}
тізбегі
жинақты,
lim(xn
yn)
=
a
b.
n
{
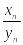 },
b
},
b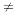 0
тізбегі
жинақты,
lim
=
0
тізбегі
жинақты,
lim
=
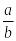
n
4
–теорема. {xn},
{yn},
{zn}
үш тізбек үшін xn
![]() zn
yn
теңсіздігі
орындалса және
zn
yn
теңсіздігі
орындалса және
lim xn= a, lim yn= b болса, онда lim zn= a
n n n
4.
4-
анықтама. Егер
![]() саны үшін N номері табылып
саны үшін N номері табылып
![]() шартын қанағаттандыратын барлық n, m
номері үшін
шартын қанағаттандыратын барлық n, m
номері үшін
![]()
теңсіздігі орындалса, онда тізбегін Коши шартын қанағаттандырады немесе фундаментальды тізбек деп атайды.
Теорема (Коши критериі). Тізбек жинақты болу үшін оның фундаментальды болуы қажетті және жеткілікті.
Егер
кез келген
 саны арқылы барлық
саны арқылы барлық
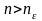 нөмірлері үшін
нөмірлері үшін
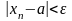 теңсіздігі орындалатындай
теңсіздігі орындалатындай
 оң саны (
оң саны (
санына тәуелді) табылса
онда а саны
санына тәуелді) табылса
онда а саны
 тізбегінің шегі
деп аталады да
тізбегінің шегі
деп аталады да
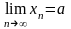 немесе
немесе
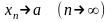
арқылы
белгіленеді
және
тізбегінің
 санына тең шегі бар,
немесе
тізбегі а
санына ұмтылады немесе
тізбегі
а санына жинақталады
дейді.
санына тең шегі бар,
немесе
тізбегі а
санына ұмтылады немесе
тізбегі
а санына жинақталады
дейді.
