1.24 Расчет ременных передач по тяговой способности
Согласно кривым скольжения (см. рис. Р.12) прочность ремня не является достаточным условием, определяющим работоспособность передачи, так как ремень, рассчитанный на прочность, может оказаться недогруженным или же будет буксовать. Основным расчетом ременных передач является расчет по тяговой способности, основанный на кривых скольжения. Этот расчет одновременно обеспечивает требуемую прочность ремней.
Расчет по тяговой способности сводится к определению расчетной площади сечения ремня:
F=P/[kП], (Р.22)
где Р - передаваемое окружное усилие
[kП] - допускаемое полезное напряжение в ремне, полученное согласно кривым скольжения [формула (Р.19)].
Для плоскоременной передачи F=δb где δ и b - толщина и ширина ремня.
Для клиноременной передачи F=zF0 где F0 - площадь поперечного сечения одного ремня (см. табл. 9.2); z - число ремней. Рекомендуется z<=8, так как при большем числе клиновых ремней нельзя гарантировать равномерность их нагружения.
1.25. Расчет ременных передач на долговечность
Долговечность ремня определяется в основном его усталостной прочностью, которая зависит не только от величины напряжений, но также и от частоты циклов напряжений, т. е. от числа изгибов ремня в единицу времени. Для уменьшения напряжений изгиба [формула (Р.14)] рекомендуется выбирать возможно меньшее отношение δ/D1, что благоприятно влияет на долговечность, а также и на тяговую способность передачи (см. табл. 9.3). Полный цикл напряжений (см. рис. Р.10) соответствует одному пробегу ремня.
Полное число пробегов ремня за весь срок работы передачи пропорционально числу пробегов в секунду:
и=v/L<=[и] (Р.23)
где v - скорость ремня в м/сек;
L - длина ремня в м;
[и] - допускаемое число пробегов в секунду.
Число пробегов является скоростным фактором, влияющим на долговечность: чем больше и, тем выше частота циклов, тем меньше срок службы ремня. В связи с тем что пока еще нет метода расчета ремней на долговечность, учитывающего все влияющие на нее факторы, то расчет ремней на долговечность ограничивают выбором δ/D1 в рекомендуемых пределах и проверкой числа пробегов ремня в секунду.
Практика рекомендует: для плоскоременной передачи [и]<=5 1/сек, для клиноременной - [и] <= 10 1/сек.
Ремни, рассчитанные по тяговой способности, обладают нормальной долговечностью, которая в среднескоростных передачах равна 2000 - 5000 ч.
1.26. Последовательность расчета плоскоременных передач
(см. решение примера 36)
Исходные данные:
1. Мощность на валу малого шкива N1.
2. Угловые скорости шкивов ω1 и ω2.
3. Условия работы.
Последовательность расчета:
1. В зависимости от условий работы выбирают тип плоского ремня (см. занятие 35).
2. Определяют диаметр малого шкива по эмпирической формуле
D1= (520…610) (N1/ω1)1/3 мм, (Р.24)
где N1 - мощность на валу малого шкива в квт.
Размер D1 должен соответствовать ГОСТ 17383 — 72 (табл. Р.9).
3. Определяют скорость ремня о и сопоставляют ее с оптимальной для принятого типа ремня (см. занятие 35). При неудовлетворительной v изменяют D1.
4. Задаются коэффициентом скольжения ε и определяют диаметр большего шкива D1 [формула (Р.12)]. Полученный размер округляют до стандартного значения (табл. 9.9).
5. Уточняют передаточное число (формула Р.12).
6. Ориентировочно принимают межосевое расстояние А или в соответствии с требованием конструкции, или в рекомендуемых пределах (см. стр. 232).
7. Определяют расчетную длину ремня L [формула (Р.3)]. Для бесконечных ремней L округляют до стандартного значения.
8. Проверяют передачу на долговечность по числу пробегов ремня [формула (Р.23)] и, если оно выше допустимого, увеличивают длину ремня, т. е. принимают большее А.
9. Уточняют межосевое расстояние А [формула (Р.4)]. Расчет производят только для передач с бесконечным ремнем при окончательно установленной длине по стандарту.
10. Проверяют угол обхвата α1 ремнем малого шкива [формула (Р.5)] и при необходимости увеличивают межосевое расстояние А или применяют натяжной ролик.
11. Согласно рекомендациям (табл. 9.3) задаются отношением δ/D1 и определяют толщину ремня δ, округляя ее до ближайшего меньшего стандартного значения (табл. 9.1).
Определяют допускаемое приведенное полезное напряжение (допускаемое приведенное удельное окружное усилие) [kП] (см. табл. 9.3).
12. Находят поправочные коэффициенты Сα , Сv , Сp , Сθ и вычисляют допускаемое полезное напряжение [формула (Р.19)].
13. Вычисляют окружное усилие Р.
14. Из расчета по тяговой способности определяют требуемую площадь поперечного сечения ремня и его ширину b [формула (Р.22)], округляя до ближайшего большего стандартного значения (см. табл. 9.1 и др.). При несоответствии ширины b указанным в стандарте (для принятой толщины δ) производят перерасчет передачи.
15. Находят усилие предварительного натяжения ремня S0, [формула (Р.13)].
Пример 36. Рассчитать открытую плоскоременную передачу от электродвигателя к приводу поршневого водяного насоса. Мощность электродвигателя N1=4,5 квт; угловая скорость ω1 =78 рад/сек. Передаточное число i=3,16. Нагрузка с умеренными колебаниями, работа двухсменная. Угол наклона линии центров шкивов к горизонту θ=75o. Передачу выполнить с возможно меньшими габаритами.
Решение.
1. Учитывая повышенную влажность окружающей среды и желая получить недорогую передачу, принимаем прорезиненный ремень типа А.
2. Диаметр малого шкива [формула (Р..24)]
D1= (520…610) (N1/ω1)1/3 = (520…610) (4,5/78)1/3 = 200…266 мм.
По табл. 9.9 принимаем D1=200 мм.
3. Скорость ремня
.
Полученное значение скорости допустимо для прорезиненного ремня типа А (см. табл. 9.1).
4. Принимаем коэффициент скольжения ε=0,01. Диаметр большего шкива [формула (Р.12)]
D2=i D1 (1 - ε) = 3,16·200 (1 - 0,01) = 626 мм.
По табл. 9.9 (стр. 257) принимаем D2=630 мм.
5. Фактическое передаточное число
6. Исходя из требования получить возможно меньшие габариты передачи, принимаем межосевое расстояние [формула (Р.1)]
А=2(D2+D1)=2(630+200)=1660 мм.
7. Расчетная длина ремня [формула (Р.3)]
Прибавляем на сшивку ремня ΔL=242 мм. Общая длина ремня
L0 = L+ ΔL =4658+ 242 = 4900 мм.
8. Число пробегов ремня в секунду [формула (Р.23)]
,
что допустимо.
9. Уточнения межосевого расстояния не производим, так как ремень не бесконечный, а сшивной.
10. Угол обхвата ремнем малого шкива [формула (Р.5)]
.
11. Толщина ремня δ. По табл. 9.3 для прорезиненных ремней δ/D1 <= 1/40.
При D1=200 мм δ<= D1 /40 =200/40=5 мм.
По табл. 9.1 для ремня типа А принимаем толщину δ=4,5 мм (три прокладки с резиновыми прослойками).
Допускаемое приведенное полезное напряжение в ремне при σ0=1,76 н/мм2 (табл. 9.3).
[ko] = 2,45 - 9,81·δ/D1 = 2,45- 9,81·4,5/200 = 2,23 н/мм2 .
12. Поправочные коэффициенты:
по табл. 9,5 (интерполированием) Сα =0,957;
по формуле (Р.20) Сv= 1,04 - 0,0004v2 = 1,04 - 0,0004·7,82 = 1,02;
по табл. 9.6 (см. примечание) Сp =0,8;
по табл. 9.7 Сθ=0,9.
Допускаемое полезное напряжение [формула (Р.19)]
[kП] = [k0] Сα Сv Сp Сθ = 2,23· 0,957· 1,02 ·0,8· 0,9=1,56 н/мм2.
13. Окружное усилие
.
14, Площадь сечения F и ширина ремня b (формула Р.22):
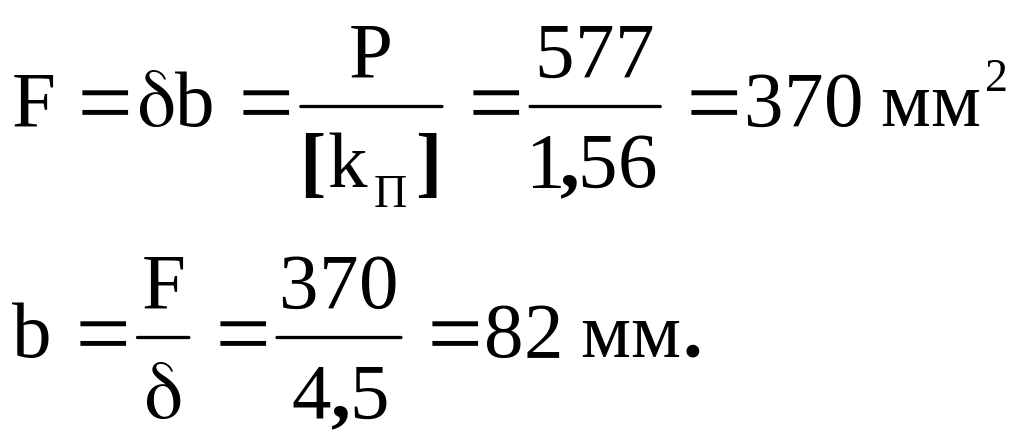
По табл. 9.1 принимаем b=85 мм.
15. Усилие предварительного натяжения ремня [формула (Р;13)]
So = Fσо= δbσо = 4,5· 85· 1,76 = 672 н.