Лекція 4.17. Декомпозиція задач і графи and/or
1. Представлення у формі І/Або-графів адекватне для задач, що природно розбиваються на взаємно незалежні підзадачи. Їхніми прикладами є пошук маршруту, символьне інтегрування, ігрові задачі, доказ теорем тощо.
Як приклад розглянемо задачу пошуку маршруту між двома заданими містами a та z згідно карті доріг.
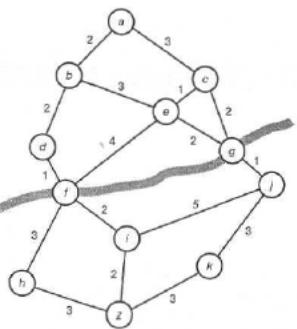
Рис. 1. Пошук маршруту
Не будемо поки враховувати довжину шляхів. Ясно, цю задачу можна сформулювати як пошук шляху в просторі станів, що співпадає із цією картою: вершини відповідають містам, дуги - шляхам між містами.
Розглянемо альтернативне подання, засноване на природній розбивці цієї задачі на підзадачі.
На наявній карті є також ріка, яка, нехай, обмежує переправу через неї лише по двох мостах: один у місті f, другий - у місті g. Тому маємо дві головні альтернативи:
щоб знайти шлях з а в z, необхідно знайти одне із двох:
шлях з а в z, що проходить через f, або
шлях з а в z, що проходить через g.
Тепер кожну із цих двох альтернативних задач можна, у свою чергу, розбити на підзадачі:
(1) Щоб знайти шлях з a в z через f, необхідно:
1.1 знайти шлях з а в f і
1.2 знайти шлях з f в z.
(2) Щоб знайти шлях з a в z через g, необхідно:
2.1 знайти шлях з а в g та
2.2 знайти шлях з g в z.
Отримана розбивка вихідної задачі відповідає формі малюнку І/Або-графа, напівкруглі дуги якого вказують на відношення І між відповідними підзадачами. Подальшу розбивку підзадач можна було б будувати на основі введення додаткових проміжних міст.
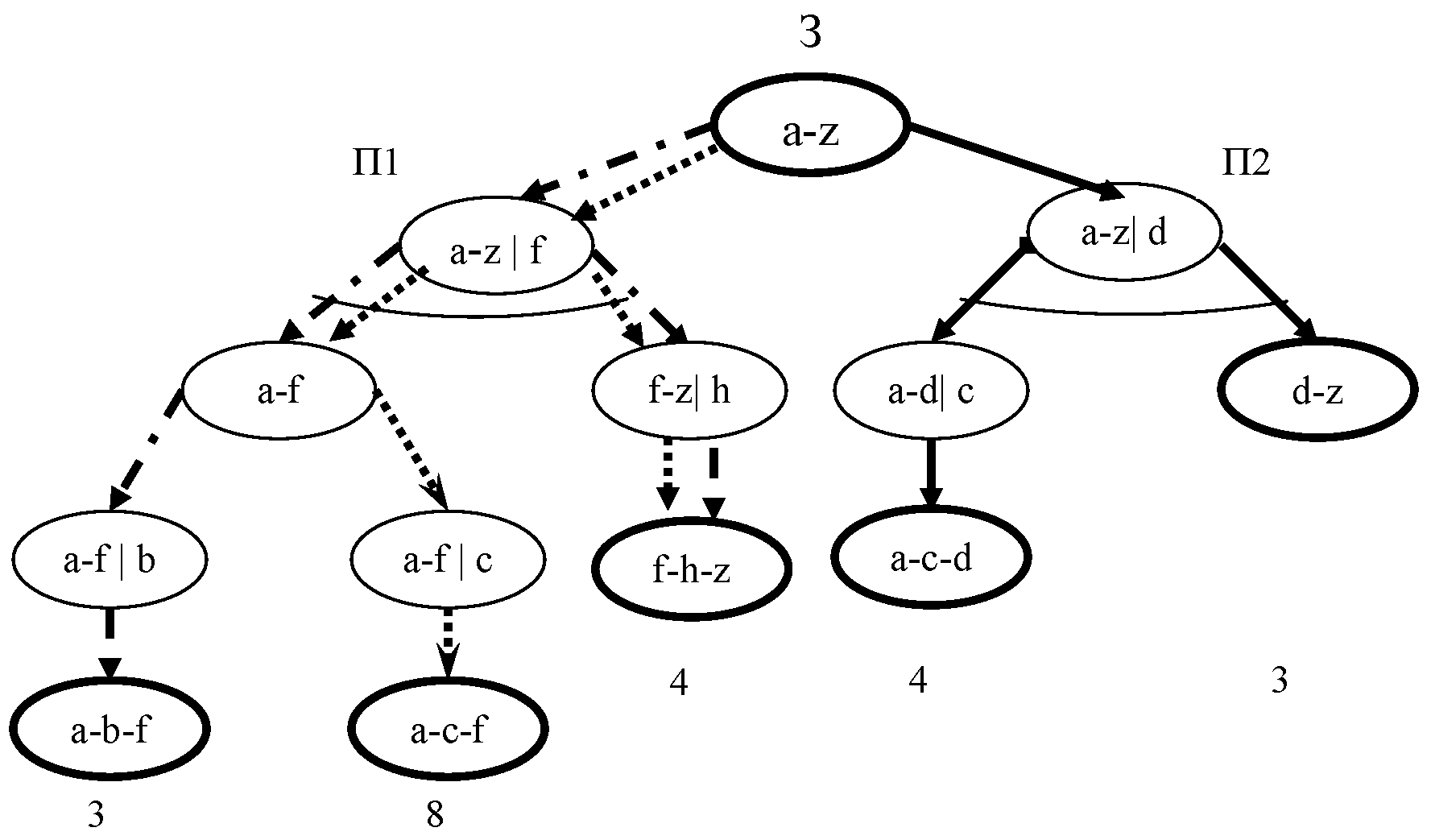Таким
чином, І/Або-Граф
- це спрямований граф, вершини якого
відповідають задачам, а дуги - відношенням
між задачами. Між дугами також існують
свої відншення. Це відношення І та АБО,
залежно від того, треба розв'язати тільки
одну із задач-спадкоємців або ж кілька
з них. Звичайно припускають, що кожна
вершина має або лише І-Спадкоємців, або
лише Або-Спадкоємців, оскільки в таку
форму можна перетворити будь-який
І/Або-Граф,
вводячи за необхідністю допоміжні
Або-вузли. Вузол, з якого виходять лише
І-Дуги, називають І-вузлом; вузол, з якого
виходять лише Або-Дуги, - Або-вузлом.
Коли задача представлялася у формі простору станів, її розв'язком був шлях у цьому просторі. У випадку І/Або-подання розв'язок повинний, містити всі підзадачи І-вузли. Отже, це вже не шлях, а дерево.
Вирішуюче дерево Т визначається в такий спосіб:
початкова задача Р - це корінь дерева Т;
якщо Р є Або-вузол, то в Т утримується тільки один з її спадкоємців ( з І/Або-Графа) разом зі своїм власним вирішуючим деревом;
якщо Р - це І-вузол, то в Т втримуються всі її спадкоємці (з І/Або-Графа) разом зі своїми вирішуючими деревами.
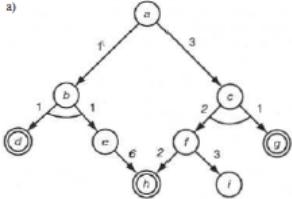
Ілюстрацією цього визначення може служити малюнок. Використовуючи вартості, можна формулювати критерії оптимальності розв'язку. Наприклад, можна визначити вартість вирішуючого графа як суму вартостей усіх його дуг. Тоді, в разі мінімізації вартості, треба обрати вирішуючий граф, зображений на малюнку (с).
Однак, не обов'язково вимірювати оптимальність рішення, базуючись на оцінках дуг. Іноді природнішим може стати приписувати вартість не дугам, а вузлам, або ж і тим, і іншим одночасно.
Рис. 2. Приклад І/Або-графа
Підсумуємо:
І/Або-подання засноване на декомпозиції задач до підзадач.
Вузли І/Або-графа відповідають задачам; зв'язки між вузлами - відношенням між задачами.
Вузол, з якого виходять Або-Зв'язки, називається Або-Вузлом. Для розв'язку задачі, позначеної Або-Вузлом, достатньо розв'язати одну з її задач-спадкоємців.
Вузол, з якого виходять І-Зв'язки, називається І-Вузлом. Для розв'язку відповідну задачі, позначеної І-Вузлом, потрібно розв'язати всі її задач-спадкоємці.
При заданому І/Або-графі конкретна задача формулюється завданням стартового вузла та цільової умови для розпізнавання цільових вузлів.
Цільові вузли (або "термінальні вузли") відповідають тривіальним (або "примітивним") задачам.
Розв'язок представляється у вигляді вирішуючого графа - підграфа всього І/Або-графа.
Подання задач у формі простору станів можна розглядати як спеціальний окремий випадок І/Або-подання, коли всі вузли І/Або-графа є Або-вузлами.
І/Або-подання має переваги тоді, коли вузли, що перебувають у відношенні І, представлені підзадачами, які можна вирішувати незалежно одна від одної.
Для формулювання критерію оптимальності розв'язку задачі можна приписати вартості дугам або вузлам, або і тим, і іншим.