Лекція 4.20.

ігри

Двох осіб з повною інформацією

1. Приклади: шахи, шашки тощо.

2. Участь двох гравців, що ходять по черзі та мають повну інформацію про поточну ігрову ситуацію.

3. Гра є кінченою по досягненні позиції, яка згідно до правил гри є "термінальною" (кінцевою) з фіксацією результату гри, наприклад матова позиція в шахах.

4. Можливе подання у формі дерева гри (або ігрового дерева), чиї вершини фіксують ситуації (коренева вершина - початкова ситуація, листи - термінальні позиції), а дуги - ходи.

5. Обмежуються лише двома типами результатів - виграш і програш.

6. Два учасники гри "гравець" і "супротивник":

• гравець може виграти в деякій нетермінальній позиції з ходом гравця ("позиції гравця"), якщо в ній існує дозволений хід, що веде до виграшу;

• з іншого боку, деяка нетермінальна позиція з ходом супротивника ("позиція супротивника") є виграною для гравця, якщо всі дозволені ходи із цієї позиції ведуть до позицій, у яких можливий виграш.

Ці правила повністю відповідають поданню задач у формі І/Або-дерева. Між поняттями щодо І/Або-дерева і поняттями ігор існує взаємно однозначна відповідність:

позиції гри вузли, вершини, задачі

термінальні позиції цільові вузли,

виграшу тривіально розв'язувані задачі

термінальні позиції задачі, що не мають

програшу рішення

виграні позиції задачі, що мають рішення

позиції гравця Або-вузли

позиції супротивника І-вузли

Вочевидь, що й поняття щодо пошуку в І/Або-деревах можна визначити в термінах пошуку в ігрових деревах.

Нижче наведено просту програму, що визначає, чи є деяка позиція виграною для гравця.

вигр(Поз) :-

         терм_вигр( Поз). % Термінальна виграна позиція

вигр(Поз) :- not терм_прогр(Поз),

         хід(Поз, Поз1),    % Дозволений хід в Поз1

         not (хід(Поз1, Поз2),

         not вигр( Поз2) ). % Жоден з ходів супротивника

не веде до не-виграшу

Тут правила гри вбудовані в предикат хід(Поз, Поз1), що породжує всі дозволені ходи, а також у предикати терм_вигр(Поз) і терм_прогр(Поз), які розпізнають термінальні позиції, що є, відповідно до правил гри, виграними або програними.

1. Ця програма використає стратегію вглиб та демонструє основні принципи програмування ігор.

2. Але практично прийнятна реалізація таких складних ігор, як шахи або го, вимагала б залучення значно могутніших методів.

3. Величезна комбінаторна складність цих ігор робить наївний перебірний алгоритм, що переглядає дерево аж до термінальних позицій, абсолютно непридатним.

4. Цей висновок ілюструє (на прикладі шахів) рис. 1: простір пошуку має астрономічні розміри - близько 10¹²⁰ позицій, що перебуває далеко за межами можливостей комп’ютерів.

Рис. 1. Складність ігрових дерев у шахах. Оцінки згідно тому, що: а) в кожній шаховій позиції існує приблизно 30 дозволених ходів; б) термінальні позиції розташовані на глибині у 40 ходів. Один хід включає два напівходи - по одному на кожного гравця.

2. Мінімаксний принцип є стандартним у пошуку в ігрових (особливо в шахових) програмах:

• Дерево гри проглядається лише до деякої глибини (звичайно на кілька ходів), а потім для всіх його кінцевих вершин обчислюються оцінки згідно до деякої оцінюючої функції.

• Далі оцінки кінцевих вершин поширюються нагору по дереву пошуку згідно до мінімаксного принципу. У результаті всі вершини дерева пошуку одержують оцінки.

• І нарешті, ігрова програма, що бере участь у деякій грі, робить свій хід - той, що веде з початкової позиції в найперспективнішого (за оцінкою) її спадкоємця.

Тут використано два різних об’єкти - "дерево гри" і "дерево пошуку": дерево пошуку - це лише частина дерева гри (його верхня частина), тобто та його частина, що була явно породжена в процесі пошуку.

• Дуже багато залежить від оцінюючої функції шансів на виграш одного з учасників гри.

• Чим вища оцінка, тим більше шансів на виграш у гравця, і чим вона нижча, тим більше шансів на виграш у супротивника.

• Оскільки один з учасників гри завжди прагне до високих оцінок, а інший - до низьких, їх іменують МАКС і МІН відповідно. МАКС завжди обирає хід з максимальною оцінкою, а МІН - хід з мінімальною оцінкою.

Керуючись мінімаксним принципом і знаючи значення оцінок для всіх вершин "підніжжя" дерева пошуку, можна визначити оцінки всіх інших вершин дерева. На рис. 2 показано, як це робиться крізь пари рівнів позицій з ходом Макс'а та з ходом Мін'а:

• Оцінки вершин найнижчого рівня визначаються за допомогою оцінюючої функції.

• Оцінки внутрішніх вершин визначаються, рухаючись знизу нагору від рівня до рівня, аж до кореня дерева.

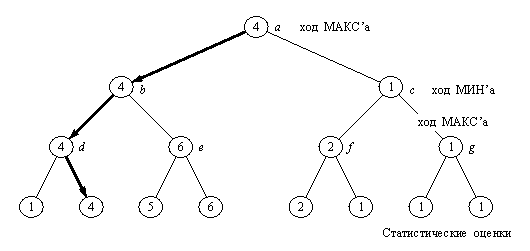
Рис. 2. Статичні (нижній рівень) і мінімаксні оцінки вершин дерева пошуку. Виділені ходи фіксують основний варіант, тобто мінімаксно-оптимальну гру по обидва боки.

У результаті, згідно прикладу (рис. 2), оцінка кореня стає рівною 4, і, відповідно, з позиції а кращим ходом Макс'а буде a-b. Краща відповідь Мін'а на цей хід - b-d, і т.д. Цю послідовність ходів називають основним варіантом, який показує "мінімаксно-оптимальну" гру для обох учасників.

Звичайно розрізняють два види оцінок: оцінки вершин нижнього рівня й оцінки внутрішніх вершин (робочі оцінки). Перші називають також "статичними", тому що обчислюються згідно до "статичної" оцінюючої функції, на противагу робочим оцінкам, одержуваним "динамічно" поширенням статичних оцінок нагору по дереву.

Правила поширення оцінок формулюють в такий спосіб. Статичну оцінку позиції Р позначають через v(P), а її робочу оцінку - через V(Р). Нехай Р₁, ..., Р_n - дозволені спадкоємці позиції Р. Тоді співвідношення між статичними й робочими оцінками можна записати так:

V( Р) = v( P),

якщо Р - термінальна позиція дерева пошуку (n=0).

V(Р) = max V(Р_і ),

і

якщо P - позиція з ходом Макс'а.

V(Р) = mіn V(Р_і ),

і

якщо Р - позиція з ходом Мін'а.

Спрощена реалізація мінімаксного принципу

% Мінімаксна процедура: мінімакс(Поз,КращаПоз,Оц)

% Поз - позиція, Оц - її мінімаксна оцінка;

% кращий хід з Поз веде в позицію КращаПоз

% СписПоз - список дозволених ходів

мінімакс(Поз, КращаПоз, Оц) :-    ходи(Поз,СписПоз),!, кращ(СписПоз,КращаПоз,Оц);     стат_оц( Поз, Оц).         % Поз не має спадкоємців

кращ( [Поз], Поз, Оц) :- мінімакс( Поз, _, Оц),  !.

кращ( [Поз1 | СписПоз], КращаПоз, КращаОц) :-      мінімакс( Поз1, _, Оц1),кращ( СписПоз, Поз2, Оц2),      вибір( Поз1, Оц1, Поз2, Оц2, КращаПоз, КращаОц).

вибір( Поз0, Оц0, Поз1, Оц1, Поз0, Оц0) :-      хід_міна(Поз0), Оц0>Оц1, !; %обирається кращою

позиція Поз0, якщо вона є позицією з ходом Мін'а

хід_макса(Поз0),Оц0<Оц1,!. %обирається кращою

позиція Поз0, якщо вона є позицією з ходом Макс'а

вибір( Поз0, Оц0, Поз1, Оц1, Поз1, Оц1).

Основне відношення програми, що обчислює мінімаксну робочу оцінку для деякої заданої позиці -

        мінімакс( Поз, КращаПоз, Оц)

де Оц  -  мінімаксна оцінка позиції Поз, а КращаПоз - найкраща позиція-спадкоємець позиції Поз (кращий хід, що дозволяє досягти оцінки Оц). Відношення

        ходи( Поз, СписПоз)

задає дозволені ходи гри у списку СписПоз дозволених позицій-спадкоємців позиції Поз. Вважається, що ціль ходи неуспішна, якщо Поз є термінальною пошуковою позицією (листом дерева пошуку). Відношення

        кращ( СписПоз, КращаПоз, КращаОц)

обирає зі списку позицій-кандидатів СписПоз "найкращу" позицію КращаПоз. КращаОц - оцінка позиції КращаПоз, а отже, і позиції Поз. Під "найкращою" оцінкою розуміють або максимальну, або мінімальну оцінку, залежно від того, із чиєї сторони очікується хід.

3. Альфа-бета-алгоритм: ефективна реалізація принципу мінімакса

• Перегляд дерева пошуку вглиб, проглядаючи всі можливі позиції, аж до термінальних з обчисленням статичних оцінок всіх термінальних позицій.

• Як правило, для одержання вірної мінімаксної оцінки кореневої вершини, цю роботу не обов'язково проробляти повністю.

• Тому алгоритм пошуку можна вдосконалити, використавши наступну ідею.

Нехай, є два варіанти ходу. Довідавшись, що один з них явно гірший іншого, можна прийняти вірне рішення, не з'ясовуючи, наскільки він гірший.

Використаймо цей принцип для скорочення дерева пошуку рис.2. Процес пошуку протікає в такий спосіб:

(1) Почати з позиції а.

(2) Перейти вниз до позиції b.

(3) Перейти вниз до позиції d.

(4) Вибрати максимальну з оцінок спадкоємців позиції d, що дає V(d) = 4.

(5) Повернення до позиції b і далі спуск вниз до позиції е.

(6) Отримаємо оцінку 5 першого спадкоємця позиції е, згідно до якої для МАКСа (який має ходити в позиції е) гарантована оцінка не менша, чим 5, незалежно від оцінок інших (можливо, кращих) варіантів ходу. Цього цілком достатньо, щоб МІН, навіть не знаючи точної оцінки позиції е, в позиції b обрав саме хід в d.

На підставі наведеного можна приписати е наближену оцінку 5. Наближений характер цієї оцінки не зробить ніякого впливу на оцінку позиції b, а отже, і позиції а.

На цій ідеї заснований знаменитий альфа-бета алгоритм щодо ефективної реалізації мінімаксного принципу. Результат його застосування до дерева рис. 2 показано на рис. 3, з якого видно, що деякі з робочих оцінок стали наближеними. Однак їх вистачило для точної оцінки кореневої позиції при зменшенні складності пошуку (відносно первісного дерева пошуку рис. 2) з восьми до п'яти звернень до оцінюючої функції.

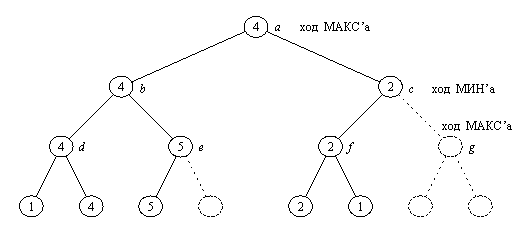
Рис. 3. Дерево рис. 2 після застосування альфа-бета алгоритму. Пунктиром показано гілки, відсічені альфа-бета алгоритмом для економії обсягу пошуку. У результаті деякі з робочих оцінок стали наближеними, однак це не завадило обчисленню точної оцінки кореневої вершини й побудови основного варіанта.

Отже, ключова ідея альфа-бета відсікання полягає в пошуку не обов'язково кращого, але "досить гарного" ходу для прийняття вірного рішення.

Формалізують ідею два граничних значення Альфа і Бета, між якими має бути робоча оцінка позиції:

• Альфа - це найменше значення оцінки, яке на цей момент гарантовано для гравця МАКС;

• Бета - це найбільше значення оцінки, на яке МАКС поки ще може сподіватись. Звісно, з погляду Мін'а, Бета є найгіршою гарантованою для нього оцінкою.

• Отже, дійсне значення оцінки (яке потрібно знайти) завжди лежить між Альфа і Бета.

• Якщо ж стало відомо, що оцінка деякої позиції лежить поза інтервалом Альфа-Бета, то цього досить для висновку: дана позиція не входить в основний варіант. При цьому не потрібне точне значення оцінки такої позиції, його треба знати лише тоді, коли оцінка лежить між Альфа і Бета.

• "Досить гарну" робочу оцінку V(Р, Альфа, Бета) позиції Р можна визначити формально як будь-яке значення, що задовольняє наступним обмеженням:

V( P, Альфа, Бета) <= Альфа якщо V( P) <= Альфа

V( P, Альфа, Бета) = V( P) якщо Альфа < V( P) < Бета

V( P, Альфа, Бета) >= Бета якщо V( P) >= Бета

Вочевидь, що, вміючи обчислювати "досить гарну" оцінку, завжди можна обчислити точну оцінку кореневої позиції Р, встановивши границі інтервалу в такий спосіб:

V( Р, - нескінченність, + нескінченність) = V( P)

Нижче наведено реалізацію альфа-бета алгоритму у формі програми Прологу. Тут основне відношення –

альфабета(Поз, Альфа, Бета, ХорПоз, Оц)

де ХорПоз - спадкоємець позиції Поз із "досить гарною" оцінкою Оц, що задовольняє всім вказаним обмеженням:

Оц = V( Поз, Альфа, Бета)

Процедура

прибл_кращ( СписПоз, Альфа, Бета, ХорПоз, Оц)

знаходить досить гарну позицію ХорПоз у списку позицій СписПоз; Оц - наближена (стосовно Альфа і Бета) робоча оцінка позиції ХорПоз. Інтервал між Альфа і Бета може звужуватись (але не розширюватись!) у міру заглиблення пошуку при рекурсивних зверненнях до альфа-бета процедури. Відношення

нов_границі(Альфа,Бета,Поз,Оц,НовАльфа,НовБета)

визначає новий інтервал (НовАльфа,НовБета), завжди вужчий за старий (Альфа, Бета), або дорівнює йому. Так що, чим глибше заглиблюємось в дереві пошуку, тим сильніше стискається інтервал Альфа-Бета, і в результаті оцінювання позицій на глибших рівнях відбувається за вужчих границь. При більш вузьких інтервалах допускається більша "приблизність" в обчисленні оцінок, а отже, відсікається більше гілок дерева.

Виникає цікаве питання: наскільки великою є економія, що досягається альфа-бета алгоритмом порівняно із програмою мінімаксного повного перебору рис. 2?

Ефективність альфа-бета процедури залежить від порядку, у якому проглядаються позиції. Завжди краще першими розглядати найсильніші ходи з кожної з сторін.

% Альфа-бета алгоритм

альфабета(Поз,Альфа,Бета,ХорПоз,Оц):-

ходи(Поз,СписПоз),!,

прибл_кращ(СписПоз,Альфа,Бета,ХорПоз,Оц);

стат_оц(Поз,Оц).

прибл_кращ([Поз|СписПоз],Альфа,Бета,ХорПоз,ХорОц):-

альфабета(Поз,Альфа,Бета,_,Оц),

дост_хор(СписПоз,Альфа,Бета,Поз,Оц,ХорПоз,ХорОц).

дост_хор([ ],_,_,Поз,Оц,Поз,Оц):- !. %Больш нема кандидатів

дост_хор(_,Альфа,Бета,Поз,Оц,Поз,Оц):-

хід_міна(Поз),Оц>Бета,!; %Перехід через верхню гран

хід_макса(Поз),Оц<Альфа,!. %Перехід через нижню гран

дост_хор(СписПоз,Альфа,Бета,Поз,Оц,ХорПоз,ХорОц):-

нов_границі(Альфа,Бета,Поз,Оц,НовАльфа,НовБета), % Уточнює границі

прибл_кращ(СписПоз,НовАльфа,НовБета,Поз1,Оц1), вибір(Поз,Оц,Поз1,Оц1,ХорПоз,ХорОц).

нов_границі(Альфа,Бета,Поз,Оц,Оц,Бета):-

хід_міна( Поз),Оц>Альфа,!. %Збільшує нижню границю

нов_границі(Альфа,Бета,Поз,Оц,Альфа,Оц):-

хід_макса(Поз),Оц<Бета,!. % Зменшує верхню границю

нов_границі(Альфа,Бета,_,_,Альфа,Бета).

вибір(Поз,Оц,Поз1,Оц1,Поз,Оц):-

хід_міна(Поз),Оц>Оц1,!;

хід_макса(Поз),Оц<Оц1,!.

вибір(_,_,Поз1,Оц1,Поз1,Оц1).

Відомо, що в найгіршому випадку альфа-бета алгоритм не має ніяких переваг відносно мінімаксного алгоритму повного перебору.

Однак, якщо порядок перегляду виявиться вдалим, то економія може бути значною.

Цей факт має практичний аспект стосовно турнірів ігрових програм. Шаховій програмі, що бере участь у турнірі, звичайно дається певний час для обчислення чергового ходу, і доступна програмі глибина пошуку залежить від цього часу.

Порівняно з мінімаксним повним перебором альфа-бета алгоритм зможе пройти при пошуку вдвічі глибше, а досвід показує, що застосування тої ж самої оцінюючої функції, але на більшій глибині приводить до більш сильної гри.

Економію, одержувану за рахунок застосування альфа-бета алгоритму, можна також виразити в термінах більш ефективного коефіцієнта розгалуження дерева пошуку (тобто числа гілок, що виходять із кожної внутрішньої вершини).

У шахових програмах, що використають альфа-бета алгоритм, досягається коефіцієнт розгалуження, рівний 6, при наявності 30 різних варіантів ходу в кожній позиції. Втім, на цей результат можна подивитися й менш оптимістично: незважаючи на застосування альфа-бета алгоритму, після кожного просування вглиб на один напівхід число термінальних пошукових вершин збільшується приблизно в 6 разів.