Несбалансированные транспортные задачи.

Как уже отмечалось выше, эффективные методы решения транспортной задачи применимы только при условии, что она сбалансирована, т.е. если сумма запасов, которые поставщики хотят вывезти, равна сумме заказов потребителей. Естественно, что на практике транспортные задачи оказываются гораздо сложнее. Сумма запасов может превышает сумму заказов (излишек запасов) или, наоборот, сумма запасов может быть меньше, чем сумма заказов (дефицит запасов).

В первом случае часть запасов, очевидно, должна остаться на складах поставщиков, и дополнительный вопрос при этом состоит в том, сколько грузов не вывозить (оставить на складе) у каждого поставщика, чтобы сумма транспортных издержек при выполнении заказов потребителей была бы минимальной.

Во втором случае предстоит решать, как распределить дефицит между потребителями. Разумеется, в реальности этот случай сложнее для менеджера, отвечающего за доставку заказов потребителям. Решение проблемы будет, по-видимому, определяться приоритетом каждого из потребителей для поставщика или исходом переговоров. Однако, если предположить, что все потребители имеют одинаковый рейтинг и проблема состоит только в том, чтобы подешевле развезти весь имеющийся на складах поставщика товар, то этот второй случай с точки зрения оптимизации издержек симметричен первому. Рассмотрим оба случая.

Несбалансированность: излишек запасов.

Рассмотрим этот случай сначала на примере решения способом, рассмотренным выше.

Пример 2

Пусть требуется минимизировать затраты на перевозку товаров от 3 предприятий-производителей на торговые склады 5 городов, куда необходимо поставить 180, 80, 200, 160 и 220 единиц товара соответственно. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей и затраты на перевозку единицы товара.

Заводы	Поставки	Склад 1	Склад 2	Склад 3	Склад 4	Склад 5
Завод 1	310	10	8	6	5	4
Завод 2	260	6	5	4	3	6
Завод 3	280	3	4	5	5	9

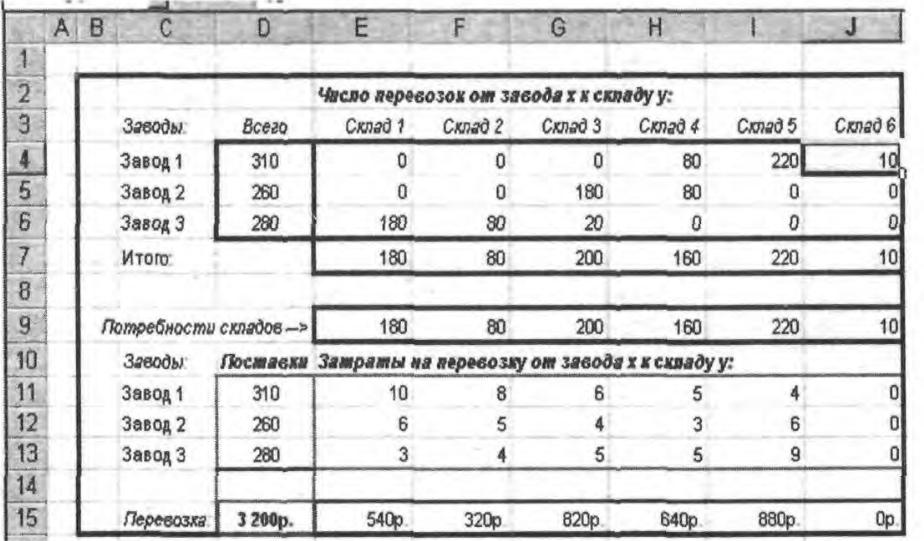
Как видно из таблицы, заводы могут поставить 850 единиц товара, а суммарная потребность составляет 840.

Решение.

1. Организуем данные задачи, как показано на рис.

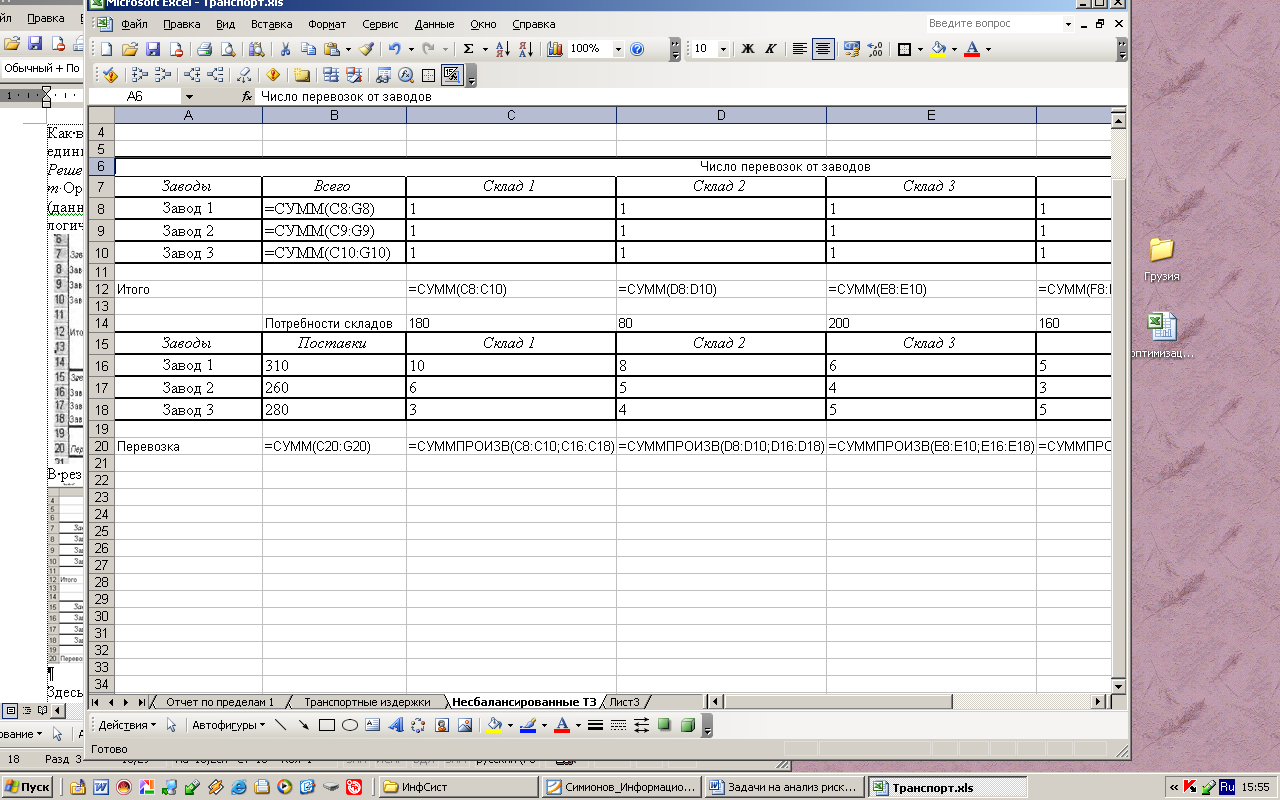
В результате модель будет иметь вид

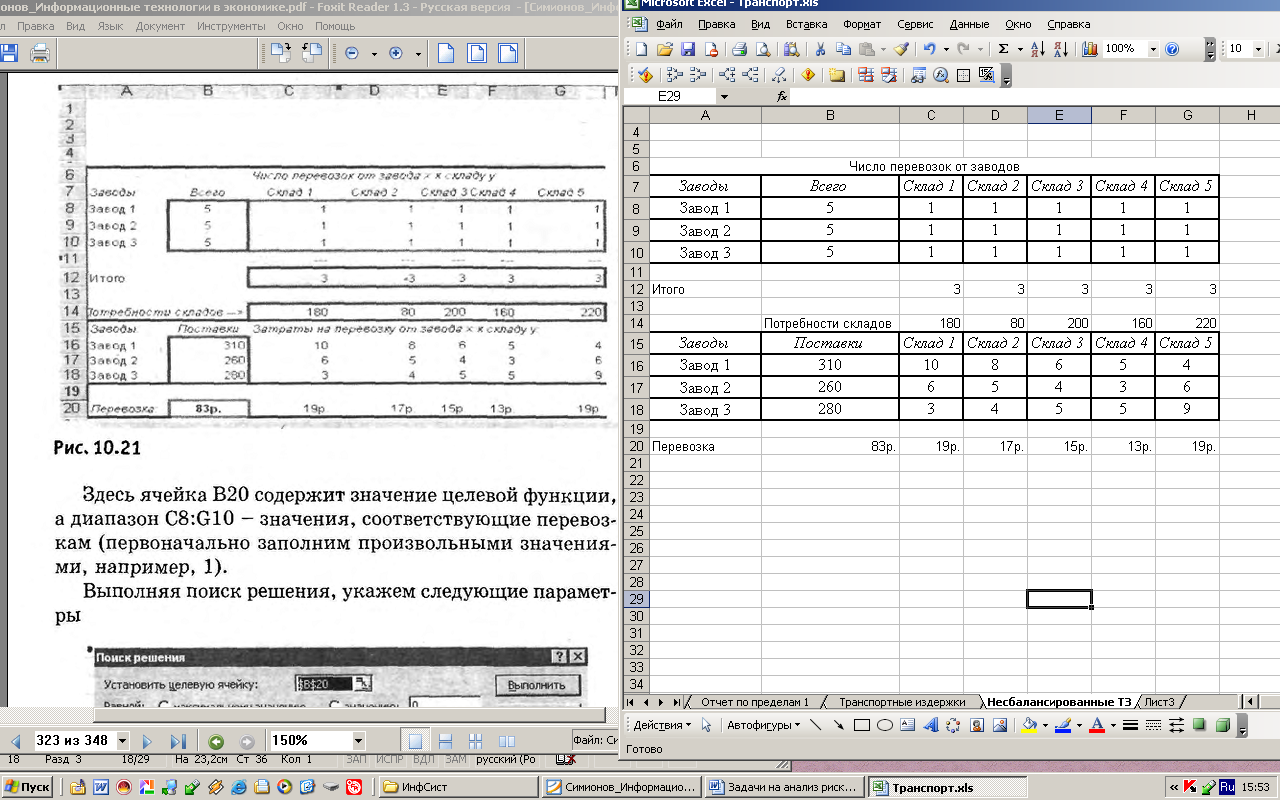
Здесь ячейка В20 содержит значение целевой функции, а диапазон C8:G10 - значения, соответствующие перевозкам (первоначально заполним произвольными значениями, например, 1).

2. Выполняя поиск решения, укажем следующие параметры

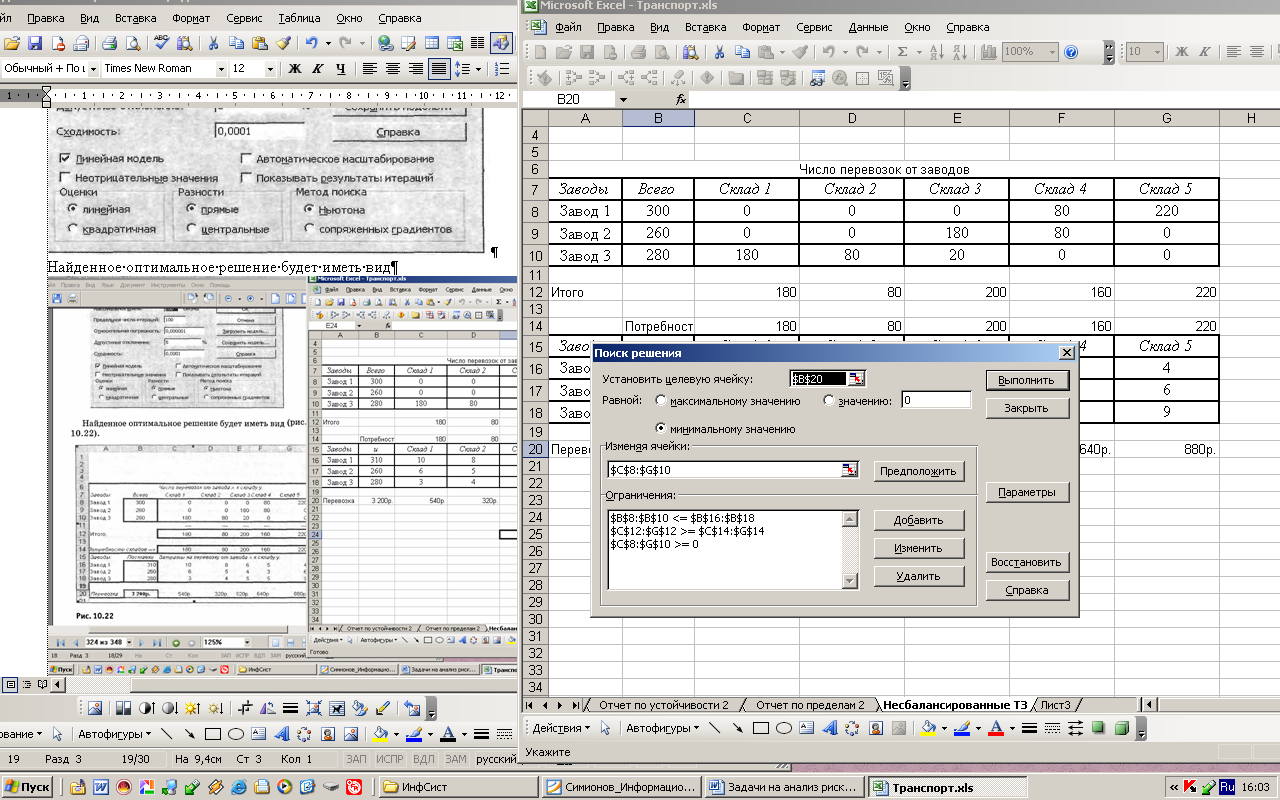
Найденное оптимальное решение будет иметь вид

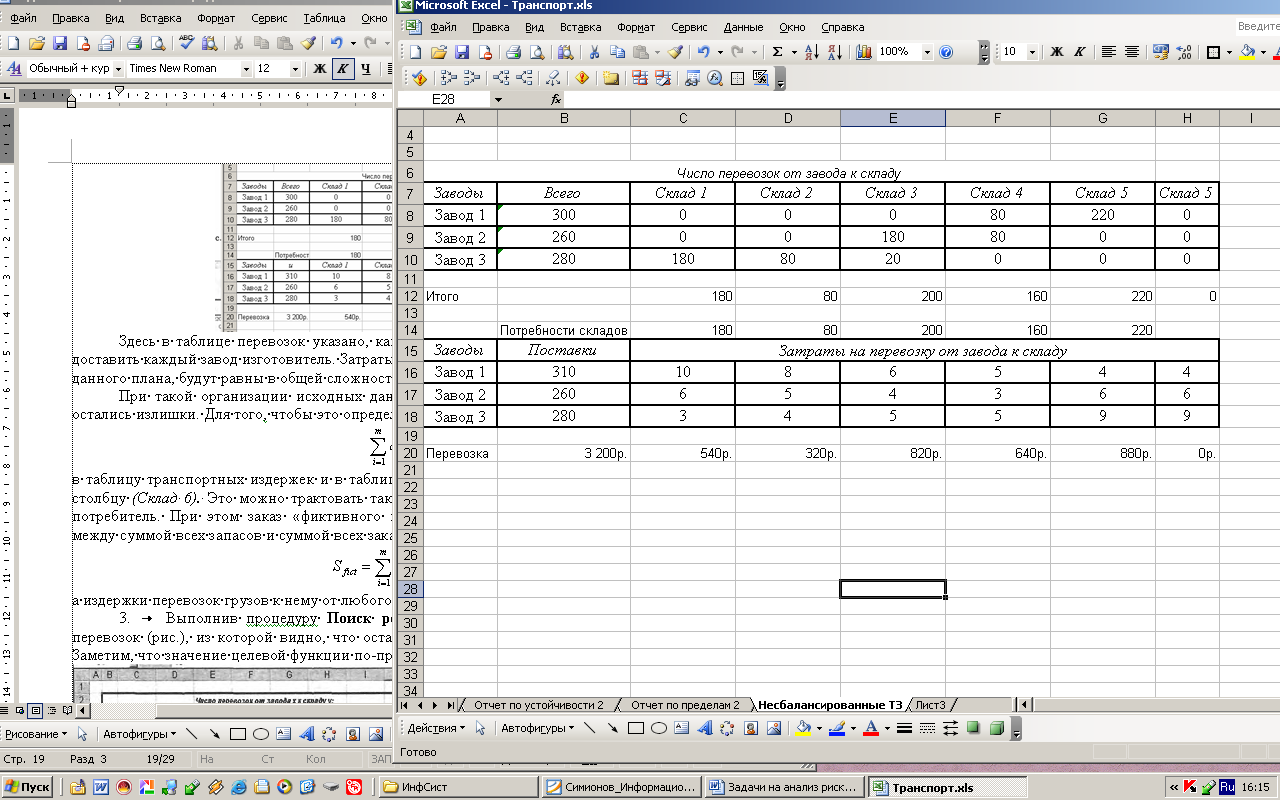
Здесь в таблице перевозок указано, какое количество товара на какой склад должен доставить каждый завод изготовитель. Затраты, которые будут иметь место при реализации

данного плана, будут равны в общей сложности 3 200р.

При такой организации исходных данных явно не определяется, на каких складах остались излишки. Для того, чтобы это определить, в случае излишка запасов, т.е. когда

в таблицу транспортных издержек и в таблицу перевозок добавляется по одному лишнему столбцу (Склад 6). Это можно трактовать так, как если бы появился еще один, фиктивный, потребитель. При этом заказ «фиктивного потребителя» в точности равняется разности между суммой всех запасов и суммой всех заказов

а издержки перевозок грузов к нему от любого поставщика равняются нулю.

3. Выполнив процедуру Поиск решения, получим результат в виде таблицы перевозок (рис.), из которой видно, что остаток товара в 10 единиц будет иметь Завод 1. Заметим, что значение целевой функции по-прежнему равно 3 200р.