Анализ оптимального решения
Модели оптимизации в реальных задачах могут содержать очень много переменных и параметров, которые невозможно эффективно корректировать без специального исследования. Числовые характеристики модели меняются в зависимости от внешних условий и зачастую достаточно быстро. В этой связи анализ устойчивости оптимального плана играет особую роль в организации управления экономическими объектами, принятии решений в критических ситуациях. Оказывается, что существует определенный интервал устойчивости, в котором изменение целевых коэффициентов не приводит к изменению оптимального решения. В границах этого интервала можно без риска для прибыли целенаправленно менять значения параметров.
Отчет по устойчивости.
В процессе поиска оптимального решения MS Excel формирует по желанию пользователя отчеты по результатам, по устойчивости и по пределам. Для вывода отчетов в окне Результаты поиска решения следует указать типы нужных отчетов: «Результаты», «Устойчивость» и/или «Пределы». В результате MS Excel создаст дополнительные листы «Отчет по результатам», «Отчет по устойчивости» и «Отчет по пределам», анализируя которые, пользователь может подобрать такие параметры модели, которые наилучшим образом соответствуют эффективной организации производства (рис.4-6).
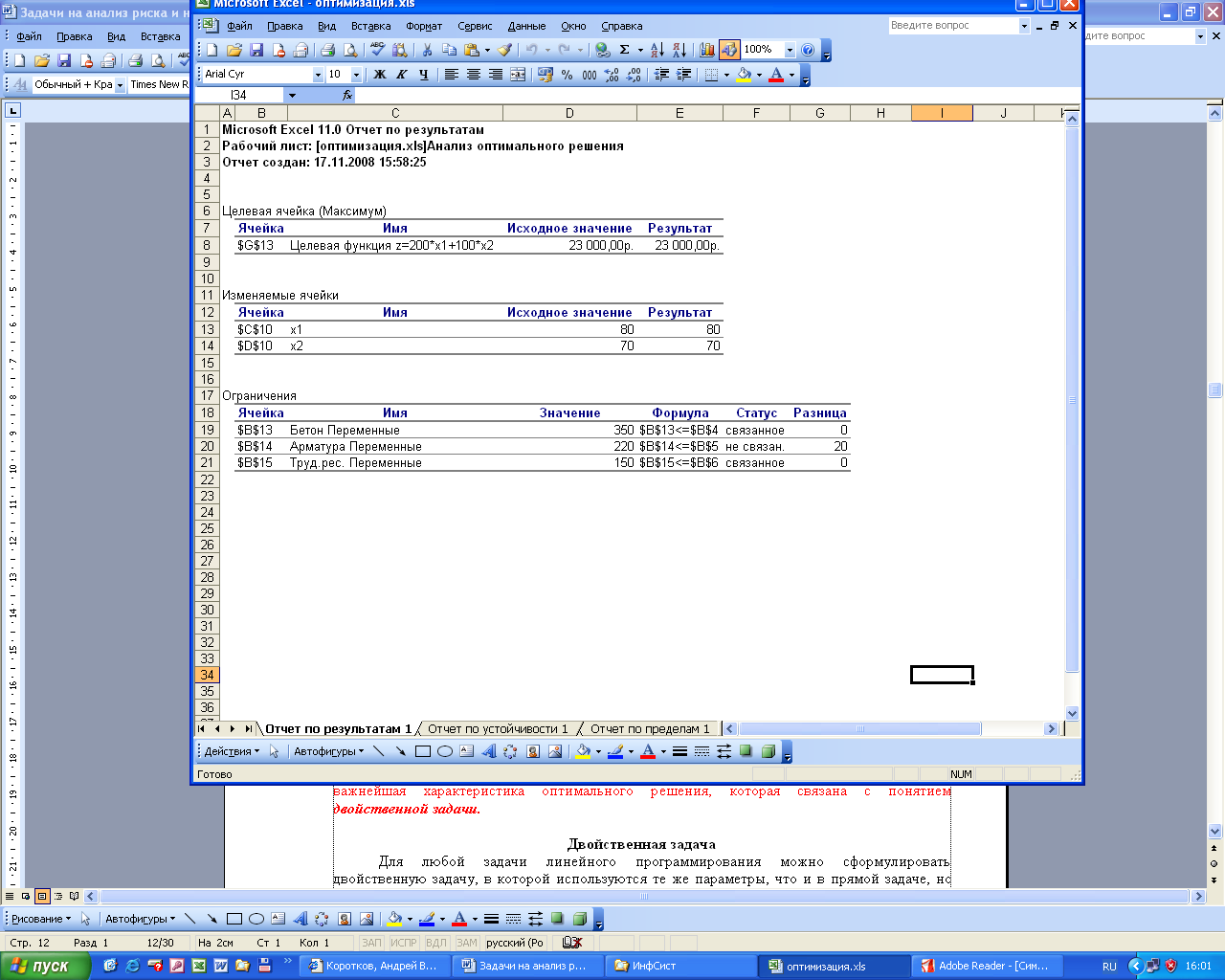
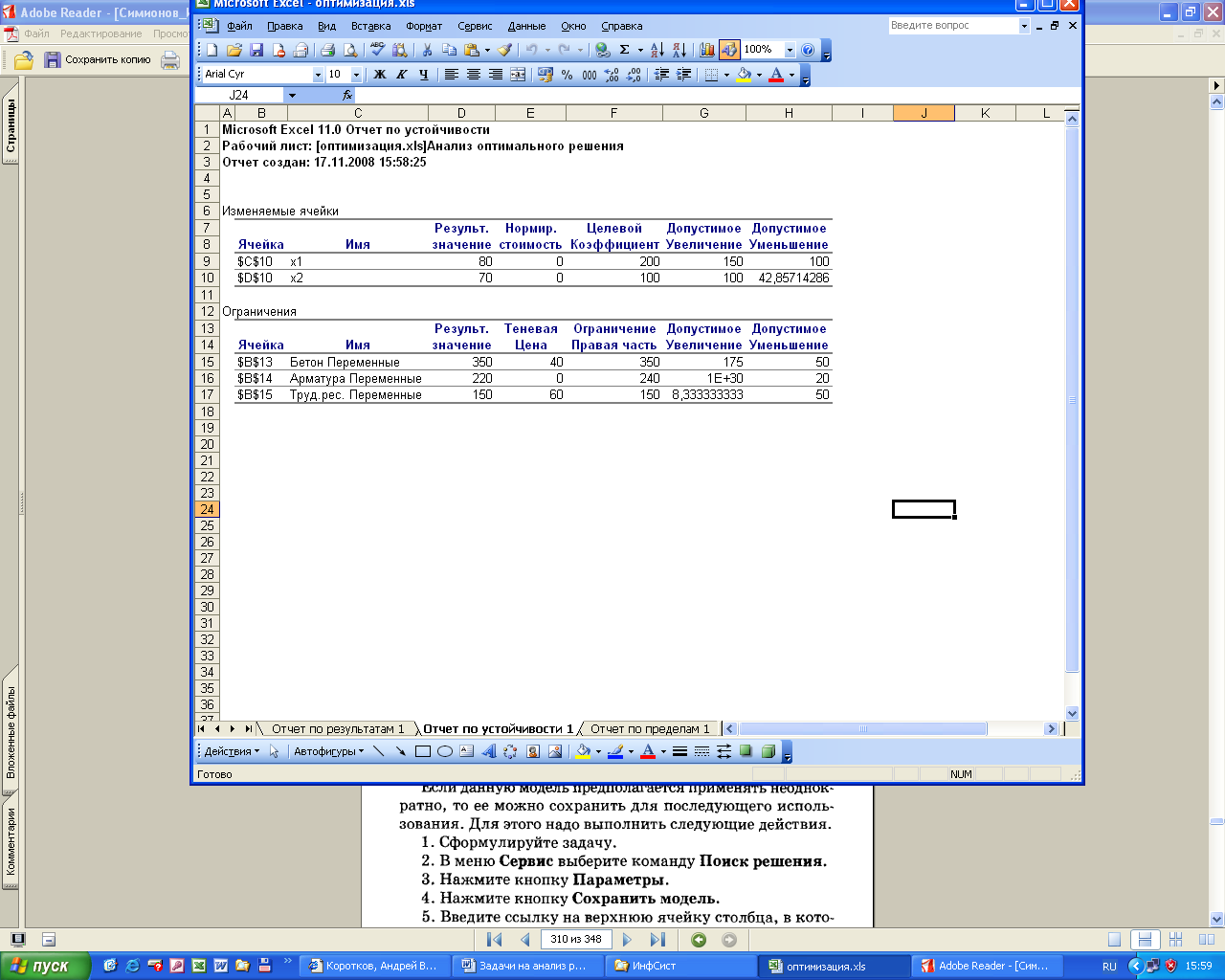
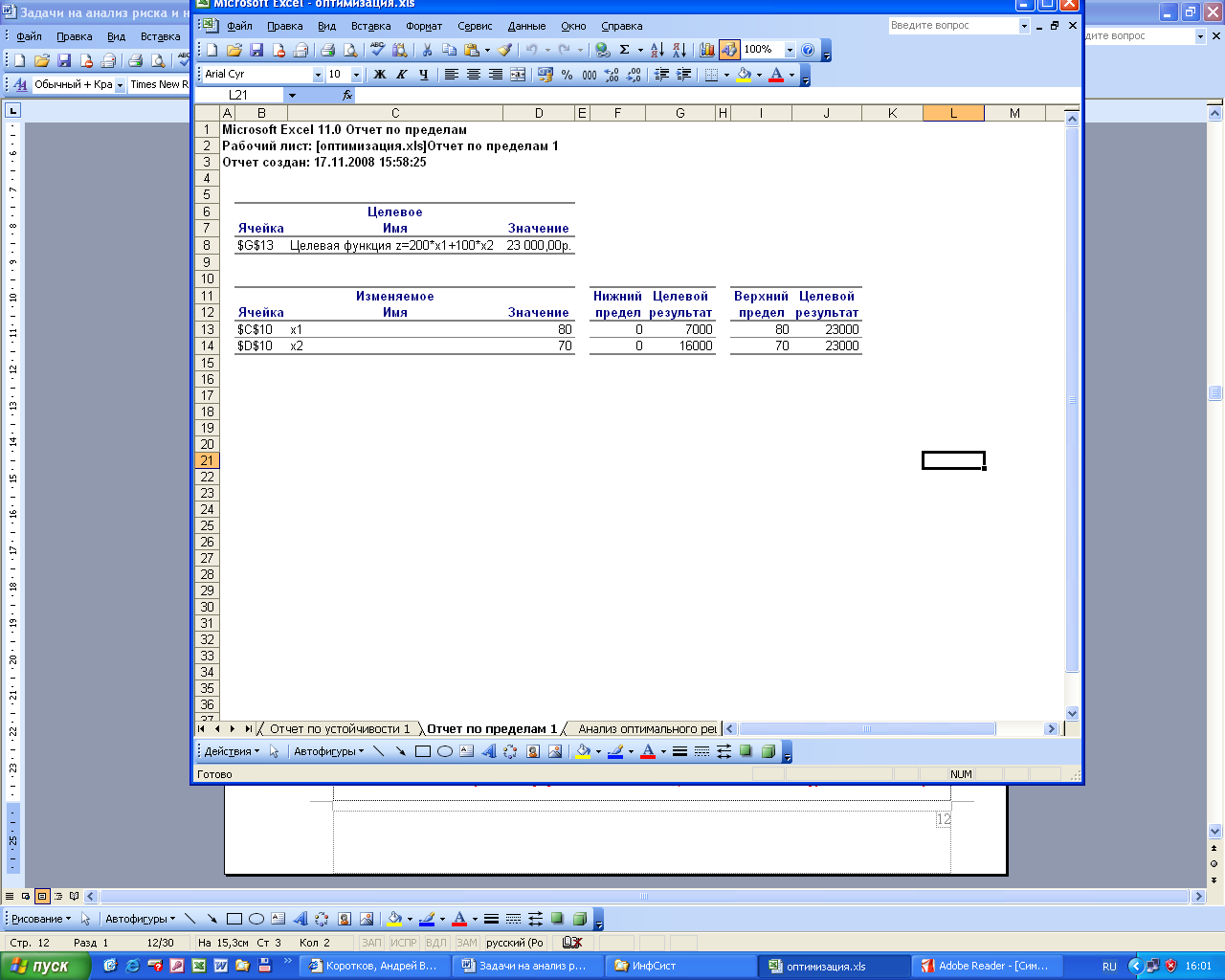
Рис.4-6
В отчете по устойчивости первая таблица «Изменяемые ячейки» содержит информацию о диапазоне изменения целевых коэффициентов, в пределах которого оптимальные значения переменных не меняются. Так, например, коэффициент при переменной x1, равный в модели 200 может быть увеличен на 150 (до 350), а коэффициент при x2, — на 100 (до 200). Аналогично эти коэффициенты могут быть уменьшены на 100 и 42,8 соответственно. При этом меняется значение целевой функции, что можно использовать при решении вопроса повышения прибыли (рис.7).
Рис.7
В таблице «Ограничения» отчета об устойчивости установлены границы диапазона для величины ресурсов. При варьировании ограничений на ресурсы в указанном диапазоне оптимальный план будет непрерывно изменяться (значение целевой функции также будет меняться), однако при этом будет оставаться неизменной теневая цена ресурса — важнейшая характеристика оптимального решения, которая связана с понятием двойственной задачи.
Двойственная задача
Для любой задачи линейного программирования можно сформулировать двойственную задачу, в которой используются те же параметры, что и в прямой задаче, но которая формулируется симметрично относительно переменных-ограничений. Предположим, что требуется узнать, при каких ценах на ресурсы, используемые для производства бетонных изделий (см. таблицу «Параметры задачи»), будет выгоднее продать эти ресурсы, чем производить из них продукцию? Какую минимальную сумму можно получить в виде прибыли от продажи ресурсов? Построим модель данной задачи. Обозначим через y1, y2, y3. Цены на единицу бетона, арматуры и стоимость труда за один рабочий день. Такие цены характеризуют степень ценности ресурса для производителя и называются теневыми ценами. Целевая функция — это с одной стороны прибыль, которая может быть получена от продажи
сех ресурсов по данным ценам. Она равна сумме произведений цен на значение запаса соответствующего ресурса. Но с точки зрения покупателя ресурсов значение целевой функции — это его издержки, которые желательно сделать как можно меньше (купить дешевле). То есть значение целевой функции требуется минимизировать. Что касается ограничений задачи, то здесь необходимо учесть, что производитель стремится продать ресурсы по таким ценам, чтобы прибыль была не меньше той, которую он получил бы при производстве продукции из этих ресурсов. Таким образом, например, ему надо продать 3,5 куб.м. бетона, 1 упаковку арматуры и 1 день труда в сумме не меньше, чем прибыль от производства одного лестничного марша. То есть должно выполниться ограничение:
3,5y1+y2+y3 200.
На рис. представлена модель двойственной задачи.
Для нахождения решения в окне Поиск решения необходимо установить переключатель на минимальное значение, а в параметрах указать, что модель линейная и переменные имеют неотрицательные значения. Поиск решения дает следующий результат: теневая цена на бетон - 40, на арматуру - 0, на труд - 60. Значение издержек равно 23 000 руб. и, заметим, оно в точности совпадает со значением прибыли в прямой задаче (рис.7,8).
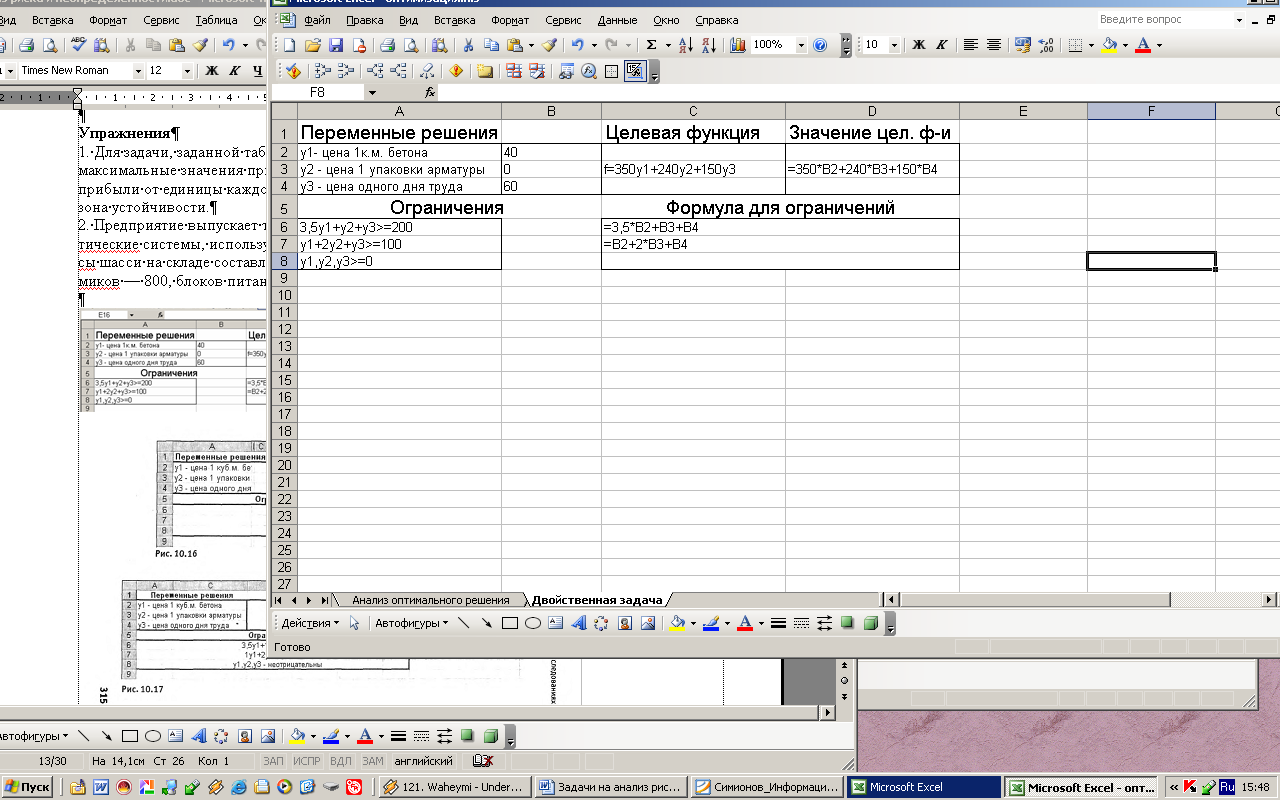
Рис.7
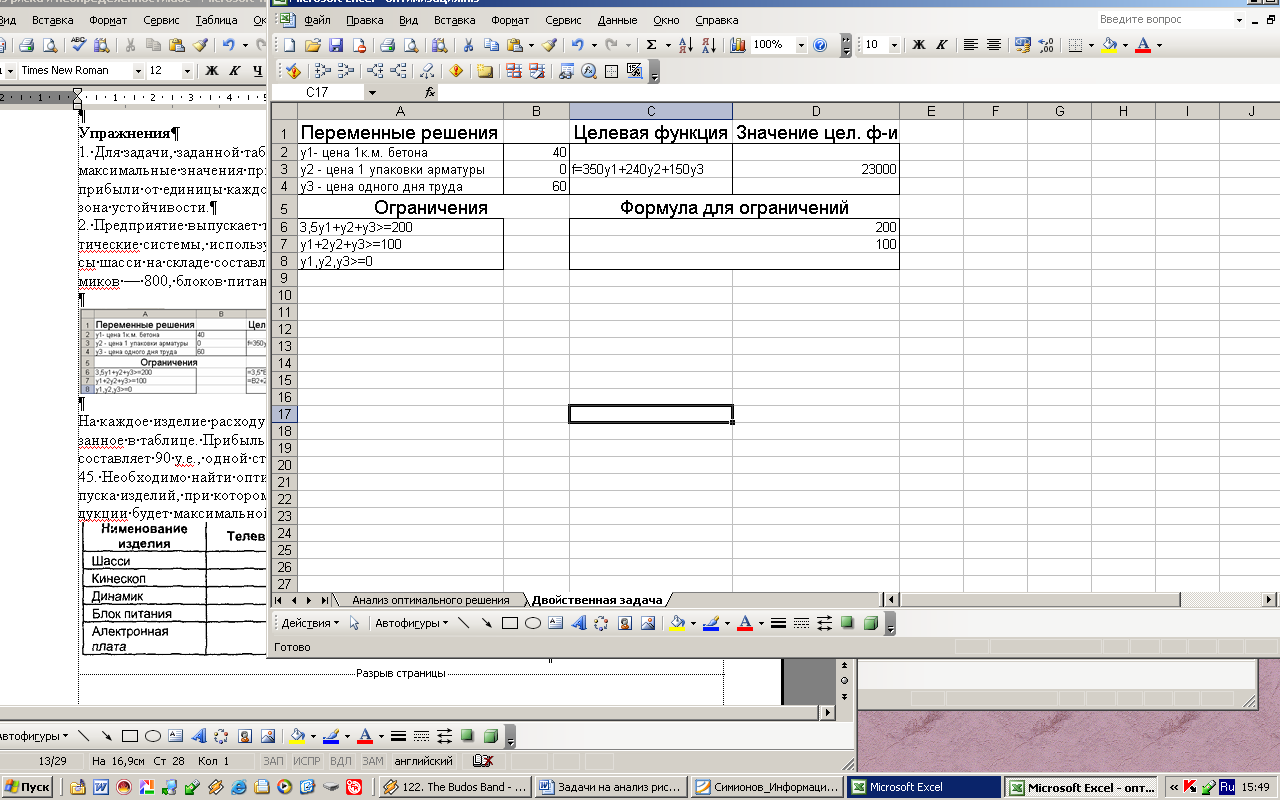
Рис.8
В теории линейного программирования доказано, что независимо от прикладной интерпретации, оптимальные значения целевых функций прямой и двойственной задач совпадают. Известно также, что теневая цена ресурса показывает, насколько увеличится прибыль от производства. Нулевая теневая цена на арматуру означает, что ресурс избыточен (рис.9).
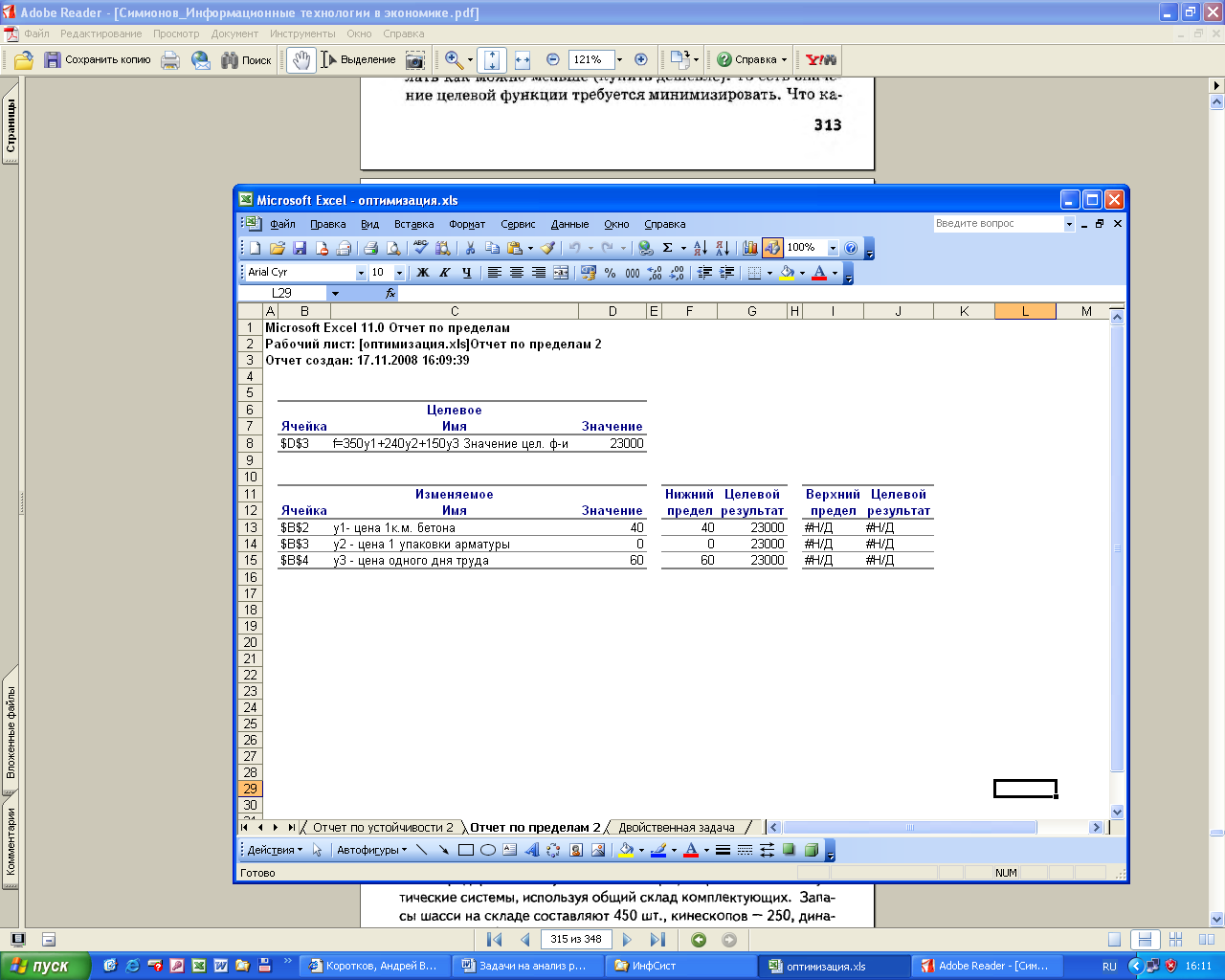
Рис.9
Упражнения для самостоятельной работы
1. Для задачи, заданной таблицей на рис.2, вычислить максимальные значения прибыли при увеличении и уменьшении прибыли от единицы каждого вида продукции в пределах диапазона устойчивости.
2. Предприятие выпускает телевизоры, стереосистемы и акустические системы, используя общий склад комплектующих. Запасы шасси на складе составляют 450 шт., кинескопов — 250, динамиков — 800, блоков питания — 450, плат — 600. На каждое изделие расходуется количество комплектующих, указанное в таблице. Прибыль от производства одного телевизора составляет 90 у.е., одной стереосистемы — 50 и аудиосистемы — 45. Необходимо найти оптимальное соотношение объемов выпуска изделий, при котором прибыль от производства всей продукции будет максимальной.
Ресурсы |
Запасы |
ТВ |
Стереосистема |
Акустическая система |
Шасси |
450 |
2 |
1 |
1 |
Кинескоп |
250 |
1 |
1 |
2 |
Динамик |
800 |
2 |
1 |
1 |
Блок питания |
450 |
5 |
1 |
1 |
Плата |
600 |
1 |
3 |
2 |