Задача о планировании производства

Постановка задачи. Предприятие должно производить изделия n видов: u₁ ,u₂,..,u_n, причем количество каждого выпускаемого изделия не должно превысить спрос и одновременно не должно быть меньше за планированных величин соответственно. На изготовление изделий идет m видов сырья , запасы которых ограничены соответственно величинами . Известно, что на изготовление i-го изделия идет a_ij единиц j —го сырья. Прибыль, получаемая от реализации изделий u₁ ,u₂,..,u_n, равна соответственно c₁, c₂,..,c_n. Требуется так спланировать производство изделий, чтобы прибыль была максимальной, и при этом выполнялся план на производство каждого изделия, но не превышался спрос на него.

Математическая модель. Обозначим за x₁ ,x₂,.., x_n, количества единиц изделий u₁ ,u₂,..,u_n выпускаемых предприятием. Прибыль, приносимая планом (целевая функция), будет равна:

z=z(x₁ ,x₂,.., x_n)=c₁x₁+ c₂x₂+ …+ c_nx_n max

Ограничение на выполнение плана запишется в виде: х_i b_i, для i = 1,2,...,п. Чтобы не превысить спрос, надо ограничить выпуск изделий: х_{i i}, для i = 1,2,...,п. И, наконец, ограничения на сырье запишутся в виде системы неравенств:

при условии, что x₁ ,x₂,.., x_n неотрицательны.

Рассмотрим конкретный пример задачи о планировании производства и приведем последовательность действий, необходимых для ее решения с помощью MS Excel.

Пример 1.

Предприятие выпускает два вида железобетонных изделий: лестничные марши и балконные плиты. Для производства одного лестничного марша требуется израсходовать 3,5 куб.м. бетона и 1 упаковку арматуры, а для производства плиты — 1 куб.м. бетона и 2 упаковки арматуры. На каждую единицу продукции приходится 1 человеко-день трудозатрат. Прибыль от продажи 1 лестничного марша составляет 200 руб., а одной плиты — 100 руб. На предприятии работает 150 человек, причем известно, что в день предприятие производит не более 350 куб.м. бетона и завозится не более 240 упаковок арматуры. Требуется составить такой производственный план, чтобы прибыль от производимой продукции была максимальной.

Решение.

1. На листе рабочей книги MS Excel заполните таблицу параметров задачи (рис.1).

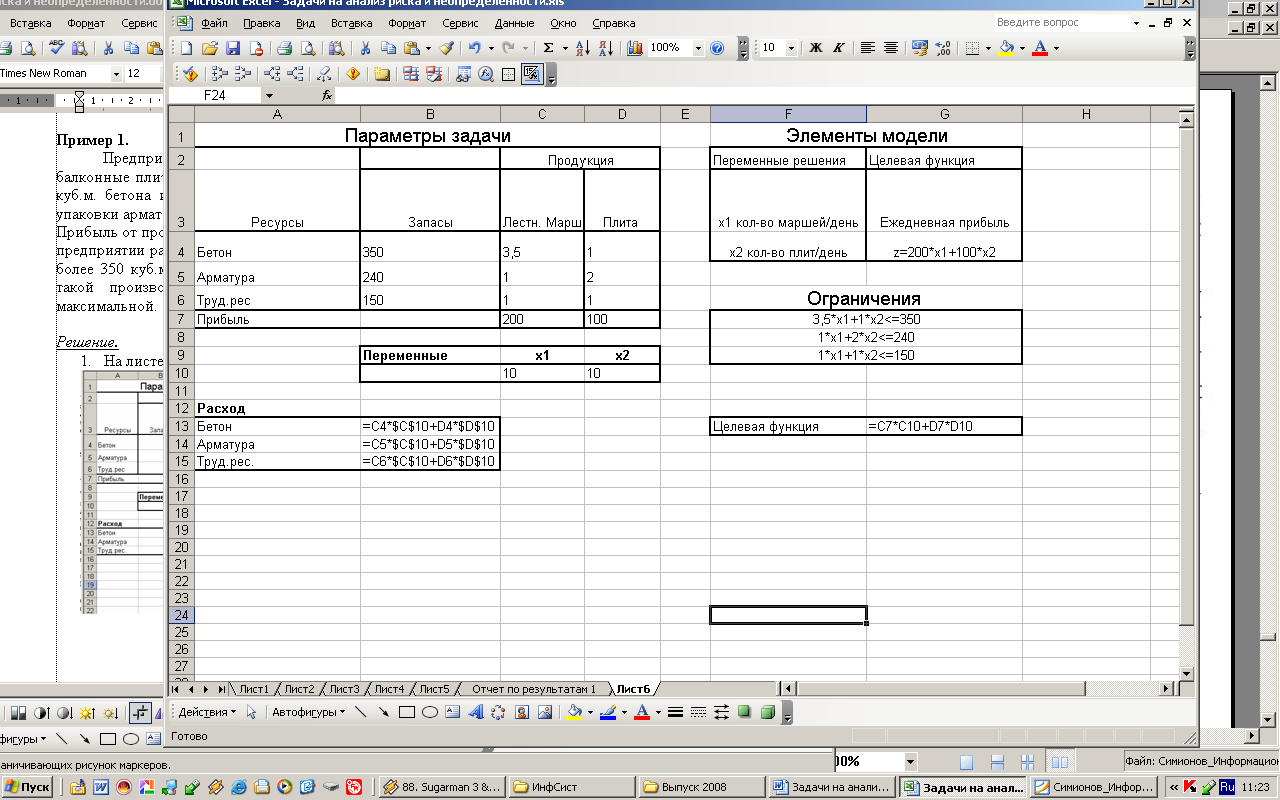
Рис.1

2. Создайте модель задачи и заполните ячейки для значений переменных (первоначально ячейки x1 и х2 заполняются произвольными числовыми значениями, например, значением 10), целевой функции (ячейка содержит формулу) и ограничений (ячейки содержат формулы) (рис.).

3. Выполните команду Сервис - Поиск решения и установите необходимые значения в полях диалогового окна Поиск решения, добавляя ограничения в окне Добавление ограничений.

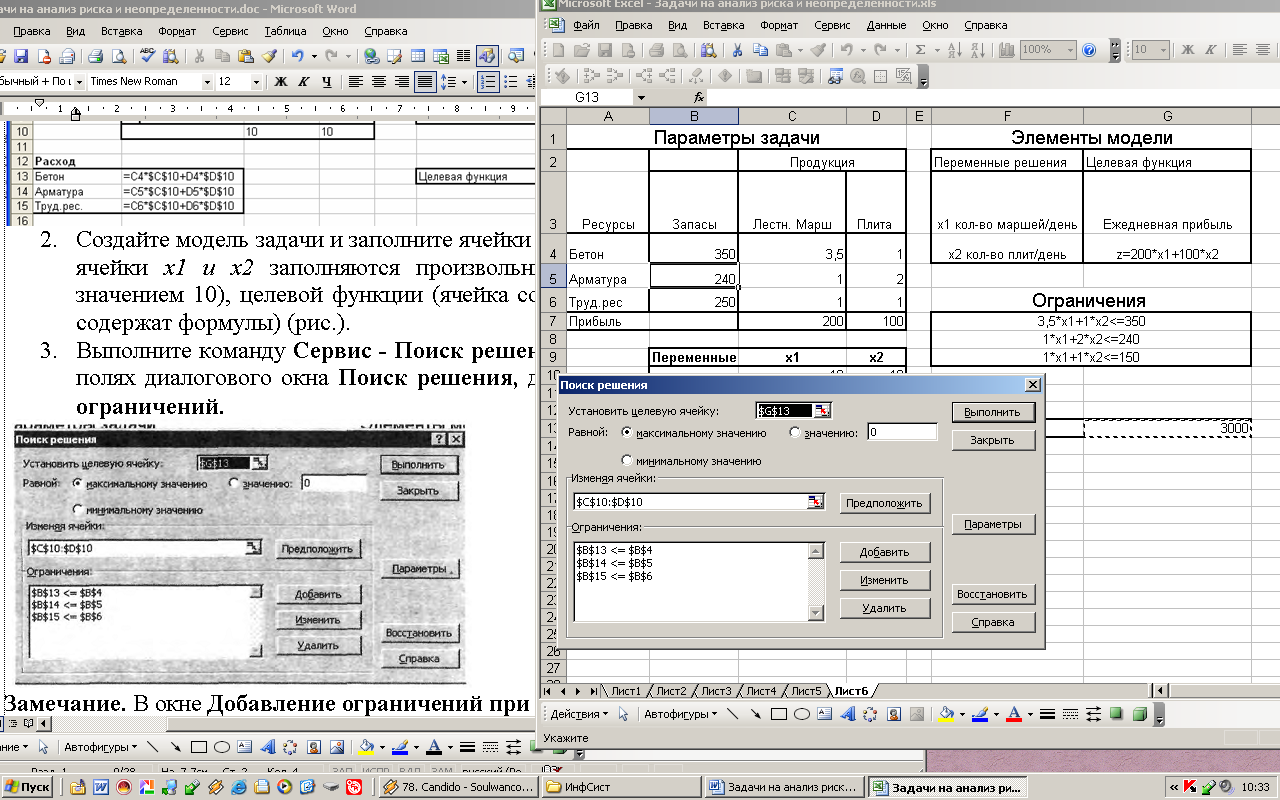
4. Нажмите на кнопку Выполнить и установите параметры в окне Результаты поиска решения (переключатель Сохранить найденное решение или Восстановить исходные значения и Тип отчета).

5. В результате в ячейках с переменными задачи появятся значения, соответствующие оптимальному плану (80 лестничных маршей и 70 плит перекрытия в день), а в ячейке для целевой функции — значение прибыли (23 000 руб.), соответствующее данному плану (рис.2).

Рис.2

6. В случае если полученное решение является удовлетворительным, можно сохранить оптимальный план и ознакомиться с результатами поиска, которые выводятся на отдельный лист (рис.3).

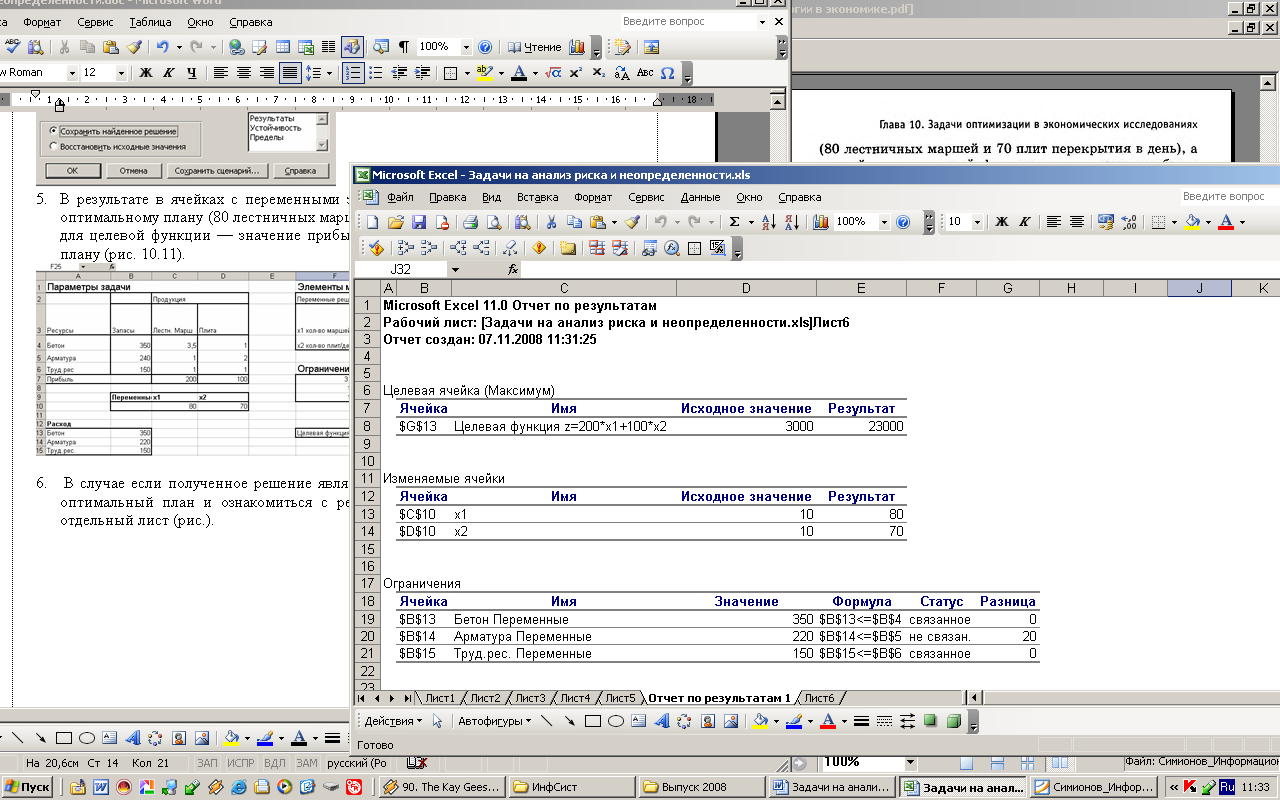
Рис.3