Задачи на анализ риска и неопределенности
Пример 1.
Продавец покупает журналы у издательства по 20 руб. за штуку, а продает по 21 руб. Если товар не продан, он возвращается издательству по 17 руб. Определить количество журналов, которые следует брать на реализацию, чтобы ожидаемая прибыль была максимальной. Предположим, что продавец выполнил статистический анализ своей деятельности за 37 рабочих дней.
Объем реализации |
0 |
5 |
10 |
15 |
20 |
25 |
Число событий (дней) |
0 |
7 |
9 |
15 |
6 |
0 |
Вероятность события |
0,00 |
0,19 |
0,24 |
0,41 |
0,16 |
0 |
Решение:
Пусть взято на реализацию n журналов (n {0,5,10,15,20}) при спросе m.
Прибыль от реализации составит:
Обозначим вероятность продажи m журналов Рm. Тогда ожидаемая прибыль:
Требуется найти такое n,
для которого
max.
Решение этой задачи иллюстрируется фрагментом файла Excel (см. рисунок).
В рассмотренном случае при решении задачи приняты два важных допущения.
1. Вероятности рассчитаны, исходя из наблюдений за 37 дней. Возможно, при увеличении срока наблюдений они изменятся.
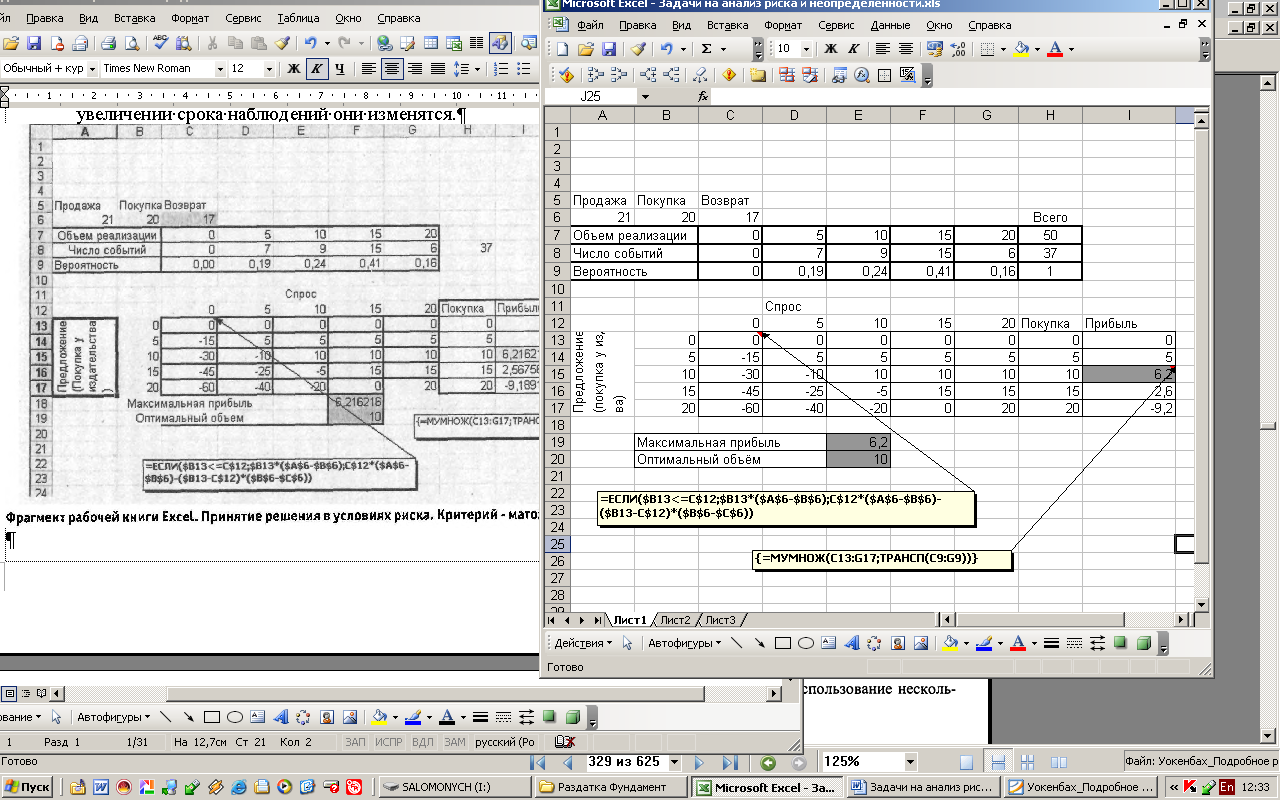
2. В качестве критерия принято ожидаемое значение целевой функции, т.е. математическое ожидание некоторой величины (в данном случае – прибыли).
Задачи оптимизации в экономических исследованиях
Пример 1.
Построить и исследовать динамику роста производства продукции, используя данные:
Год |
Производство |
1997 |
17,1 |
1998 |
18 |
1999 |
18,9 |
2000 |
19,7 |
2001 |
19,8 |
2002 |
19,9 |
Решение:
1. На основе имеющейся таблицы строим диаграмму Точечная. Наводим курсор на одну из точек полученного графика и из контекстного меню выбираем команду: Добавить линию тренда
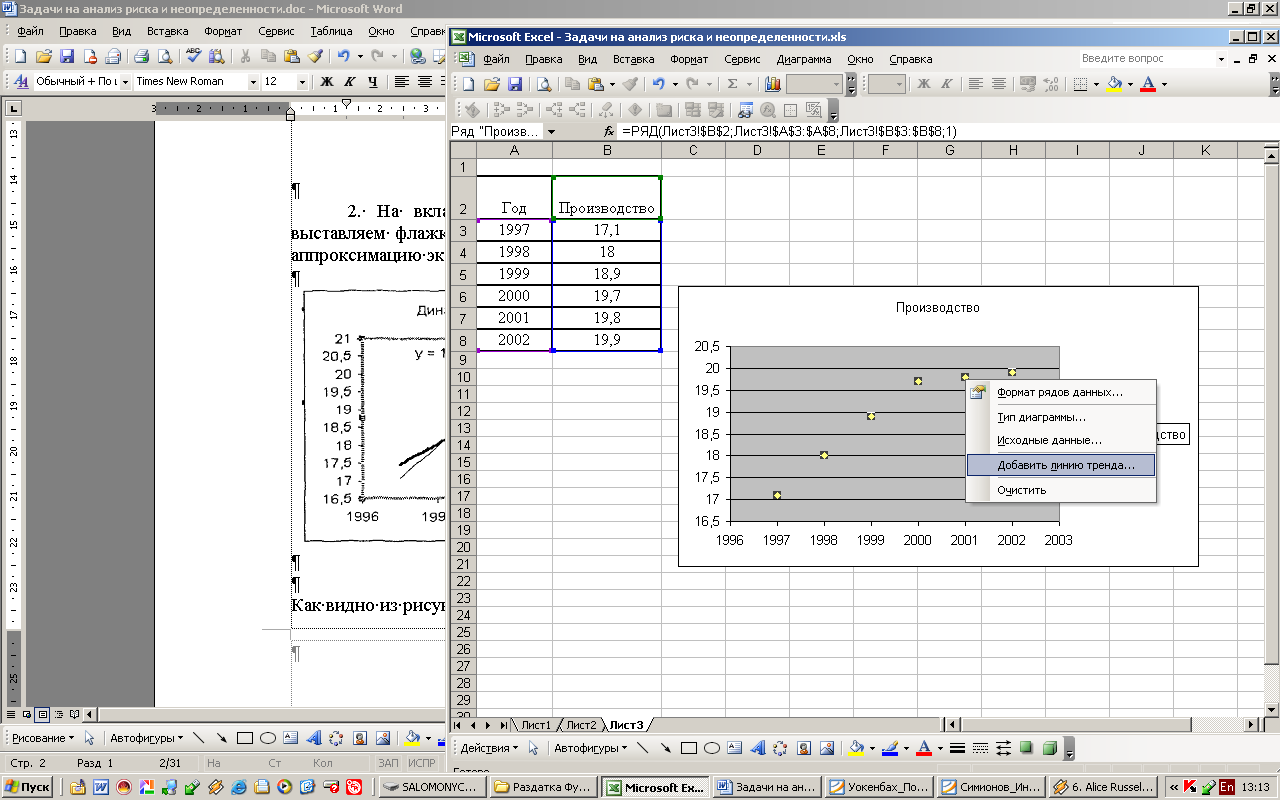
2. На вкладке Тип указываем тип Логарифмическая. На вкладке Параметры выставляем флажки для уравнения и достоверность аппроксимации В итоге мы получим аппроксимацию экспериментальных данных практически в виде прямой, показанной на рис.
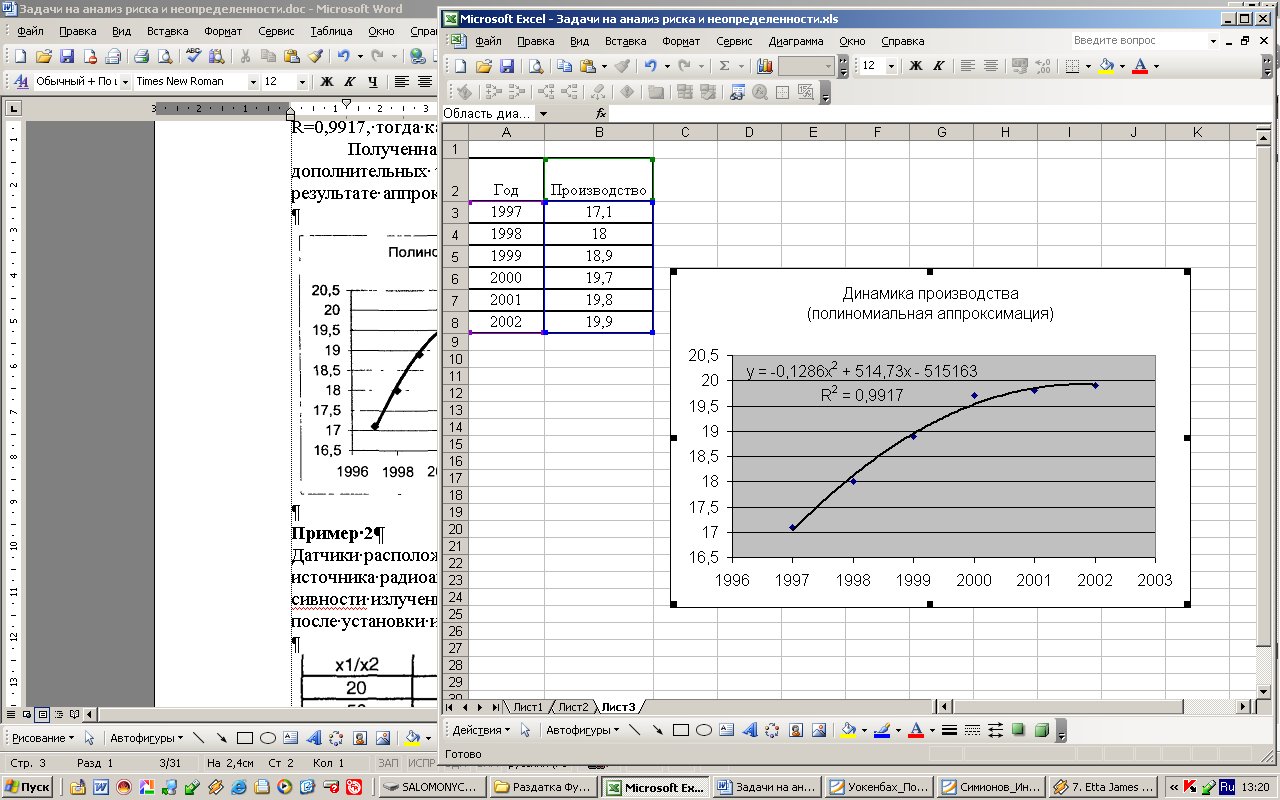
Как видно из рисунка, результат аппроксимации не является удовлетворительным. Для того, чтобы убедиться в правильности выбора типа аппроксимирующей функции, следует выбрать несколько разных функций для аппроксимации (трендов) и сравнить значения величин достоверности для каждого варианта тренда. Правая кнопка на линии тренда дает возможность редактировать его, подбирая другие функции для аппроксимации. Наилучшей в данном примере является полиномиальная функция, которая дает показатель достоверности R=0,9917, тогда как для логарифмической функции этот показатель равен 0,897 (см. рис.).
Полученная аналитическая зависимость позволяет вычислять значения функции в дополнительных точках. Для этого в ячейку листа MS Excel можно занести полученную в результате аппроксимации формулу со ссылкой на ячейку с независимой переменной.
Пример 2
Менеджерами книжного магазина в течение недели собирались данные о прибыли от продажи книг (у) в зависимости от числа посетителей магазина (x1) и числа покупок (х2). В результате была получена таблица:
x1 |
х2 |
Прибыль % |
120 |
20 |
32,5 |
100 |
25 |
28,3 |
130 |
20 |
33,7 |
100 |
15 |
33,1 |
110 |
23 |
30,5 |
105 |
26 |
39,1 |
112 |
16 |
38,4 |
Требуется построить эмпирическую таблицу, отражающую динамику прибыли в зависимости от числа посетителей (от 100 до 130) и числа покупок (от 15 до 25) с шагом 5.
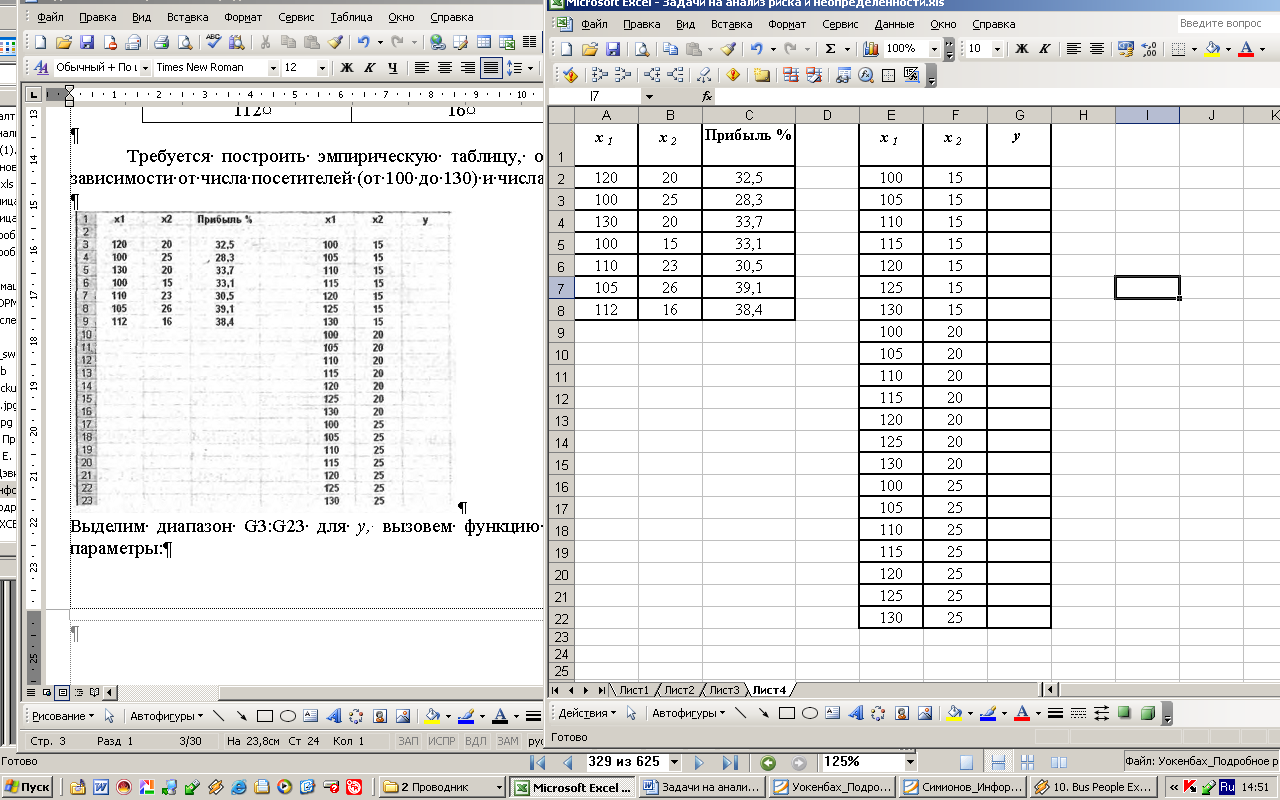
Выделим диапазон G3:G23 для у, вызовем функцию ТЕНДЕНЦИЯ и укажем для нее параметры:
Нажмем сочетание клавиш CTRL+SHIFT+ENTER и получим результат в столбце у:
Упражнения для самостоятельной работы
Построить функции, наилучшим образом аппроксимирующие зависимости:
x |
1,0 |
1,5 |
3,0 |
4,5 |
5,5 |
Y |
1,25 |
1,4 |
1,5 |
1,75 |
2,25 |
Построить функцию, отражающую зависимость дефицита бюджета от времени в России и США.
Страна |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
Россия |
2,9 |
2,3 |
3,1 |
2,2 |
2,0 |
2,7 |
6,5 |
8,0 |
9,1 |
США |
2,8 |
2,6 |
4,1 |
6,3 |
5,0 |
5,4 |
5,3 |
3,4 |
3,2 |
Вложенные в производства средства дают прибыль:
Средства |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
Прибыль |
850 |
900 |
1000 |
1300 |
2000 |
4000 |
Определить зависимость прибыли от вложенных средств и вычислить прибыль для вложений, равных 10 000 руб.