
Рассмотрим теорию теплоемкости идеального газа.
Величина теплоемкости, характеризующая свойства газов, не является для данного газа величиной постоянной, а зависит от условий, при которых происходит нагревание. Эту зависимость можно получить, воспользовавшись первым началом термодинамики.
1-й закон — первое начало термодинамики: Представляет собой формулировку обобщённого закона сохранения энергии для термодинамических процессов. В наиболее простой форме его можно записать как
dQ=dU+dA = dU + PdV, (4)_
где dU есть полный дифференциал внутренней энергии системы, а dQ есть элементарное количество теплоты, переданное системе, а dA элементарная работа, совершенная системой против внешних сил. Нужно учитывать, что dA и dQ нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.
Если нагревание газа происходит при постоянном объёме, то газ не совершает работы (PdV=0) и, следовательно, согласно первому началу термодинамики, все количество теплоты идет на увеличение внутренней энергии газа:
dQ=dU (5)
Внутренняя энергия одного моля идеального газа U = i/2*RT, (6)
Где i – число степеней свободы молекулы газа, R – универсальная газовая постоянная.
Число степеней свободы — это число независимых переменных, полностью определяющих положение молекулы как системы атомов в пространстве.
Теплоемкость одного киломоля идеального газа при постоянном объёме
CV = dQ/dT = dU/dT= i/2*R (7)
Частные случаи первого закона термодинамики для изопроцессов:
Изохорический или изохорный процесс (от др.-греч. ἴσος «равный» и χώρος «место») — термодинамический процесс, который происходит при постоянном объёме.
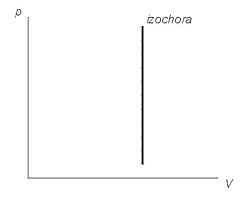
Т.К.при изохорном процессе объем газа остается постоянным, поэтому газ не совершает работу. Изменение внутренней энергии газа происходит благодаря теплообмену с окружающими телами:
Q = dU
Изобарный процесс (др.-греч. ἴσος «одинаковый» и βάρος «тяжесть») — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа.
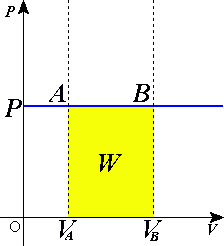
При изобарном расширении газа подведенное к нему количество теплоты расходуется как на увеличение его внутренней энергии и на совершение работы газом:
Q = dU + PdV (8)
Из уравнения Клайперона
PV = RT (9)
Следует
PdV = RdT (!0)
и
dQ =dU + RdT, (11)
отсюда молярная теплоемкость при постоянном давлении
Cp = dQ/dT = dU/dT = R , (12)
Следовательно, исходя из формулы (7) где CV = dU/dT – молярная теплоемкость при постоянном объёме. Следовательно
CP = CV + R (13)
Это – уравнение Майера, связывающее теплоемкости изобарного и изохорного процессов: молярная теплоемкость идеального газа при постоянном давлении больше молярной теплоемкости при постоянном объёме на величину универсальной постоянной R
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством
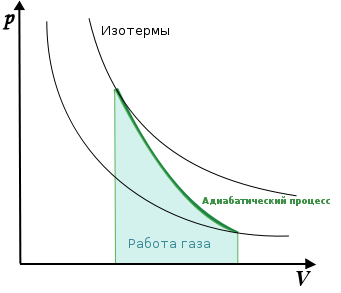
При таком процессе уравнение (4) примет вид
dU + dA = 0
или dA = - dU (14)
т.е при адиабатическом расширении или сжатии работа совершается газом только за счет изменения запаса внутренней энергии. Уравнение адиабатического процесса (уравнение Пуассона) может быть выведено следующим образом. Поскольку dA = PdV, а dU = CVdT, то уравнение (14) принимает вид:
PdV = - CVdT (15)
Разделив это уравнение на (9), получим
dV/V = -CV/R * dT/T
или R/CV *dV/V +dT/T = 0 (16)
Учитывая уравнение Майера , получим выражение для множителя
R/CV= (CP-CV)/CV = СP/CV – 1.
Если обозначить CP/CV = γ, то уравнение (16) примет вид
(γ – 1) dV/V + dT/T = 0 (17)
Интегрируя и потенцируя уравнение (17), находим
In VY-1 + In T = const,
T * VY-1 = const. (18)
Величина γ зависит только от числа степеней свободы молекул, из которых состоит газ.
Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.
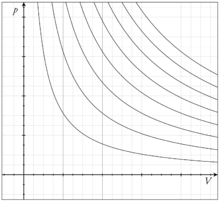
При изотермическом процессе количество теплоты, переданное газу от нагревателя, полностью расходуется на совершение работы:
Q = dA
