Вариант 19.

1. Для определения оценок параметров линейной модели множественной регрессии путем минимизации суммы квадратов отклонений фактических значений от расчетных применяется:

а) метод наименьших квадратов;

б) метод максимального правдоподобия;

в) метод Монте-Карло;

г) метод моментов.

2. Какая запись модели множественной регрессии является неверной:

а)

б) ;

в) ;

г) .

3. Получена следующая модель пространственной выборки:

Y = 123,35 + 0,53X₁ - 9,89X₂ + ε.

Как интерпретируется коэффициент при факторном признаке X₂:

а) при увеличении фактора X₂ на 1% результативный признак в среднем будет увеличиваться на 9,89%;

б) при увеличении только фактора X₂ на 1% результативный признак в среднем будет уменьшаться на 9,89%;

в) при увеличении только фактора X₂ на 1 единицу измерения результативный признак будет в среднем уменьшаться на 9,89 своих единиц измерения;

г) при увеличении только фактора X₂ на 1 единицу измерения результативный признак будет уменьшаться на 9,89 своих единиц измерения.

4. Для уравнения регрессии с двумя факторными признаками значения R²  и 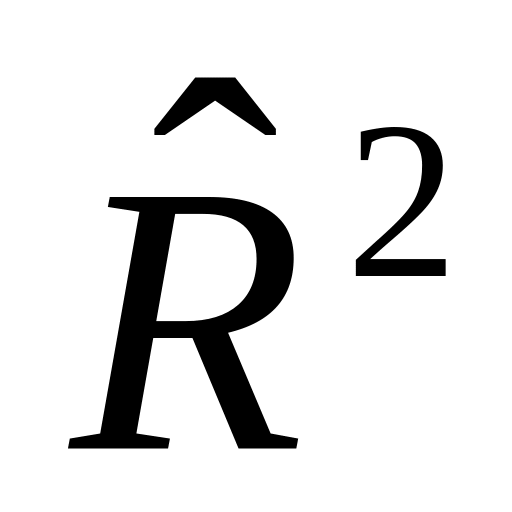составили соответственно 0,9878 и 0,9763. При добавлении в уравнение третьего фактора получили, что R² =0,9882 и =0,9752. О чём говорит этот факт?

а) при расчете R²  и во второй раз была допущена ошибка, так как не может уменьшаться при добавлении нового фактора;

б) третий фактор оказался несущественным и его включение в модель нецелесообразно;

в) этот факт ничего не значит; им можно пренебречь.

5. При проверке модели множественной регрессии y=f(x₁,x₂,x₃) + ε на наличие автокорреляции с помощью теста Дарбина-Уотсона было получено следующее значение d=1,79. При уровне значимости α=0,05 и числе наблюдений n=24 табличные значения составляют d_н=1,10 и d_в=1,66 . Какой вывод можно сделать по результатам теста:

а) гипотеза об отсутствии автокорреляции не отвергается (принимается);

б) вопрос об отвержении или принятии гипотезы остается открытым, так как расчетное значение попадает в зону неопределенности;

в) принимается альтернативная гипотеза о наличии положительной автокорреляции;

г) принимается альтернативная гипотеза о наличии отрицательной автокорреляции;

6. При исследовании зависимости объема потребления продукта А (y) от времени года были введены следующие фиктивные переменные: d₁ (1 - если месяц зимний, 0 – в остальных случаях), d₂ (1 - если месяц весенний, 0 – в остальных случаях), d₃ (1 - если месяц летний, 0 – в остальных случаях) и получено следующее уравнение Y = b₀ + b₁d₁ + b₂d₂ + b₃d₃+ ε.

Чему равна разница среднемесячного объема потребления между весенними и осенними месяцами:

а) b₀;

б) b₂;

в) b₀ – b₂;

г) b₀ + b₂.

7. В производственной функции Кобба-Дугласа Y = AK^αL^β ε параметр  α соответствует коэффициенту:

а) корреляции;

б) детерминации;

в) эластичности;

г) автокорреляции.

8. Чему равен параметр авторегрессии в модели вида y_t = -0,71y_t-1 + ε_t:

а) 0,71;

б) 0,71²;

в) -0,71;

г) (-0,71)².

9. Изучается зависимость объема ВВП (Y, млрд. долл.) от уровня прибыли в экономике (Х_t, млрд. долл.). Получена следующая модель с распределенным лагом:

Y_t = 0,65∙X_t + 0,30∙X_t-1 + 0,10∙X_t-2 + 0,05∙X_t-3 + ε_t.

Чему равен краткосрочный мультипликатор:

а) 0,05;

б) 0,65;

в) 0,30;

г) 0,95.

10. Структурная форма модели имеет вид:

где: Ct – совокупное потребление в период t, Yt – совокупный доход в период t, It – инвестиции в период t, Тt – налоги в период t, Gt – государственные расходы в период t, Yt-1 – совокупный доход в период t-1.

Сколько предопределенных переменных в данной системе:

а) 2;

б) 3;

в) 4;

г) 5.