5.2. Расчет магнитной цепи методом участков[1].

Задача состоит в том, чтобы по известному потоку Фδ определить МДС обмотки. Расчет проводится методом последовательных приближеий задаваясь удельной МДС.

Алгоритм расчета:

1) Задаемся удельной МДС:

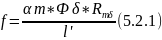
αm – коэффициент, учитывающий падение магнитного напряжения на магнитопроводе (при первом приближении принимаем равным 1,1); l’ – длина магнитопровода, вдоль которого распределена МДС; l’ = l-C_lll-l₂. Так как l₂ много меньше l и C_lll , то этой длиной можно пренебречь, тогда:

l’ = l – C_lll (5.2.2)

2) Найдем магнитную индукцию в зазоре:

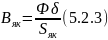
– площадь поперечного сечения якоря.

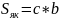(5.2.4)

Воспользуемся кривой намагничивания стали 1211 (см. Приложение 1.)

Находим напряженность магнитного поля: для этого воспользуемся кривой намагничивания стали 1211 (см. Приложение 1. Рис. 5.) и в дальнейшем при поиске Н тоже будем пользоваться этой кривой.

Зная В_як и Н_як , находим магнитную проницаемость якоря:

Находим магнитное сопротивление якоря

l_як – длина средней линии пути прохождения потока в якоре.

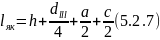
3) Найдем магнитное напряжение между узлами 1 и 1’ магнитной цепи (см. рис. 3. 2).

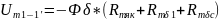(5.2.8)

4) Зная магнитное напряжение между точками 1 и 1’ и сопротивление , найдем поток рассеяния

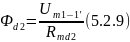
5) Найдем магнитный поток между узлами 1 и 2; 2’ и 1’:

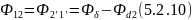
6) Найдем магнитную индукцию на участке 1 – 2 и 2’ – 1’

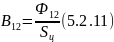
– площадь поперечного сечения половины центрального стержня

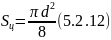
Зная 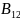, найдем напряженность 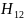и получим магнитную проницаемость:

Аналогично для участка 2’ – 1’

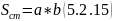
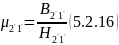
7) Найдем магнитные сопротивления участков 1 – 2 и 2’ – 1’

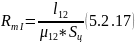
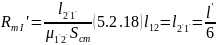
Далее длины участков 1 – 2, 2’ – 1’, 4 – 6 и 5’ – 4’ будем обозначать 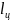, а длины участков 2 -3, 3 – 4, 3’ – 2’, 4’ – 3’ будут в 2 раза больше, будем обозначать их :

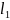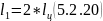
8) Найдем магнитные напряжения между узлами 2 и 2’

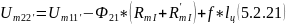
9) Найдем поток рассеяния

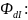
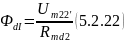
Тогда поток между узлами 2 – 3 и 3’ – 2’

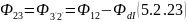
10) Найдем магнитную индукцию для участка магнитопровода 2 – 3 и 3’ – 2’

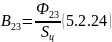
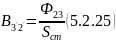
Находим 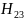и 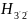и расчитываем магнитную проницаемость

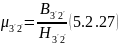
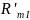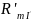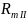11) Найдем магнитные сопротивления и , и

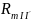
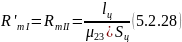
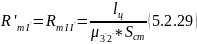
12) Найдем магнитное напряжение между узлами 3 и 3’ магнитной цепи

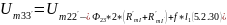
Удвоенное сопротивление магнитопровода берем, т.к. ,

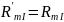13) Найдем поток рассеяния 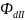участка II

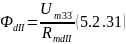
Поток между узлами 3 и 4, 4’ и 3’

14) Найдем магнитную индукцию для участка магнитопровода 3 – 4 и 4’ – 3’

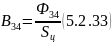
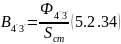
Находим магнитные напряженности 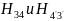соответствующие 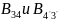и расчитываем магнитную проницаемость

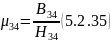
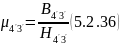
15) Найдем магнитные сопротивления участка магнитопровода 3 - 4

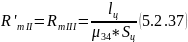
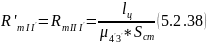
16) Найдем магнитное напряжение между узлами 4 и 4’ магнитной цепи:

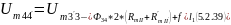
17) Найдем поток рассеяния 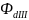участка III

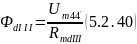
18) Поток между узлами 4 и 5, 5’ и 4’

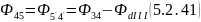
19) Найдем магнитную индукцию :

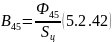
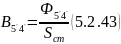
Находим магнитные напряженности 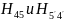соответствующие 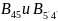и расчитываем магнитную проницаемость

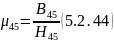
20) Найдем магнитные сопротивления участков 4 – 5 и 5’ – 4’ :

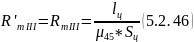
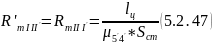
21) Магнитный поток в ярме будет равен магнитному потоку на участке 4 - 5 магнитной цепи:

22) Найдем магнитную индукцию в ярме:

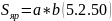
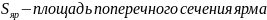
Зная магнитную индукцию в ярме, по кривой намагничивания стали найдем магнитную напряженность поля в ярме 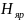и рассчитаем

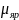
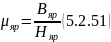
23) Магнитное сопротивление ярма

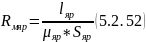
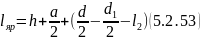
24) Теперь найдем магнитные напряжения между бесконечно близкими точками 6 и 6’

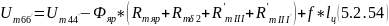
Напряжение 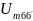должно быть равно нулю, т.к. точки 6 и 6’ бесконечно близки. Следовательно, если в результате этого расчета < 0, то в самом начале надо увеличить удельную МДС, для этого надо увеличить коэффициент αm, если в результате > 0, то в самом начале надо уменьшить удельную МДС, для этого надо уменьшить коэффициент αm и повторить расчет.