1.8 Определение запаса устойчивости по фазе на лчх

Критерий устойчивости, основанный на логарифмических частотных характеристиках разомкнутой системы, это основной метод анализа и синтеза динамических систем, позволяющий оценить устойчивость замкнутой системы по поведению её в разомкнутом состоянии.

Если ЛАЧХ пересекает ось частот раньше, чем фазовая характеристика, то такая система устойчива.

Используя вычислительную среду SamSim приведем графики ЛАЧХ и ЛФЧХ исходной и скорректированной систем, соответствующих различным коэффициентам разомкнутой системы.

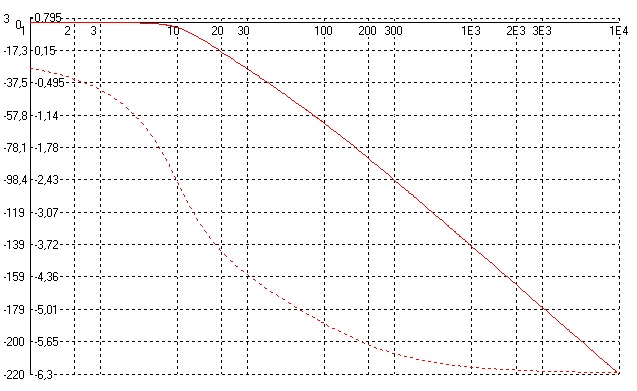
Рисунок 12 – Графики ЛАЧХ и ЛФЧХ

Как видно из графиков системы являются устойчивыми. Запас устойчивости по фазе Δφ=40º.

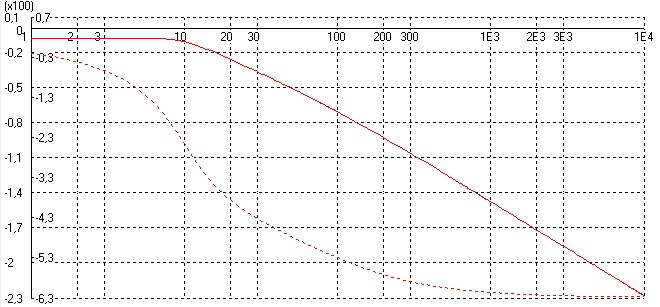
Рисунок 13 – Графики ЛАЧХ и ЛФЧХ при уменьшении коэффициента усиления

Как видно из графиков система является устойчивой. Значит устойчивость по фазе Δφ=50 %.

Таким образом, можно сделать вывод, что изменяя коэффициент усиления можно влиять на запас устойчивости по фазе. При увеличении коэффициента усиления устойчивость по фазе падает, а при уменьшении запас устойчивости по фазе растет.

1.9 Коррекция сау за счет введения последовательного корректирующего устройства

Для выполнения требований по устойчивости, точности и качеству переходных процессов применяют коррекцию динамических свойств САУ. Коррекция используется для обеспечения устойчивости неустойчивой САУ, расширения запасов и области устойчивости, повышения качественных показателей переходных процессов. Коррекция осуществляется с помощью введения в систему корректирующих звеньев с определенной передаточной функцией.

Используя вычислительную среду SamSim, рассмотрим две структурные схемы неустойчивых автоматических систем и скорректируем САУ за счет введения последовательного корректирующего устройства.

Рисунок 14 – Структурная схема первой системы

Рисунок 15 – Структурная схема второй системы

Исходные данные:

k₁=1 k₃=1

T₁=0,1 T₂=0,4

k₂=1 C=0,25

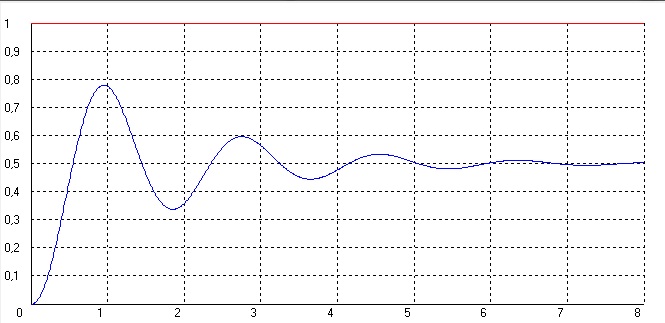
Рисунок 16 – График первой системы без корректирующего звена

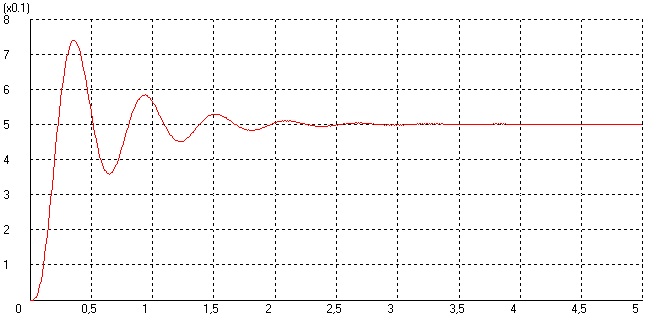
Рисунок 17 – График второй системы без корректирующего звена

Теперь представим структурные схемы с корректирующими звеньями:

Рисунок 17 – Структурная схема первой системы с корректирующим устройством

Рисунок 18 – Структурная схема первой системы с корректирующим устройством

Меняя коэффициент устойчивости К₄ можно добиться устойчивости системы.

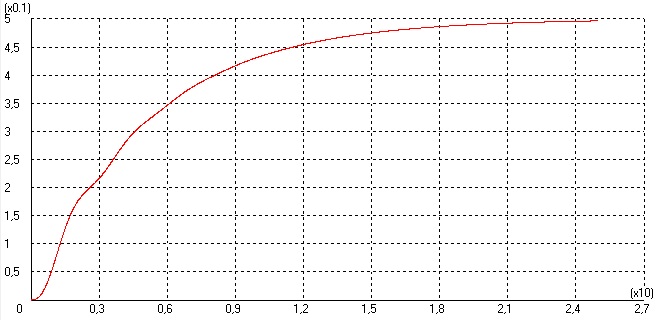
Рисунок 19 – График первой системы с корректирующим элементом

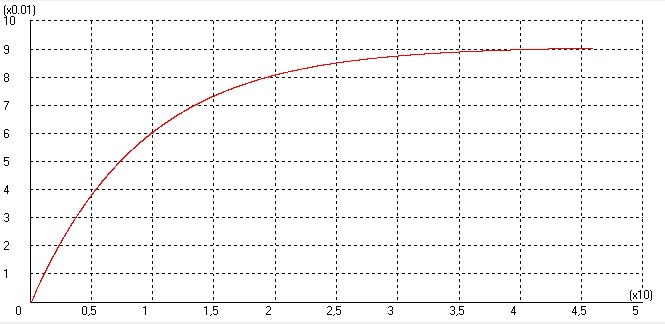
Рисунок 20 – График второй системы с корректирующим элементом

2 Исследование нелинейной системы автоматического управления

2.1 Анализ нелинейной системы автоматического управления

К нелинейным системам относятся системы, в которых связь между выходной и входной величинами одного или нескольких элементов задается нелинейными дифференциальными уравнениями. Примером существований нелинейности, которой никогда нельзя пренебречь, является релейная характеристика. Включение в систему звена с такой характеристикой придает системе качественно новые свойства.

Используя возможности вычислительной среды SamSim, проанализируем нелинейную систему автоматического управления соответствующей структурной схеме:

Рисунок 21 – Структурная схема системы

Исходные данные:

К₁=10 К₃=1

Т₁=1 Т₂=0,01

К₂=5 С=1

Т₃=8

При рассмотрении устойчивости таких систем необходимо оговаривать начальные условия и внешние воздействия. В связи с этим при изучении нелинейных систем употребляются понятия устойчивости в малом, в большом и в целом.

Устойчивость в малом – это устойчивость при бесконечно малых отклонениях от исходного режима. Устойчивость в большом – это устойчивость при конечных отклонениях, допустимых по условию работы системы. Устойчивость в целом – это устойчивость при неограниченных отклонениях.

Рассмотрим полученный фазовый портрет при нахождении в структурной схеме идеального двухпозиционного реле:

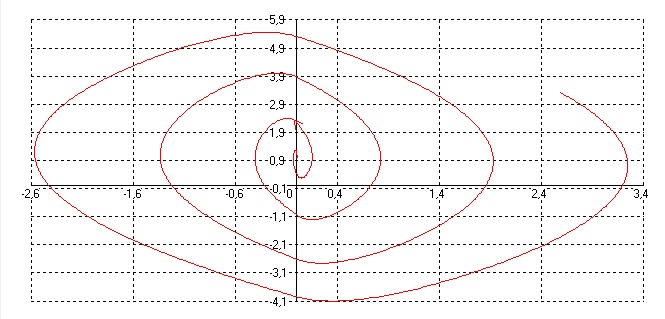
Рисунок 22 – Фазовый портрет с идеальным двухпозиционным реле

Для данного фазового портрета вводились начальные условия X₀(0)=1;

T_k=1с. Как видно из фазового портрета система неустойчива в малом до того момента, пока не достигнет предельного цикла.

Рисунок 23 – Фазовый портрет с идеальным двухпозиционным реле

Для данного фазового портрета вводились начальные условия X₀(0)=20; T_k=8с. Как видно из фазового портрета система неустойчива в большом до того момента, пока не достигнет предельного цикла.

Теперь заменим в структурной схеме идеальное двухпозиционное реле на двухпозиционное реле с зоной нечувствительности.

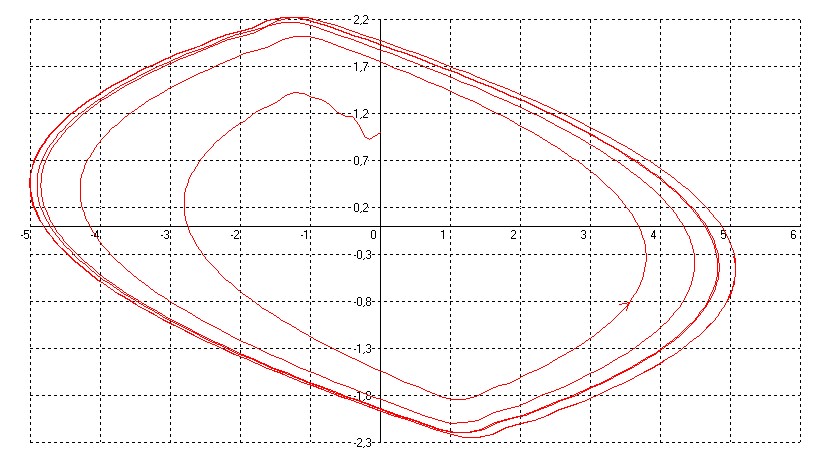
Рисунок 24 – Фазовый портрет с двухпозиционным реле с зоной нечувствительности

Для данного фазового портрета вводились начальные условия X₀(0)=1; T_k=1с. Как видно из фазового портрета система неустойчива в малом до того момента, пока не достигнет предельного цикла.

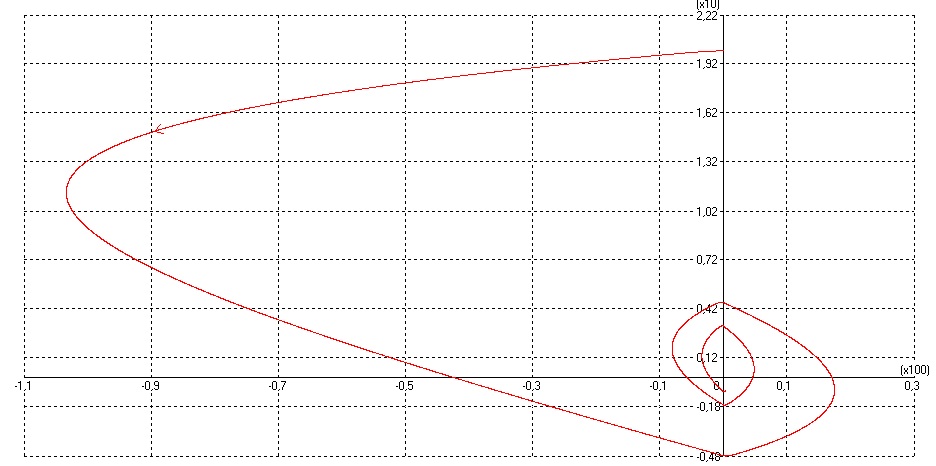
Рисунок 25 – Фазовый портрет с двухпозиционным реле с зоной нечувствительности

Для данного фазового портрета вводились начальные условия X₀(0)=20; T_k=8с. Как видно из фазового портрета система неустойчива в большим до того момента, пока не достигнет предельного цикла.