Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА (национальный исследовательский университет)»
(СГАУ)
Факультет летательных аппаратов
Кафедра летательных аппаратов
Расчетно-графическя работа по курсу
«Теория автоматического управления»
Вариант № 17
Выполнила студент группы 1308 Николаева О.В.
Проверил доцент Давыдов Е.И.
Самара 2012
Введение
В данной расчетной работе представлены исследования линейной и нелинейной систем автоматического управления. Построена математическая модель линейной системы автоматического управления, которая представлена в виде передаточной функции. Для данной автоматической системы построены частотные характеристики и проведено исследование на устойчивость. Для нелинейной системы автоматического управления проведен анализ и коррекция за счет корректирующего устройства.
Целью работы служит исследование линейных систем автоматического управления и анализ нелинейных систем автоматического управления.
Содержание
Введение 2
1.Исследование линейных систем автоматического управления 4
1.1 Структурная схема автоматической системы с численными значениями коэффициентов 4
1.2Преобразование исходной системы к одноконтурной и определение передаточной функции разомкнутой систем 5
1.3 Нахождение характеристического полинома замкнутой системы 6
1.4 Определение устойчивости системы по алгебраическому критерию устойчивости Гурвица 7
1.5 Определение устойчивости замкнутой системы по частному критерию Михайлова 8
1.6 Определение устойчивости системы по частотному критерию Найквиста 10
1.7 Влияние коэффициента усиления разомкнутой системы на устойчивость 13
1.8 Определение запаса устойчивости по фазе на ЛЧХ 17
1.9 Коррекция САУ за счет введения последовательного корректирующего устройства 19
2 Исследование нелинейной системы автоматического управления 23
2.1 Анализ нелинейной системы автоматического управления 23
Заключение 28
Список используемых источников 29
1.Исследование линейных систем автоматического управления
1 .1 Структурная схема автоматической системы с численными значениями коэффициентов
Рисунок 1 – Структурная схема автоматической системы
Исходные данные:
k1=1 T2=0,32
T4=0,1 T5=0,4
k4=3 k5=2,25
C5=0,25
W1(p)=k1 – усилительное звено;
W2(p)=T2*p – дифференцирующее звено;
W3(p)=k3 - усилительное звено;
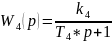- апериодическое звено 1-ого порядка;
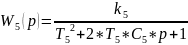- колебательное звено.
Вычислим численное значение звеньев:
W1(p)=k1=1;
W2(p)=T2*p=0,35p;
W3(p)=k3=1;
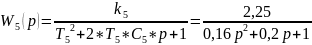
1 .2Преобразование исходной системы к одноконтурной и определение передаточной функции разомкнутой систем
Рисунок 2 – Структурная схема автоматической системы
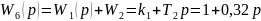
Рисунок 3 – Структурная схема автоматической системы
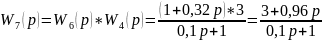
Рисунок 4 – Одноконтурная структурная схема автоматической системы
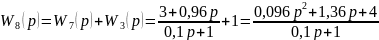
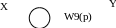
Рисунок 4 – Одноконтурная структурная схема автоматической системы
Исходя из полученной передаточной функции разомкнутой системы получим передаточную функцию замкнутой системы.
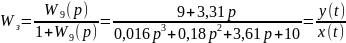
1.3 Нахождение характеристического полинома замкнутой системы
Общий вид характеристического уравнения замкнутой системы:
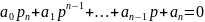
Из полученной передаточной функции замкнутой системы можно выделить характеристическое уравнение замкнутой системы. Этим уравнением будет являться знаменатель функции:
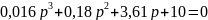
1.4 Определение устойчивости системы по алгебраическому критерию устойчивости Гурвица
В соответствии с критерием Гурвица составляется таблица:
a1 a3 a3 0
a0 a2 a3 0
0 a1 a3 0
0 0 0 an
Для устойчивости замкнутой системы (вещественная часть корней будет отрицательной) необходимо и достаточно, чтобы при а0 > 0 все диагональные определители таблицы, составленной по определенному правилу были больше нуля:
а0 >0, Δi >0.
Выпишем значения коэффициентов, из которых состоит таблица Гурвица, из характеристического уравнения.
а0=0,016;
а1=0,18;
а2=3,61;
а3=10.
Составим таблицу Гурвица:
a1 a3 0
a0 a2 0
0 a1 a3
Находим диагональные определители таблицы:
Δ1=а1 >0;
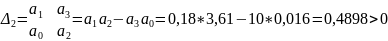
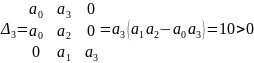
Таким образом, исходя из того, что все диагональные определители больше нуля и все коэффициенты аi больше нуля, можно сделать вывод, что данная замкнутая система устойчива.