
- •(Подпись, дата)
- •Харьков 2012 содержание
- •1 Структурный анализ
- •2 Исследование кинематики механизма аналитическим методом. Метод замкнутых контуров
- •3 Исследование кинематики механизма векторно-графическим методом. Метод планов скоростей и ускорений
- •4 Сравнение результатов двух методов
- •Планы положения, скоростей и ускорений механизма листинг программы
- •Протокол работы программы
4 Сравнение результатов двух методов
Погрешность в процентах результата, полученного векторно-графическим методом, определяем по формуле
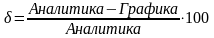 .
(4.1)
.
(4.1)
В табл.4.1 приведены результаты сравнения.
Таблица 4.1
Величина |
Аналитический |
Графический |
Погрешность, % |
|
1340.4129 |
1340.4129 |
0 |
|
1160.8316 |
1160.7975 |
0.0029334 |
. рад/с |
8.3776 |
8.3776 |
0 |
|
38899.8401 |
38898.699 |
0.0029334 |
|
39302.958 |
39302.958 |
-1.8512e-014 |
. рад/с2 |
0 |
0 |
0 |
ВЫВОДЫ
Аналитический метод позволяет построить математическую модель кинематики механизма. В качестве входных параметров этой модели приняты:
- закон движения ведущего звена;
- размеры звеньев;
- координаты некоторых точек, например, координаты шарнира ползуна.
Выходными параметрами этой модели являются временные зависимости кинематических величин, характеризующих движение механизма. Получение этих зависимостей позволяет проводить различные исследования движения механизма.
Трудность применения аналитического метода обусловлена способом решения разрешающей системы уравнений. Но при наличие соответствующего программного обеспечения эта трудность несущественна.
Векторно-графический метод позволяет получить решение только для одного положения механизма. В этом состоит его основной недостаток.
Простота и наглядность получения решения являются преимуществами векторно-графического метода. При применении соответствующих программ автоматизированного проектирования точность решения, получаемого данным методом, вполне достаточная.
Сравнение результатов, полученных двумя методами кинематического исследования, показало “почти” их совпадение. В первую очередь это связано с тем, что планы скоростей и ускорений нами строились программой КОМПАС.
Планы положения, скоростей и ускорений механизма листинг программы
clc,clear
%
% КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПРИБОРНЫХ МЕХАНИЗМОВ
%
% ИСХОДНЫЕ ДАННЫЕ
%
% Номер кинематической схемы ........................................
N_shema=5;
% Вариант данных ....................................................
N_data=1;
% Геометрические размеры (задают в мм)...............................
OA=40;
% Частота вращения ведущего звена (задают в об/мин) .................
n1=80;
%
% 1 СТРУКТУРНЫЙ АНАЛИЗ
% (См. раздел 1)
%
%
% 2 КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМА АНАЛИТИЧЕСКИМ МЕТОДОМ.
% МЕТОД ЗАМКНУТЫХ КОНТУРОВ
% (См. раздел 2)
%
% 2.1 Составляем векторное уравнение замкнутого контура механизма
% 2.2 Проекции векторного уравнения замкнутого контура на координатные оси
% ось x
eq1='a*cos(alpha0+omega1*t)-b*cosb-c';
% ось y
eq2='a*sin(alpha0+omega1*t)-b*sinb';
% 2.3 Решение системы 2-х уравнений
syms b betta t omega1 alpha0
eq1=subs(eq1,'b','a*tan(alpha0+omega1*t)');
eq2=subs(eq2,'b','a*tan(alpha0+omega1*t)');
betta=pi-asin(solve(eq2,'sinb'));
c=subs(solve(eq1,'c'),'cosb',cos(betta));
disp('Параметр c --->');disp(c);disp('');
disp('Параметр beta --->');disp(betta);
% 2.4 Закон движения ведущего звена 1
% Так как по условиям задачи ведущее звено вращается с постоянной угловой
% скоростью, то время одного оборота этого звена будет равно T1 в сек.
T1=60/n1;
disp(['Время одного оборота ведущего звена T1, с --> ', num2str(T1)]);disp(' ');
% Символьное задание закона движения ведущего звена как функции времени
% Omega1=Omega1(t)
omega1=sym(pi*n1/30);OmegaMin=0;
OmegaMax=subs(omega1,t,T1);
% график
subplot(2,1,1);
ezplot(inline(omega1),[0 T1/8 OmegaMin 1.1*OmegaMax]);
title '\omega_1=\omega_1(t)';
xlabel 't, с';
ylabel '\omega_1, рад/с';
% Функция времени угла поворота Alpha(t) ведущего звена
alpha=sym(int(omega1,t)+alpha0);
disp('Функция времени угла поворота ведущего звена --->');disp(alpha);
% задание начального положения ведущего звена в рад
alpha=subs(alpha,alpha0,pi/4);
% график
AlphaMax=subs(alpha,t,T1/8)*180/pi;
subplot(2,1,2);
ezplot(inline((180/pi)*alpha),[0 T1/8 0 AlphaMax]);
title '\alpha=\alpha(t)';
xlabel 't, с';
ylabel '\alpha, град';
% 2.5 Законы движения ведомых звеньев (звеньев 2 и 3)
% 2.5.1 Угол поворота второй части звена 1 (AB) - угол betta
% 2.5.2 Угловая скорость и ускорение звена 2 (B2B3) - omega2
omega2=diff(betta,t);
disp('Угловая скорость Omega2 --->');disp(omega2);
eps2=diff(omega2,t);
disp('Угловое ускорение Epsilon2 --->');disp(eps2);
% 2.5.4 Положение т.B2 относительно начала координат xOy определяется при
% помощи параметров a, alpha, b, betta, c
% 2.5.5 Скорость т.B3 относительно 2-й стойки - VB3B0
VB3B0=diff(c,t);
disp('Скорость VB3B0 --->');disp(VB3B0);
% 2.5.6 Ускорение т.В3 относительно 2-й стойки - WB3B0
WB3B0=diff(VB3B0,t);
disp('Ускорение WB3B0 --->');disp(WB3B0);
% 2.5.7 Графики кинематических величин звеньев 2 и 3
figure;
subplot(3,1,1);
betta=subs(betta,'omega1',pi*n1/30);
betta=subs(betta,'a',OA);
betta=subs(betta,'alpha0',pi/4);
ezplot(inline(180/pi*betta-'z'),[0 T1/8 120 200])
title '\beta=\beta(t)';
xlabel 't, с';
ylabel '\beta, град';
subplot(3,1,2);
omega2=subs(omega2,'a',OA);
omega2=subs(omega2,'alpha0',pi/4);
omega2=subs(omega2,'omega1',pi*n1/30);
ezplot(inline(omega2-'z'),[0 T1/8 1 11]);
title '\omega_2=\omega_2(t)';
xlabel 't, с';
ylabel '\omega_2, рад/с'
subplot(3,1,3);
eps2=subs(eps2,'omega1',pi*n1/30);
eps2=subs(eps2,'a',OA);
eps2=subs(eps2,'alpha0',pi/4);
ezplot(inline(eps2-'z'),[0 T1/8 -7 7]);
title '\epsilon_2=\epsilon_2(t)';
xlabel 't, с';
ylabel '\epsilon_2, рад/с^2'
figure;
subplot(3,1,1);
c=subs(c,'omega1',pi*n1/30);
c=subs(c,'a',OA);
c=subs(c,'alpha0',pi/4);
ezplot(inline(c-'z'),[0 T1/8 0 430]);title 'c=c(t)';
xlabel 't, с';
ylabel 'c, мм';
subplot(3,1,2);
VB3B0=subs(VB3B0,'omega1',pi*n1/30);
VB3B0=subs(VB3B0,'a',OA);
VB3B0=subs(VB3B0,'alpha0',pi/4);
ezplot(inline(VB3B0-'z'),[0 T1/8 0 3500]);
title 'V_{B_3}_{B_0}=V_{B_3}_{B_0}(t)';
xlabel 't, с';
ylabel 'V_{B_3}_{B_0}, мм/c';
subplot(3,1,3);
WB3B0=subs(WB3B0,'omega1',pi*n1/30);
WB3B0=subs(WB3B0,'a',OA);
WB3B0=subs(WB3B0,'alpha0',pi/4);
ezplot(inline(WB3B0-'z'),[0 T1/8 9000 77000]);
title 'W_{B_3}_{B_0}=W_{B_3}_{B_0}(t)';
xlabel 't, с';
ylabel 'W_{B_3}_{B_0}, мм/c^2';
% 2.5.8 Звено 3 движется поступательно и, следовательно,
% угловая скорость omega3=0 и угловое ускорение eps3=0.
% 2.6 Определение кинематических величин для заданного угла положения
% ведущего звена Alpha0
% 2.6.1 Задаем угол Alpha0 в град
% (угол задается в пределах от 45...90 град):
Alpha0=60;
disp('Заданный угол положения ведущего звена 1 - угол Alpha0, в град --->');
disp(Alpha0);
% Находим момент времени t0, когда ведущее звено 1 составит с осью x
% угол Alpha0
Alpha0=Alpha0*pi/180;
fx=sym(alpha-Alpha0);
r=solve(fx,t);
disp('Момент времени t0 в сек --->');
disp(r);
% 2.6.2 Модули скорости и ускорения точки B1 звена 1
VB1=subs(omega1,t,r)*OA/cos(Alpha0);
WB1n=(subs(omega1,t,r))^2*OA/cos(Alpha0);
WB1=WB1n;
disp('Модуль скорости точки B1 - VB1, в мм/с --->'); disp(VB1);
disp('Модуль ускорения точки B1 - WB1, в мм/с^2 --->'); disp(WB1);
% 2.6.2 Модули скорости и ускорений точки B звена 3 при его
% движении относительно звена 1
bb=OA*tan(alpha);
VB3B1=abs(subs(diff(bb,t),t,r));
WB3B1=abs(subs(diff(diff(bb,t),t),t,r));
disp('Модуль скорости VB3B1 ,в мм/с --->');
disp(eval(VB3B1));
disp('Модуль ускорения WB3B1, в мм/с^2 --->');
disp(eval(WB3B1));
% 2.6.3 Угловая скорость и угловое ускорение звена 2
disp('Угловая скорость звена 2 - omega2, в рад/с --->');
disp(eval(subs(omega2,t,r)));
disp('Угловое ускорение звена 2 - epsilon2, в рад/с^2 --->');
if abs(eval(subs(eps2,t,r)))<0.001,
disp(0);
else disp(eval(subs(eps2,t,r)));
end;
% 2.6.4 Модули скорости и ускорения точки В звена 3 и Кориолиса
Wc=2*abs(subs(omega1,t,r)*subs(diff(bb,t),t,r));
VB3=abs(subs(VB3B0,t,r));
WB3=abs(subs(WB3B0,t,r));
disp('Модуль скорости точки В3 - VB3, в мм/с --->');
disp(eval(VB3));
disp('Модуль кориолисова ускорения - Wc, в мм/с^2 --->');
disp(eval(Wc));
disp('Модуль ускорения точки B3 - WB3, в мм/с^2 --->');
disp(eval(WB3));
% 3 КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМА ВЕКТОРНО-ГРАФИЧЕСКИМ МЕТОДОМ.
% МЕТОД ПЛАНОВ СКОРОСТЕЙ И УСКОРЕНИЙ
% (См. раздел 3)
%
% 3.1 План положения механизма (См. соответствующий чертеж в приложении к данному документу)
% 3.2 План скоростей (См. соответствующий чертеж в приложении к данному документу)
% длины отрезков pa, ab2 и pb2 в мм
pa=25;ab3=50;pb3=43.3;
% коэффициент масщтаба kv плана скоростей в (мм/(с*мм))
kv=VB1/pa;
% скорости VB3B1 и VB3B0
VB3B1_2=kv*ab3;
VB3B0_2=kv*pb3;
disp(' ПЛАН СКОРОСТЕЙ');
disp('Масштабный коэффициент kv, мм/(с*мм) --->');disp(kv);
disp('Модуль скорости точки B1 - VB1, в мм/с --->'); disp(VB1);
disp('Модуль скорости точки B3 - VB3B0, в мм/с --->'); disp(VB3B0_2);
disp('Модуль скорости точки B3 относительно B1 - VB3B1, в мм/с --->'); disp(VB3B1_2);
disp('Углая скорость звена 2 - Omega2 (равна Omega1), в рад/с ---> ');disp(VB1/(OA/cos(Alpha0)));
disp('Omega2 направлена ---> против хода часовой стрелки');
% 3.3 План ускорений (См. соответствующий чертеж в приложении к данному документу)
% длины отрезков qa, ac, qb3, сb3 в мм
qa=12.5;
% ac=2*omega1*VB3B1/kw(=)2*VB1/(OA/cos(alpha))*VB3B1_2/kw
ac=50;qb3=87.5;cb3=86.6;
% коэффициент масщтаба kw плана ускорений в (мм/(с^2*мм))
kw=WB1n/qa;
% ускорения WB3B1, WB3B0 и Wc
WB3B1_2=kw*cb3;
WB3B0_2=kw*qb3;
Wc_2=kw*ac;
disp(' ПЛАН УСКОРЕНИЙ');
disp('Масштабный коэффициент kw, мм/(с^2*мм) --->');disp(kw);
disp('Модуль ускорения точки B1 - WB1, в мм/с^2 --->'); disp(WB1n);
disp('Модуль ускорения точки B3 относительно B1 - WB3B1, в мм/с^2 --->');
disp(WB3B1_2);
disp('Модуль кориолисова ускорения - Wс, в мм/с^2 --->'); disp(Wc_2);
disp('Модуль ускорения точки B3 - WB3B0, в мм/с^2 --->'); disp(WB3B0_2);
disp('Угловое ускорение звена 2 - Epsilon2, в рад/с^2 ---> ');disp(0);
disp('Epsilon2 не имеет направления из-за его отсутствия');
disp('WB3B0 направлено по направлению VB3B0');
disp('WB3B1 направлено по направлению VB3B1');
%
% 4 СРАВНЕНИЕ РЕЗУЛЬТАТОВ ДВУХ МЕТОДОВ
% (См. раздел 4)
%
disp(' ');
% 4.1 Скорость VB3B1 в мм/с
delta_VB3B1=((eval(VB3B1)-VB3B1_2)/eval(VB3B1))*100;
% 4.2 Скорость VB3B0 в мм/с
delta_VB3B0=((VB3-VB3B0_2)/VB3)*100;
% 4.3 Угловая скорость Omega2 в рад/с
absOmega2=abs(subs(omega2,t,r));
delta_Omega2=((absOmega2-VB1/(OA/cos(Alpha0)))/absOmega2)*100;
% 4.4 Ускорение WB3B1 в мм/с^2
delta_WB3B1=((eval(WB3B1)-WB3B1_2)/eval(WB3B1))*100;
% 4.6 Ускорение WB3B0 в мм/с^2
delta_WB3B0=((WB3-WB3B0_2)/WB3)*100;
% 4.8 Угловое ускорение Epsilon2 в рад/с^2
absEpsilon2=abs(eval(subs(eps2,t,r)));
if absEpsilon2<0.001, absEpsilon2=0;end;
delta_Epsilon2=((absEpsilon2-0)/absEpsilon2)*100;
if absEpsilon2==0, delta_Epsilon2=0;end;
disp(' СРАВНЕНИЕ РЕЗУЛЬТАТОВ ДВУХ МЕТОДОВ');
disp('Параметр Аналитика Графика Погрешность');
out1=eval(VB3B1);out2=VB3B1_2;out3=delta_VB3B1;
disp(['VB3B1, мм/с ',num2str(out1),' ',num2str(out2),...
' ',num2str(out3)]);
out1=eval(VB3);out2=VB3B0_2;out3=eval(delta_VB3B0);
disp(['VB3B0, мм/с ',...
num2str(out1),' ',num2str(out2),' ',...
num2str(out3)]);
out1=eval(absOmega2);out2=VB1/(OA/cos(Alpha0));out3=eval(delta_Omega2);
disp(['Omega2, рад/с ',num2str(out1),' ',...
num2str(out2),' ',num2str(out3)]);
out1=eval(WB3B1);out2=WB3B1_2;out3=eval(sym(delta_WB3B1));
disp(['WB3B1, мм/с^2 ',num2str(out1),' ',...
num2str(out2),' ',num2str(out3)]);
out1=eval(WB3);out2=WB3B0_2;out3=eval(delta_WB3B0);
disp(['WB3B0, мм/с^2 ',num2str(out1),' ',...
num2str(out2),' ',num2str(out3)]);
out1=absEpsilon2;out2=0;out3=eval(sym(delta_Epsilon2));
disp(['Epsilon2, рад/с^2 ',num2str(out1),' ',...
num2str(out2),' ',num2str(out3)]);

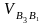 ,
мм/с
,
мм/с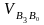 ,
мм/с
,
мм/с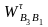 ,
мм/с2
,
мм/с2 ,
мм/с2
,
мм/с2