Примеры Короткое замыкание rl цепи.
П
усть
дана цепь, изображенная на рисунке. В
результате коммутации ключ переходит
из разомкнутого состояния в замкнутое.
Произойдет переходной процесс, потому
что до замыкания ключа ток через
протекал, а после замыкания ключа - нет.
Найдем ток, который протекает в этой
цепи. Запишем дифференциальное уравнение
для момента времени после коммутации:
.
Решение этого уравнение имеет вид
.
Так
как после замыкания ключа ток через
индуктивность не потечет (на источник
и резистор кинута закоротка),
.
Тогда общее решение нашего однородного
дифференциального уравнения имеет вид
,
где
определяется из характеристического
уравнения:
.
Показатель
экспоненты является безразмерной
величиной, тогда назовем величину
постоянной
времени RL
– цепи. Итак,
Определим постоянную интегрирования. Вспомним первый закон коммутации:
,
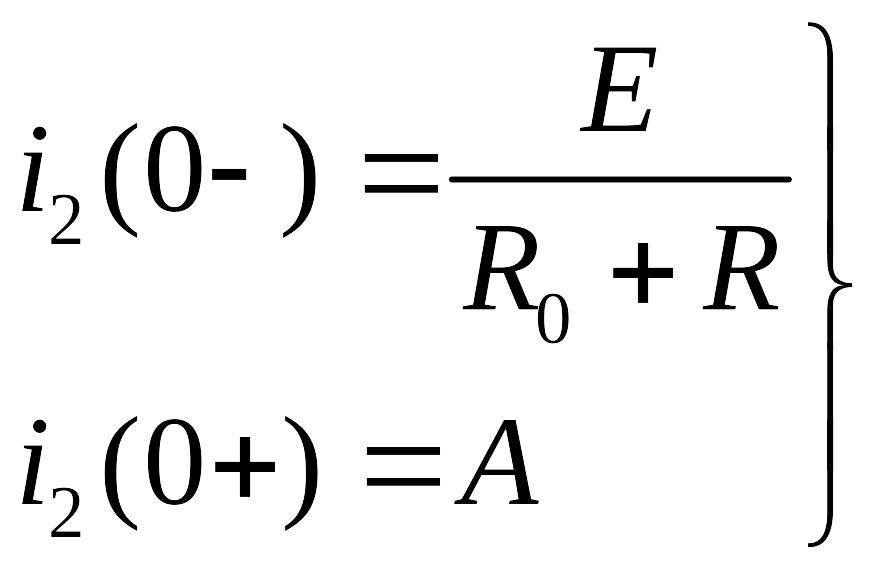
тогда искомый ток:
.
О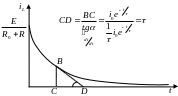
братим
внимание на постоянную
,
и посмотрим отрезок СD:
заметим, что проекция свободной
составляющей на ось времен в любой точке
равна
,
хотя на рисунке свободная составляющая
будет совпадать с переходным током.
В
рассмотренном переходном процессе на
сопротивлении рассеивается некоторая
энергия, причем
все время меняется:
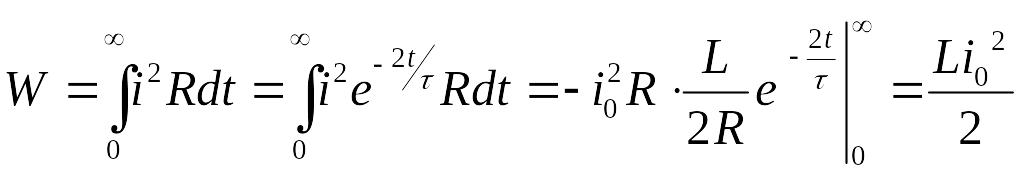
Вся энергия, накопленная на индуктивности, в результате переходного процесса рассеялась на сопротивлении.
Включение rl цепи на постоянное напряжение.
Д
ействуем
точно так же, как и в предыдущем примере.
Записываем 2 закон Кирхгофа и выражения
для свободного и принужденного токов:
Решая характеристическое уравнение, находим p и постоянную времени:
Пользуясь законами коммутации, находим постоянную интегрирования:
Записываем окончательное выражение для тока через индуктивность:
.
Т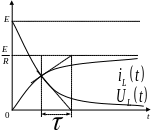
еперь
найдем напряжение на индуктивности:
;
Постоянная времени одинакова для всех процессов цепи!
Рассмотрим
поведение индуктивности в переходном
процессе. В начальный момент времени
,
т.е. все напряжение источника приложено
к зажимам индуктивности. Кроме того, по
1 закону коммутации, ток через индуктивности
до и после коммутации одинаков. Значит
индуктивность
в начальный момент времени после
коммутации ведет себя как источник
тока.
Включение rl цепи на источник синусоидального напряжения.
П
роделываем
те же ходы, что и в предыдущих случаях,
только с учетом синусоидального
принуждающего напряжения:
.
Второй закон Кирхгофа теперь имеет вид:
;
.
Принуждающая составляющая тока после коммутации является синусоидальной функцией той же частоты, что и источник, а амплитуда его не зависит от времени:
;
;
;
Как говорилось выше, свободная составляющая тока не зависит от входного воздействия:
;
;
Итак, общий ток в контуре после коммутации равен:
.
В начальный момент времени до коммутации
,
тогда
.
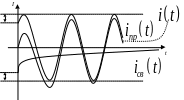
Ток в начальный момент времени равен нулю, значит характеристики свободного и принужденного токов начинаются со значений равных по модулю и противоположных по знаку (равные расстояния по оси ординат отмечены на графике). Результирующий график получается сложением двух графиков. Со временем характеристика результирующего тока бесконечно близко приближается к принуждающему воздействию.
Заметим,
что при
установившийся режим наступает сразу
после коммутации (свободная составляющая
будет отсутствовать, поскольку
).