
- •Гуманитарная
- •Дистанционное образование
- •Разработка управленческих решений юнита 2
- •Москва 2009
- •Литература
- •Фатхутдинов р.А. Управленческие решения: [Текст]: Учебник для вуЗов / Фатхутдинов р.А. – м.: Инфра-м, 2008
- •Чудновская с.Н. Управленческие решения: [Текст]: Учебник для вуЗов / Чудновская с.Н. – м.: эксмо, 2007.
- •1 Методы и модели подготовки и принятия решений (ппр)
- •1.1 Фундаментальные научные методы ппр
- •1.1.1 Системный подход
- •1.1.2 Воспроизводственный подход
- •1.1.3 Функциональный подход
- •1.1.4 Учет действия экономических законов
- •1.1.5 Жизненный цикл товара
- •1.2 Аналитические методы ппр
- •1.3 Дескриптивные методы ппр
- •1.4 Моделирование
- •1.5 Технология принятия управленческого решения
- •1.6 Диалоговые компьютерные системы и технологии интеллектуальной поддержки ур
- •2 Условия неопределенности и риска
- •3 Технология ппр в условиях неопределенности и риска
- •3.1 Способы оценки степени риска. Размер возможного ущерба
- •3.2 Управление риском
- •3.3 Способы снижения степени риска
- •4 Процесс принятия управленческих решений различных типов
- •4.1 Особенности подготовки ур в области инвестиционной деятельности
- •4.2 Некоторые ур, связанные с неопределенностью выбора результата
- •4.3 Влияние индивидуальных особенностей лпр на решение
- •2. Задание:
- •3. Дайте краткую характеристику “областей” риска:
- •4. Дайте краткую характеристику ур в зависимости от характера лпр:
- •1.2. Задания для самостоятельной работы
- •1.2.1. Задача
- •1.2.2. Задача
- •2.2. Задания для самостоятельной работы
- •2.2.1. Задача
- •2.2.2. Задача
- •3.2. Задания для самостоятельной работы
- •3.2.1 Задача
- •3.2.2. Задача
- •4.2. Задания для самостоятельной работы
- •4.2.1. Задача
- •4.2.2. Задача
- •5.2. Задания для самостоятельной работы
- •5.2.1. Задача
- •5.2.2. Задача
- •Разработка управленческих решений юнита 2
2. Задание:
2.1. Восстановите пропущенные элементы в схеме:
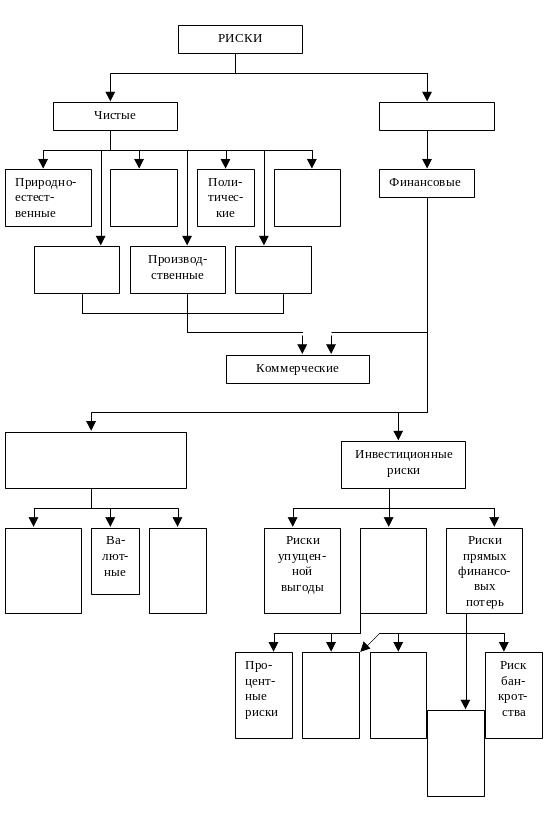
2.2. Восстановите пропущенные элементы в схеме:

2.3. Восстановите пропущенные элементы в схеме:

3. Дайте краткую характеристику “областей” риска:
№ |
Область |
Характеристика |
1 |
Безрисковая |
|
2 |
Минимального риска |
|
3 |
Повышенного риска |
|
4 |
Критического риска |
|
5 |
Недопустимого (катастрофического) риска |
|
4. Дайте краткую характеристику ур в зависимости от характера лпр:
№ |
Вид решений |
Характеристика |
1 |
Чисто интуитивные |
|
2 |
Уравновешенные |
|
3 |
Импульсивные |
|
4 |
Основанные на суждении |
|
5 |
Инертные |
|
6 |
Рискованные |
|
7 |
Осторожные |
|
8 |
Рациональные |
|
ТРЕНИНГ КОМПЕТЕНЦИЙ
Компетенция №1. Расчет дисперсии.
Пример решения типовой задачи
Условие
Рассчитайте дисперсию при вложении капитала в мероприятие А:
Номер события |
Полученная прибыль, тыс. руб., х |
Число случаев наблюдения |
1 2 3
|
250 200 300
|
48 36 36
|
Решение
№ п\п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Определение х – среднего ожидаемого значения |
По формуле простой средней арифме-тической (250 + 200 + 300) : 3 = 250 |
2 |
Определение отклонений ожидаемого значения каждого случая наблюдения от среднего ожидае-мого значения (х – ) |
Для события 1: 250-250 = 0; Для события 2: 200-250 = -50; Для события 3: 300-250 =+50 |
3 |
Определение квадратов отклонений ожидаемого значения каждого случая наблюдения от сред-него ожидаемого значения (х – ) 2 |
Для события 1: 02 = 0; Для события 2: (-50)2 = 2500; Для события 3: (+50)2 = 2500 |
4 |
Определение произведений квадратов откло-нений ожидаемого значения каждого случая наблюдения от среднего ожидаемого значения на число случаев наблюдения (частоту) (х – ) 2n |
Для события 1: 0 х 48 = 0; Для события 2: 2500 х 36 = 90000; Для события 3: 2500 х 36 = 90000 |
5 |
Определение суммы произведений квадратов отклонений ожидаемого значения каждого случая наблюдения от среднего ожидаемого значения на число случаев наблюдения (частоту) (х – ) 2n |
Суммированием 0 + 90000 + 90000 = 180000
|
6 |
Определение суммы частот n |
48 + 36 + 36 = 120 |
7 |
Определение дисперсии по формуле
|
180000: 120 = 1500 |

