3.2.Кодирование в дискретных каналах без шумов

Общие принципы кодирования

Дискретным m-ичным каналом без шумов называется канал, в котором сигналы на входе А(t) и выходе B(t) являются последовательностями дискретных случайных величин - символов с основанием кода m, причем входной и выходной сигналы связаны взаимно однозначно (см. рис. 3.1).

Пропускная способность такого канала равна наибольшей возможной энтропии сигнала A(t) на его входе

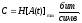
Из (2.4.5) имеем

(3.2.1)

где F_k- частота следования символов в канале, симв/с.

Пусть Х⁽¹⁾, Х⁽²⁾, …- последовательность символов s-ичного источника сообщений при многократном независимом выборе. Тогда скорость создания информации равна

Н=Н(Х)F_и , (3.2.2)

где F_и- частота следования символов источника, Н(Х)-энтропия алфавита источника.

Функции кодирующего устройства заключаются в том, чтобы каждой из букв s-ичного алфавита источника поставить в соответствие кодовое слово, состоящее из букв m-ичного алфавита, используемого для передачи по каналу.

Кодирующее устройство должно удовлетворять двум основным требованиям:

1.Обеспечить безошибочную передачу информации, т.е. взаимно однозначное соответствие между X(t) и A(t) (см. рис.3.1).

2.Осуществить кодирование наиболее экономным образом (с минимальной избыточностью).

Для выполнения первого требования необходимо, во-первых, чтобы различным буквам алфавита источника соответствовали различные кодовые слова, и, во-вторых, была предусмотрена возможность разделения кодовых слов при их последовательной передаче.

Для осуществления возможности разделения кодовых слов применяется одна из следующих мер:

1. Использование специальной буквы.

2. Применение кодовых слов одинаковой длины без разделительных букв - равномерное кодирование.

3. Кодовая таблица составляется так. Чтобы никакое кодовое слово не являлось началом другого более длинного.

Требование экономичности заключалось в том, что необходимо добиваться при кодировании минимальной средней длины кодового слова

, (3.2.3)

где l_k- длина k-го кодового слова с учетом разделительной буквы, если таковая используется.

Средняя длина кодового слова ограничена снизу, так как для безошибочной передачи информации необходимо выполнение соотношения НС. Это обстоятельство сформулировано в теореме Шеннона о кодировании в дискретных каналах без шумов.

Теорема. При кодировании множества сигналов с энтропией Н(Х) при условии отсутствия шумов средняя длина кодового слова не может быть меньше, чем Н(Х)/log m, где m-основание кода. Если вероятности сигналов не являются целочисленными отрицательными степенями числа m, то точное достижение указанной нижней границы невозможно, но при кодировании достаточно длинными блоками к ней можно сколь угодно приблизиться.

Существует несколько способов, позволяющих получать коды с малой избыточностью, причем все они обладают следующими свойствами:

1.Более вероятным буквам источника соответствуют более короткие кодовые слова (принцип статистического кодирования).

2.Никакое кодовое слово не является началом другого, более длинного.

3.Все буквы алфавита, используемого для передачи по каналу, приблизительно равновероятны.

4.Символы в последовательности на входе кодера практически независимы.

Наилучшим среди этих кодов является код, предложенный Д.А.Хаффманом.

Код Хаффмана

Кодирование по методу Хаффмана осуществляется следующим образом:

1. s букв алфавита источника располагаем в порядке убывания их вероятностей.

2. Выбираем целое число m₀ такое, что

где а – целое положительное число.

При кодировании в двоичном канале m₀=m=2.

Производим первое сжатие алфавита, т.е. группируем вместе m₀ букв алфавита источника, имеющих наименьшие вероятности, и обозначим навой буквой. Вычисляем общую вероятность такого сгруппированного подмножества букв.

3.Буквы нового алфавита полученного в результате первого сжатия, снова располагаем в порядке убывания вероятностей.

4.Производим второе сжатие этого алфавита, т.е. снова группируем вместе m букв, имеющих наименьшие вероятности, и обозначим новой буквой. Вычисляем общую вероятность сгруппированного подмножества букв.

5.Буквы нового алфавита, полученного на 4-м шаге, располагаем в порядке убывания вероятностей.

6.Осуществляем последовательное сжатие алфавита путем повторения операций 4 и 5, пока в новом алфавите не останется единственная буква.

7.Проводим линии, который соединяют буквы, образующие последовательные вспомогательные алфавиты. Получается дерево, в котором отдельные сообщения являются концевыми узлами. Соответствующие им кодовые слова получаем, если приписать различные буквы m-ичного алфавита ветвям, исходящим из каждого промежуточного узла.

Код Хаффмана имеет среднюю длину кодового слова меньшую (или равную), чем любой другой код.

Код Шеннона-Фано

Кодирование осуществляются следующим образом:

1.s букв алфавита источника располагаем в порядке убывания вероятностей.

2.Делим алфавит источника на m групп так, чтобы общие вероятности букв в каждой из групп были примерно равны. В качестве первого символа кодового слова выбираем 0,1,…,m-1, в зависимости от того, в которой из групп оказалась кодируемая буква.

3.Каждую из групп снова разбираем на m примерно равновероятных подгрупп, и в качестве второго символа кодового слова выбираем 0,1,…, в зависимости от того, в которой из групп оказалась кодируемая буква.

4.Такое разделение на все более мелкие группы проводится до тех пор, пока в каждой из групп не окажется по одной букве.

Блоковое кодирование

Выше были рассмотрены способы побуквенного кодирования, когда каждой букве на выходе источника приписывалось свое кодовое слово. Таковой способ кодирования позволяет достигнуть минимальной средней длины кодового слова, равной Н(Х)/log m, только в том случае, когда вероятности букв являются отрицательными целочисленными степенями числа m. Если вероятности не удовлетворяют этому требованию, избыточность при побуквенном кодировании может оказаться недопустимо большой. В таком случае применяют блоковое кодирование.

При кодировании блоками по k букв, прежде всего, строят вспомогательный алфавит, состоящий из N=s^k букв, так что каждой букве этого алфавита соответствует своя комбинация (блок) из k букв алфавита источника. Вероятность буквы z_ij…_q вспомогательного алфавита, соответствующей комбинации x_ix_j…x_q, вычисляется по формуле

p(z_ij…_q) = p(x_i) p(x_j)…p(x_q). (3.2.4)

Далее буквы вспомогательного алфавита располагаются в порядке убывания вероятностей, и осуществляется кодирование методом Шеннона-Фано или Хаффмана.

Таким образом, кодирующее устройство при блоковом кодировании разбивает последовательность букв на выходе источника на блоки длиной в k букв каждый, и генерирует последовательность кодовых слов, соответствующих каждому из блоков.