Ответы, решения, методические указания

1.Сигналы и помехи в системах

передачи информации

1.1. 5,7. 1.2. 0,154 Вт. 1.3. Нет. 1.4. p(x₁/y) = 0,00247; p(x₂/y) = 0,99753.

1.5. t=4^o ; p(t₁) = 1/10, i=1, …, 10.

1.6. 1,33. 1.7. p_i=0,0000; 0,0000; 0,0014; 0,0214; 0,1359; 0,3413; 0,3413; 0,1359; 0,0214; 0,0014.

1.8. 24·10⁶ . 1.9. Нет. 1.10. а) 0,2; б)да, являются. 1.11. 2,89. 1.12. 0,26.

1.13.

1.14.

15. a)

б) в)

16. x*=6,93 В . 1.17.

2.Дискретные каналы

2.1.Собственная информация. Взаимная информация

1. 2 бит. 2.1.2. 1 бит. 2.1.3. 2,58 бит. 2.1.4. 0,415 бит. 2.1.5. 1,78 бит. 2.1.6. 8,5 бит. 2.1.7. 0,18 бит. 2.1.8. а) 2,18 бит; б) 3,7 бит.

2.1.9. 1) а) 1 бит.; б) 0 бит.; в) -; 2)-log 5/2 бит. 2.1.10. 26,910⁸ бит.

2.1.11. I(x₁;y₂) = - 0,585 бит; I(x₂;y₂) = 0,52 бит; I(x₃;y₁) = -0,07 бит.

12. I(x₁;y₃) = - 1,8 бит; I(x₃;y₁) = -1 бит.

1. I(x₁;y₃) = - 0,58 бит; I(x₂;y₂) = 0,52 бит.

14. I(x₁;0) = 0,42 бит; I(x₂;1/0) = 1,58 бит; I(x₂;0/01) = 1 бит.

2.1.15. I(x₃;1) = 2 бит; I(x₃;0/1) = 0 бит; I(x₃;1/10) = 1бит.

2.1.16. 1.42 бит.

2.2.Средняя собственная информация (Энтропия)

2.2.1. 5 бит. 2.2.2. 1,84 бит; 0,08. 2.2.3. 4. 2.2.4. 1,5 бит.

2.2.5. a) б) 1,81 бит.

2.2.6. Н₁<Н₂ . 2.2.7. Н = 0,88 бит; R = 0,12. 2.2.8.Н=1,685 бит; R = 0,16. 2.2.9. 814 бит. 2.2.10. 296 бит/с. 2.2.11. 92,2 бит. 2.2.12.0,837 бит.

1. Указание. Воспользоваться неравенством Иенсена.

15. Н_А<H_В , т.е. степень определённости качества связи с узлом А больше, чем с узлом В.

16. 139 км. 2.2.16. 44 % .2.2.17. а) 15 ноября; б) 15 июня.

2.3.Средняя взаимная информация

1. 0,21 бит/букву. 2.3.2. 2,8 бит/букву. 2.3.3. 2,2 бит.

2.3.4. 0,91 бит/симв. 2.3.5. а) 0,484 бит/симв.; б) 0,205 бит/симв.

6. 0,11 бит.

7. а) I(X;Y) = - [(1- )(1- )+(1- )] log [(1- )(1- )+(1- )]-

-+(1- )] log [+(1- )]+[ log +(1- )log (1- )]+

+ [(1- ) log +(1- )log (1- )]; б) 0,12 бит/символ.

8. 0,2 бит. 2.3.9. 15 октября. 2.3.10. 0,04 бит. 2.3.11. 0.3.12.0,84 бит. 2.3.13. 0,21 бит. 2.3.14. 0,13 бит.

2.3.14. а) 2^-n+1 ;

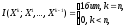
так как первые n-1 символов статистически независимы, а последний n-й символ полностью определяется предыдущими.

2.3.17. I(X;Y) = - 0,9 [p log p + (1-p) log(1-p)] бит/символ, где р – вероятность символа x₁ на входе.

2.4.Энтропийные и информационные характеристики случайных последовательностей

2.4.1.а)2,58 бит/симв =0,516 бит/с; б) 0,86 бит/симв =0,516 бит/с;в)31 бит.

2.4.2. 36,2. 2.4.3. а)10 бит/симв; б) 1бит/симв; в) 1бит/симв; г)10 бит/симв;

д)0,9886 бит/симв. 2.4.4. а) 0,333 бит/симв; б) 0,99994 бит/симв.

2.4.5. а) 0,52 бит/симв. 2.4.6. 1,585 бит/симв. 2.4.7. 1,37 бит/симв.

2.4.8. а) 1,56 бит/симв; б) H=0,661 бит/симв.; R=58%.

9. I=0,2 бит; R=80%. 2.4.10. 0,881 бит/сообщение.

Л и т е р а т у р а

1. Ю.П.Акулиничев, В.И.Дроздова. Сборник задач по теории информации. Издательство Томского университета, Томск, 1976, 140 с.

2. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники. - М: "Энергия", 1971, 424 с.

3. Дмитриев В.И. Прикладная теория информации: Учеб. для студ. вузов, - M,: Высшая школа, 1989, 320 с.

4. Основы теории информации и кодирования. Кузьмин И.В., Кедрус В.А. Киев, издательское объединение "Вища школа", 1977, 280 с.