- •Методический материал для подготовки к зачету по предмету: «Анализ данных»
- •Описательная статистика
- •Критерий Хи-квадрат
- •3. Сравнение средних. Дисперсионный анализ
- •1. Общая постановка задачи
- •2. Понятие зависимой переменной и фактора
- •3. Тип данных для дисперсионного анализа
- •4. Однофакторный и двухфакторный дисперсионный анализ
- •5. Формулировка гипотез для двухфакторного анализа
- •6. Эффекты взаимодействия
- •8. Критерий Левене об однородности дисперсий.
- •9. Ограничения дисперсионного анализа и теста Стьюдента
- •10. Зависимые и независимые выборки
- •11. Непараметрические аналоги (Критерий знаков, Манна-Уитни, Вилкоксона, Краскела-Уоллиса, Фридмана).
- •4. Регрессионный анализ
- •6 Этапов регрессионного исследования
- •Уравнение линейной регрессии
- •Значимость коэффициентов линейной регрессии
- •Коэффициент детерминации
- •Кластерный анализ
- •Понятие расстояния
- •Основные метрики, используемые при кластеризации.
- •Расстояние между кластерами
Кластерный анализ
Общая идея заключается в последовательном объединении группируемых объектов: сначала самых близких, затем - все более отдалённых друг от друга. Процедура классификации состоит из последовательных шагов, на каждом из которых производится объединение двух ближайших групп, объектов, кластеров (термин «кластер» переводится с английского, как «гроздь»; он обозначает группу объектов, обладающих общими свойствами). Результаты кластерного анализа удобно изображать в виде «дерева»- иерархической структуры (дендрограммы), содержащей n-уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров. В принципе, кластеров можно строить сколько угодно много. При этом кластерный анализ позволяет не только «разбивать» совокупности объектов на группы, но и измерять меру близости этих групп.
Понятие расстояния
Каждая единица совокупности в кластерном анализе считается «точкой в признаковом пространстве». Значение каждого из признаков у данной единицы совокупности служит ее координатой в этом «пространстве» по аналогии с координатами точки в нашем реальном трехмерном пространстве. Таким образом, «признаковое пространство» – это область варьирования всех признаков совокупности изучаемых явлений. Если мы уподобим это пространство нашему пространству, имеющему Евклидову метрику, то получим возможность измерять «расстояния» между точками признакового пространства. Эти расстояния называют «Евклидовыми». Их вычисляют по тем же правилам, как и в обычной Евклидовой геометрии. На плоскости (то есть в «двухмерном пространстве») расстояние между точками А и В равно, как показано на рисунке, корню квадратному из суммы квадратов разностей параметров рассматриваемых точек по осям координат – на основании знаменитой теоремы Пифагора.
Кластер — объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определёнными свойствами.
Основные метрики, используемые при кластеризации.
Основные типы метрик при кластер-анализе |
|||
N |
Наименование метрики |
Тип признаков |
Формула для оценки меры близости (метрики) |
1 |
Эвклидово расстояние |
Количественные |
|
2 |
Мера сходства Хэмминга |
Номинальные (качественные) |
|
3 |
Мера сходства Роджерса–Танимото |
Номинальные шкалы |
|
4 |
Манхэттенская метрика |
Количественные |
|
5 |
Расстояние Махалонобиса |
Количественные |
|
6 |
Расстояние Журавлева |
Смешанные |
|
Процент
несогласия. Эта мера
используется в тех случаях, когда данные
являются категориальными. Это расстояние
вычисляется по формуле: расстояние(x,y)
= (Количество xi
![]() yi)/
i
yi)/
i

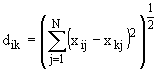
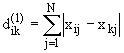
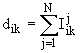 ,
где
,
где