МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М.В. ЛОМОНОСОВА СОЦИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

Методический материал для подготовки к зачету по предмету: «Анализ данных»

Выполнила студентка

вечернего отделения

31 группы

Пчёлкина К.К.

Ст. преп., к.физ-матн.:

Медведев К.В.

Москва, 2012 г.

1. Описательная статистика

Мода - характеризует величину признака, появляющуюся наиболее часто по сравнению с другими величинами данного признака. Мода но­сит относительный характер, и необязательно, чтобы большинство рес­пондентов указало именно эту величину признака.

Медиана–1) характеризует значение признака, занимающее срединное место в упорядоченном ряду значений данного признака;

– 2) значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части.

Среднее - чаще всего рассчитывается как средняя арифметическая величина. При ее вычислении общий объем признака поровну распределяется между всеми единицами совокупности.

Размах- разность между наибольшим значением набора данных и наименьшим.

(R= x_max - x_min)

Квартильный размах- разница между третьим и первым квартилем и вычисляется по формуле: IQR= Q3-Q1. Между Q1 и Q3расположены50% всех данных.

Квартили- значения, которые делят вариационный ряд на четыре равные части.Ниже первого квартиля расположено 25% всех данных. Между первым и вторым квартилем также расположено 25% данных. Второй квартиль совпадает с медианой.

Дисперсия- дисперсия выборки – среднее арифметическое квадратов отклонений значений выборки от выборочного среднего.

Стандартное отклонение— характеризуют среднее отклонение от среднего значения выборки. Это значение можно представить как среднее расстояние, на котором находятся элементы от среднего элемента выборки.

Коэффициенты корреляции Пирсона и Спирмена

Коэффициент корреляции Спирмена(Spearmanrankcorrelationcoefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги.

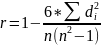
«-1» – сильно отрицательная связь

«1»–сильная положительная связь

«0» - связи нет

«0,5» - барьерное значение, т.е. при r (-0,5; 0,5) – незначительная связь

Коэффициент корреляции Пирсонахарактеризует наличие только линейной связи между признаками X и Y.Онустанавливает тесноту этой связи. Величина коэффициента может быть от -1 до 1. Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально.

Ф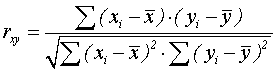 ормула предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.

Проверка нормальности распределения (skewness и kurtosis, гистограмма с нормальной кривой)

Ассиметрия (Skewness)

1) Если распределение симметрично, ассиметрияравна«0». В этом случае совпадают значение Моды, Медианы и Среднего.

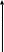
- Мода, Медиана и Среднее

2) Если одно или несколько значений существенно превышают остальные, то ассиметрияположительная. Среднеее больше Моды и Медианы.

- Мода, Медиана и Среднее

3) Если одно или несколько значений существенно меньше остальных, то ассиметрияотрицательная. Среднее меньше Моды и Медианы.

- Мода, Медиана и Среднее

Коэфициентассиметрии измеряется в пределах от -3 до 3.

K urtosis – крутость кривой распределения. Определяется сопоставлением кривой с кривой стандартного нормального распределения.

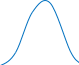
- вероятность выпадения значения рядом со средним больше

- стандартное распределение

- вероятность выпадения значения рядом со средним меньше

В SPSS проверка на нормальность распределения находится в меню:

«Statistics» => «Distribution»

Показатель		Ошибка
| Skewness|	<	2 * S.E.S.	} – при таком исходе распределение считается нормальным
| Kurtosis|	<	2 * S.E.K.
* если хоть один знак будет другой, то такое распределение – ненормальное Гистограмма с нормальной кривой. Меню Charts команды Frequencies. -выбираемдиаграмму (bar, pie, Histograms, None) -withnormalcurve – с нормальной кривой -значения (абсолютные или относительные). Способы проверки распределения на нормальность: Построение графика (гистограмма с нормальной кривой; визуальный анализ) Вычисление коэффициента асимметрии (эксцесс, куртозис); шаманское правило.

Вариационный ряд-ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им частотой, частостью.

Частотная таблица

Частота (frequency) – количество наблюдений, в которых признак принимает определенное значение или находится в определенном интервале.

Распределение частот (frequencydistribution) показывает частоты во взаимосвязи с результатами наблюдений.

Двухмерная частотная таблица (таблица сопряженности)– построение таблиц сопряженности признаков – статистический метод, который одновременно характеризует две или больше переменных. Строки соответствуют значениям одной переменной, а столбцы - значениям другой переменной. Обычно табулируются номинальные, категориальные переменные или переменные с относительно небольшим числом значений.

Суть заключается в создании таблиц сопряженности признаков, отражающих совместное распределение двух или больше переменных с ограниченным числом категорий или определенными значениями.

(«Contingency table»s, «cross-tabulation»)

Сумма частот по строке N(xi) называется маргинальной частотой строки; сумма частот по столбцу N(yj)- маргинальной частотой столбца

Накопленные частоты- это число, полученное последовательным суммированием частот в направлении от первого интервала к последнему, до того интервала включительно, для которого определяется накопленная частота. Накопленные частоты обозначим nxi.Показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.

Кумулята (график накопленных частот) – график  распределения накопленных частот для порядковых и количественных переменных (также: шкала измерительная). Имеет вид возрастающей ломаной линии. Для дискретной переменной линия кумуляты соединяет точки, абсциссами которых являются значения переменной, ординатами - значения соответствующих им накопленных частот. Для количественной переменной частот в качестве абсцисс используются верхние точные границы интервалов.

Валидные проценты–1) доля численного значения признака от общей численности совокупности. Используется для всех видов шкал.

2) это значения без учета пропущенных ответов. Значимые проценты.

Пропущенные значения–в SPSS допускаются два вида пропущенных значений:

1) Пропущенные значения, определяемые системой (System-definedmissingvalues): Если в матрице данных есть незаполненные численные ячейки, система SPSS самостоятельно идентифицирует их как пропущенные значения. Этот факт отображается в матрице данных с помощью запятой (,).

2) Пропущенные значения, задаваемые пользователем (User-definedmissingvalues): Если в определенных случаях у переменных отсутствуют значения, например, если на вопрос не был дан ответ, ответ неизвестен, или существуют другие причины, пользователь может с помощью кнопки Missing объявить эти значения как пропущенные. Пропущенные значения можно исключить из последующих вычислений.

Самым простым методом заполонения пропущенных значений является заполнение средним значением (модой, медианой или средним арифметическим - в зависимости от шкалы, по которой измерена переменная с пропусками), найденным по имеющимся данным.

В отличие от первой процедуры, метод ближайшего соседа предполагает, что пропуски будут заполнены различными значениями. Мерой похожести в данном случае выступает декартово расстояние между точками, координаты которых заданы значениями переменными, по которым сравниваются строки-наблюдения. Чем меньше декартово расстояние, тем более близкими являются объекты.

При использовании метода многомерной регрессии строится модель линейной зависимости переменной, в которой необходимо заполнить пропуски, от ряда других имеющихся признаков.

Коробковая диаграмма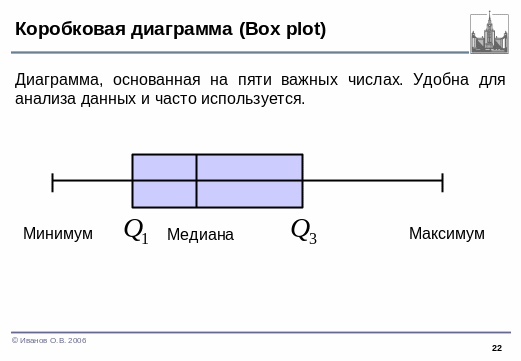

Отбор значений в SPSS - это выборнаблюдений по определенным критериям; так, например, при опросе избирателей.

Перевзвешивание- перевзвешивание выборочных результатов сводится к расчету по каждому значению контролируемого признака весового коэффициента, определяемого как отношение планового числа анкет к реально полученному. Затем количество анкет приводится в соответствие с вычисленным весом. Весовой коэффициент k > 1 означает, что анкет с данным значением признака в массиве оказалось недостаточно, и каждая из них используется в обработке более одного раза, иными словами объем таких анкет увеличивается в k раз. Если k < 1 объем анкет соответственно уменьшается, анкеты, которых "перебор", случайным образом отсекаются и исключаются из обработки. Весовой коэффициент k = 1 говорит о том, что данная группа анкет участвует в обработке без изменений.

М-оценки- в тех случаях, когда данные не подчиняются нормальному распределению и не помогают никакие преобразования, могут оказаться полезными М-оценки, позволяющие оценить положение центра распределений для каждой из групп, и процентили, характеризующие разброс распределений. Полезно посмотреть на пять наименьших и пять наибольших значений в пределах каждой из групп с названиями стран.