1.3 Вибір методу вирішення основної задачі

Користувач власноручно задає розміщення ємкостей на формі та, тим самим, регулює їх кількість. Для роботи програми на основі елементів, що знаходяться на полотні, буде складатися таблиця суміжності. На основі цієї таблиці буде прохід алгоритму Дейкстри по вигідним відносно умови полям. Розмір таблиці буде рівним (N+1)*(N+1), де N – кількість об’єктів на формі, а ще одне поле та ще один стовпчик відводяться під найменування (тобто сервісні області з підказками по напрямкам відношень, що допоможуть користувачеві зорієнтуватись під час введення даних в таблицю).

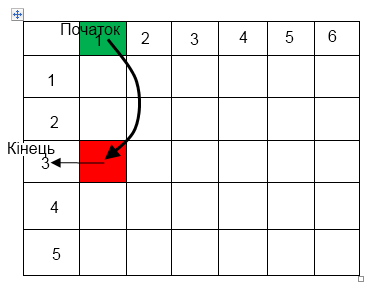
Рисунок 1.2 – Схематичне зображення таблиці

На рисунку 1.2 зображено приклад схеми відношення елементу відповідно до його значення. Вихідні об’єкти, тобто ті об’єкти, з яких переливаємо, знаходять вгорі таблиці. Відповідно рисунку 1.2 з елемента під іменем «1» (виділений зеленим кольором) здійснюється переливання в елемент під іменем «3» (виділено червоним кольором). Потім, якщо даний елемент задовольняє умову, тобто переливання в нього займає найменший час серед усіх можливих, від рядка з номером кінцевого елемента переходимо до стовпчика з відповідним номером. Слід також зазначити, що пошук мінімального часу переливання серед можливих елементів здійснюється шляхом порівнювання всіх значень часу переливання для вибраного елементу в усі інші.

Непотрібні значення автоматично будуть виключатись. Наприклад, переливати з останньої посудини в першу абсолютно не містить ніякого сенсу. Аналогічно й переливання в ту ж посудину, переливання з будь-якої іншої посудину в початкову (адже якщо з початкової в кінцеву невигідно – то нема сенсу переливати в початкову) та переливання з кінцевої посудини в будь-яку іншу теж хибне. Всі ці значення потрібно автоматично обнуляти та блокувати, адже користувачу вони явно непотрібні, а на роботу програми ніяким чином не впливають.

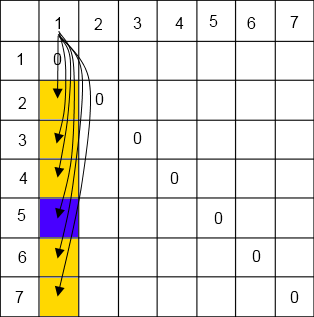
Рисунок 1.3 – Пошук мінімального

На рисунку 1.3 зображено пошук мінімального часу переливання. Жовтим кольором відмічені ті області, які проходитимуться, а нульові значення ігноруватимуться. Фіолетовим позначено знайдене мінімальне (для прикладу). Аналогічно і для всіх інших стовпців.

А тепер, власне, алгоритм. Позначимо мінімальне для кожного із стовпчиків через MIN, а кількість загальну елементів через N. Також, для роботи потрібна змінна, яка зберігатиме суму мінімальних значень – це дасть змогу орієнтуватись в тому, чи є пройдений шлях вигідним і витрачений час на нього менший за час переливання з початкової посудини в останню (позначимо цей час через R). Також, потрібна буде змінна, що вказує, в якому стовпчику знаходимось на даному етапі виконання. На початку виконання алгоритму знаходимось у першому стовпчику та другому рядку – це і є вихідна позиція, з якої будемо рухатись по таблиці. Шукаємо найменше значення серед усіх (MIN на цьому етапі буде дорівнювати будь-якому ненульовому значенню із даного, тобто першого, стовпця). Знайшовши найменше числове значення – запам’ятовуємо номер рядка, в якому воно знаходиться. Перевіривши всі елементи і знайшовши найменше, тобто MIN, перевіряємо чи менше це значення в сумі із S (на початку S=0), тобто чи S + MIN < R. Якщо виявиться що не менше – закінчуємо проходження та, очевидно, робимо висновок, що найвигіднішого шляху крім переливання з початкової посудини в останню нема. Якщо ж все-таки менше, тоді S збільшуємо на знайдене значення MIN та переходимо у стовпець під номером стрічки, де знаходилось найменше значення MIN. Для нового стовпця відразу перевіряємо, як і у попередньому, чи сума часу переливання з даної ємкості в кінцеву та значення S буде меншим, якщо менше – то це і є шуканий шлях, інакше – шукаємо в цьому стовпчику мінімальне значення. Знайшовши – перевіряємо, чи знайдене нове MIN в сумі із S менше R, якщо менше – переходимо у стовпчик під номером стрічки, в якій знаходилось мінімальне значення і виконуємо знову такі ж операції по пошуку мінімального значення в стовпчику та перевірки, чи менше воно в сумі із S за орієнтоване значення R до поки не знайдеться така місткість, з якої час переливання в останню посудину в сумі із S (затраченим часом на пошук) буде меншим ніж час переливання із першої посудини в останню (тобто за R). А якщо ж все-таки не знаходимо найкоротшого шляху – робимо висновок, що вигіднішого часу за час переливання із першої посудини в останню нема.

Для прикладу, побудуємо таблицю відповідного часу переливання для п’яти елементів, як це зображено на рисунку 1.4.

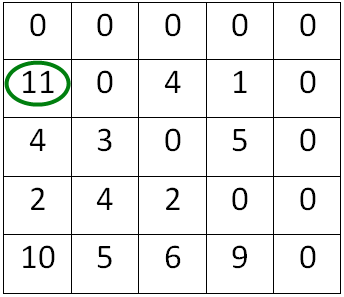
Рисунок 1.4 – Приклад таблиці відповідностей

Також, на рисунку зеленим кольором обведене значення, яке при початку виконання алгоритму буде мінімальним (MIN). Згідно рисунку 1.5 перевіряємо, чи S (сума мінімальних значень, на початку рівно нулю) і часу переливання відразу в кінцеву посудину не менше R. В даному випадку: 0 + 11 > 10, отже шукаємо мінімальне значення. 11 менше 4 і 4 менше 2, тому MIN = 2.

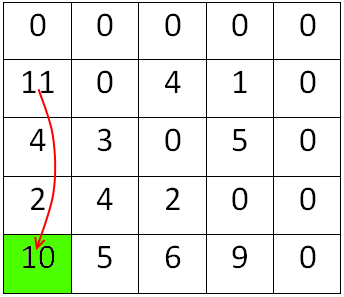
Рисунок 1.5 – Перевірка першої умови

Мінімальне значення знаходиться в 4-тому рядку, тому переходимо в 4-тий стовпчик а S збільшуємо на MIN (S = S + 2 = 0 + 2 = 2). Перейшовши, відразу надаємо MIN перше ненульове значення – в даному випадку це буде 1 та перевіряємо, чи сума S і часу переливання в кінцеву посудину не менша за R, тобто: 2 + 9 = 11, а 11 > 10. Умова не справдилась, тому шукаємо мінімальне значення, як це зображено на рисунку 1.6.

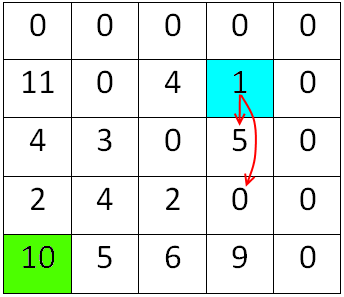
Рисунок 1.6 – Пошук мінімального в 4-тому стовпчику

Згідно рисунку 1.6: 1 менше 5, а 0 не розглядаємо, тому мінімальним залишається значення 1. Отже, MIN знаходиться в 2-гому рядку – переходимо до другого стовпчику та збільшуємо S на значення MIN (S = S + 1 = 4). В цьому стовпчику проводимо аналогічні операції, як і в попередньому – перевіряємо, чи S в сумі із часом переливання відразу в кінцеву посудину менший за R (час переливання з першої в кінцеву посудину): S + 5 = 4 + 5 = 9, 9-ть менше R (9<10), тому алгоритм закінчується, а пройдені стовпці відповідно і є тим шуканим найкоротшим шляхом. Схематично рух по таблиці зображено на рисунку 1.7.

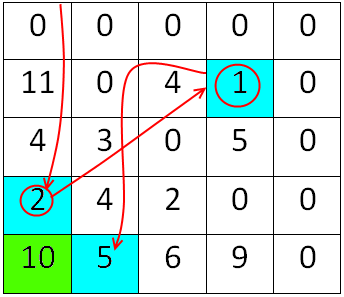
Рисунок 1.7 – Результат проходу таблиці

Порядок проходження стовпців, а відповідно й елементів, запам’ятовується. На основі цих даних на формі будуватиметься шлях проходження у вигляді лінії що з’єднуватиме відповідні елементи поступово по виконанню алгоритму.