2. Изучение электростатического поля

Цель работы: экспериментальное исследование электростатического поля методом электростатической ванны и описание его при помощи силовых линий и поверхностей равного потенциала.

Принадлежности: специальная установка, набор сменных электродов

2.1. Теоретические сведения

2.1.1. Закон Кулона. Напряженность электрического поля

Взаимодействие точечных зарядов q₁и q₂ описывает экспериментальный закон Кулона:

, (2.1)

где - сила, действующая на q₁ со стороны q₂;

r₁₂ - расстояние между зарядами;

- единичный вектор направленный от q₂ к q₁;

_о - диэлектрическая постоянная, определяемая из опыта;

 - диэлектрическая проницаемость среды (для вакуума=1, для диэлектриков>1).

Опыт показывает, что при наличии зарядов q₁, q₂, q₃,..., результирующая сила , действующая со стороны поля на заряд q₁, равна векторной сумме сил , приложенных к нему со стороны каждого из зарядов q_i:

, (2.2)

где ,... определяются по закону Кулона (2.1).

Напряженность электрического поля в данной точке есть векторная величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

, (2.3)

где - сила, действующая на пробный заряд q_о, помещенный в рассматриваемую точку пространства. В частности, напряженность поля точечного заряда q определяется в соответствии с законом Кулона (2.1) по формуле:

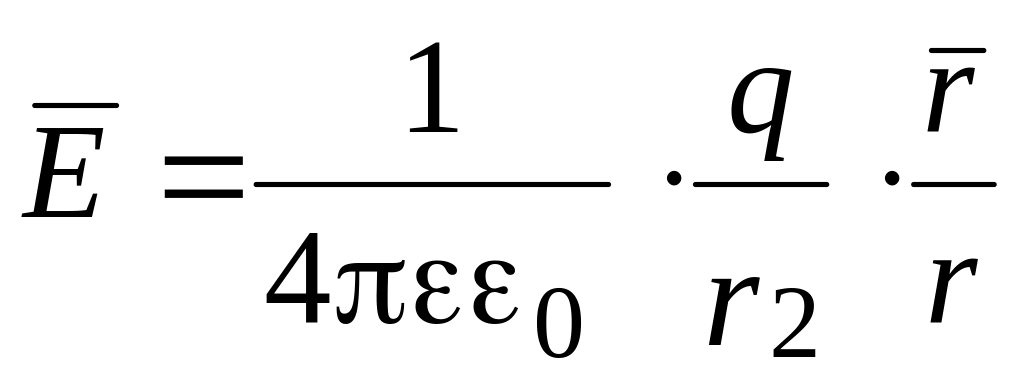, (2.4)

где - вектор, проведенный от точечного заряда q в данную точку.

Поле, создаваемое неподвижными относительно выбранной системы отсчета зарядами, называется электростатическим.

Если поле создается точечными зарядами q₁, q₂,..., то согласно выражению (2.2) имеет место принцип суперпозиции полей:

, (2.5)

где ,... - напряженность полей, создаваемых в данной точке каждым из зарядов q₁, q₂,... в отдельности, а Е - суммарная напряженность результирующего поля.

2.1.2. Работа в электростатическом поле. Потенциал

На заряд q_о в электростатическом поле Е действует сила F = q_оЕ, и, следовательно, при его перемещении совершается работа. Рассмотрим электростатическое поле, создаваемое точечным зарядом q, и найдем работу, совершаемую (силами поля) при перемещении заряда q_о из точки 1 в точку 2 (рис.2.1). Для определенности возьмем заряды q и q_о одного знака. На элементарном участке пути dl совершается работа

Рис.2.1

и , (2.6) где потенциал φ в точке электростатического поля определяется точечным зарядом q и расстоянием r от него до точки: (2.7)

Таким образом, работа по перемещению заряда q_о в поле неподвижного точечного заряда q не зависит от выбора траектории и определяется только его начальным и конечным положением. В частности, работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому контуру L, равна нулю, т.е.

Так как q_о ≠ 0, то . (2.8)

Величину называют циркуляцией вектора Е по замкнутому контуру L . Согласно формуле (2.8) для электростатического (!) поля точечного заряда характерным является то, что в нем циркуляция Е по любому замкнутому контуру равна нулю (электростатическое поле потенциальное, а электростатические силы консервативные).

Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу А₁₂ можно представить как разность потенциальных энергий, которыми обладает заряд q_о в начальной и конечной точках поля заряда q:

А₁₂ = W₁ - W₂. (2.9)

Принято говорить просто об энергии заряда q_о в электростатическом поле. Сравнивая выражения (2.9) и (2.6), получаем

φ(r) = W/q_о. (2.10)

В силу принципа суперпозиции формулы (2.8) - (2.10) остаются справедливыми и в случае, когда электростатическое поле создается зарядами q₁, q₂,... . При этом Е = E₁+ E₂+ ... и φ =φ₁+ φ₂+ ... в каждой точке.

Величину φ называют потенциалом поля в данной точке. Согласно выражению (2.10) потенциал в точке электростатического поля равен потенциальной энергии, которую имел бы единичный положительный заряд, помещенный в эту точку . В частности, потенциал поля точечного заряда определяется формулой (2.7). Из выражения (2.10) получаем единицу потенциала : 1В = 1Дж /1Кл. Для разности потенциалов в точках 1 и 2 имеем:

(2.11)

Таким образом, разность потенциалов в двух точках равна работе, совершаемой полем при перемещении единичного положительного заряда из начальной точки в конечную.

Работа сил поля при перемещении заряда q_о из точки 1 в точку 2 может быть записана также в виде

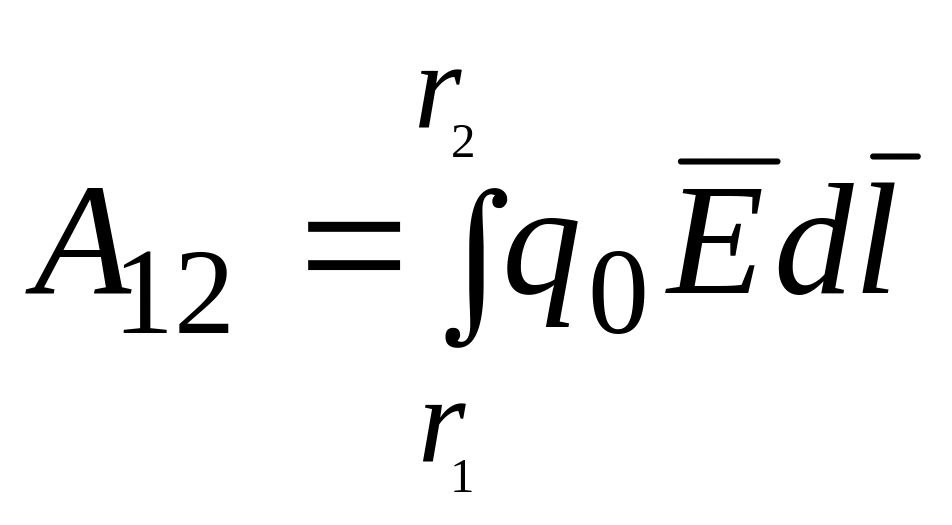(2.12)

Из формул (2.11) и (2.12) вытекает выражение для разности потенциалов:

, (2.13)

где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки.