Выполнение работы:

2.2. Построение оптимального неравномерного двоичного кода методом Шеннона -Фано.

Алгоритм построения двоичного кода Шеннона-Фано

п.1. Буквы располагаются в порядке убывания вероятностей.

п.2. Буквы разделяются на две группы так, чтобы суммы вероятностей букв в каждой группе были по возможности одинаковыми.

п.3. Всем буквам первой группы присваивается очередной кодовый символ «0», а остальным буквам – символ «1».

п.4. Для каждой из групп повторяются пункты 2 и 3 с целью получения кодового слова до тех пор, пока в каждой группе останется одна буква.

Реализуем алгоритм построения кода Шеннона-Фано по пунктам.

1) множество сообщений располагают в порядке убывания вероятностей:

А10 0.2

А9 0.17

А7 0.14

А8 0.1

А1 0.09

А11 0.08

А6 0.06

А4 0.05

А2 0.04

А3 0.03

А5 0.03

А12 0.01

2) Разобьем множество букв на две группы:

• первая группа – (a₁₀, a₉, a₇) с суммарной вероятностью

p(a₁₀)+p(a₉)+p(a₇) = 0.2+ 0.17+ 0.14 = 0.51;

• вторая группа – (a₁, a₂, a₃, a₄, a_5, а_6, а₈,а₁₁,а₁₂) с суммарной вероятностью

p(a₁)+p(a₂)+p(a₃) +p(a₄)+p(a₅) + р(а₆)+ р(а₈)+ р(а₁₁)+ р(а₁₂) = 0.17 + 0.14 + 0.08 + 0.05 + 0.03 + 0.03 = 0.5.

3) Первым символам кодовых слов букв a₁₀, a₉, a₇ присваиваем символ «0», а первым символам кодовых слов букв a₁, a₂, a₃, a₄, a_5, а_6, а₈,а₁₁,а₁₂) присваиваем символ «1».

4) Повторяется п.2 для первой группы, которая разбивается на две подгруппы: (a₁₀) и (a₉, a₇). В соответствии с п.3 вторым символам буквы a₁₀ присваивается символ «0», а символам букв а₉,а₇ присваивается символ «1».

Аналогично проводится кодирование остальных символов букв. Результаты приведены в таблице 2.

0.51 0.49

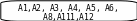0 1

1

0.2 0.31 0.21 0.25

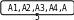
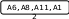0 1 0 1

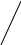
0.13 1 0.11

0.14 0.17 0 0.14 0.11

0.06 0.05

0 1

0 1

0.09 0.04

0 1 0.03 0.03

0 1

0 1

0.1 0.01

0.06 0.08

0 1

0

1

Таблица 2.

Буква	Вероятность	Кодовое слово	Число символов n
A1	0.09	1000	4
A2	0.04	1001	4
A3	0.03	1010	4
A4	0.05	1011	4
A5	0.03	10101	5
A6	0.06	100	3
A7	0.14	011	3
A8	0.1	1110	4
A9	0.17	010	3
A10	0.2	00	2
A11	0.08	1101	4
A12	0.01	1111	4

- это средняя длина кодового слова – среднее количество символов вторичного алфавита, приходящееся на одну букву вторично алфавита.

Рассчитаем среднюю длину кодового слова для каждого из случаев кодирования по следующей формуле:

, (1)

log₂2(0.09*4+0.04*4+0.03*4+0.05*4+0.03*5+0.06*3+0.14*3+0.1*4+0.17*3+0.2*2+008*4+

001*4) = log₂2 *3.26 = 1*3.26 = 3.26.

Рассчитаем значение энтропии источника H(A):

, (2)

H(A)=-( 0.09* log₂ 0.09+ 0.04* log₂ 0.04+0.03* log₂ 0.03+0.05* log₂ 0.05+0.03* log₂ 0.03 + 0.06* log₂ 0.06 + 0.14* log₂ 0.14 + 0.1* log₂0.1 + 0.17 * log₂0.17+0.2* log₂ 0.2+0.08* log₂0.08 +0.01 * log₂0.01)) = - ( 0.09* (- 3.4739) +0.04 *(- 4.6439)+ 0.03*( -5.0589) + 0.05*( -4.3219)+

+ 0.03* (-5.05890) + 0.06*( -4.0589)+ 0.14* (-2.8365) + 0.1* (-3.3219)+ 0.17*( -2.5564)+ 0.2* (-2.3219)+ 0.08*( -3.6439)+ 0.01* ( -6.6439) =

= - ( 0.3127+0.1858+0.1518+0.2160+0.1518+0.2436+ 0.3971+0.3322+ 0.4346+ 0.4644+0.2915+0.0664)) = 3.2479 (бит/символ).

Коэффициент относительной эффективности показывает на сколько используется статистическая избыточность передаваемого сообщения.

Найдем коэффициент относительной эффективности по следующей формуле:

, (3)

Найдем коэффициент статистического сжатия. Коэффициент статистического сжатия характеризует уменьшение количества двоичных знаков на символ сообщения.

, (4)

В формуле (4) числитель max(H(A)) можно записать как

, (5)

n =12.

.