13) Угод между векторами.Условие парал-ти и перрпенд-ти 2-х векторов.
Угол между векторами — угол между направлениями этих векторов
По
определению, угол
между двумя векторами находится в
промежутке [0°;
180°].
Угол
между векторами 
обозначается
так: 
.
Если
векторы перпендикулярны, то угол между
ними равен 90º.
Если векторы сонаправлены, в частности
один из них или оба нулевые, то угол
между ними равен 0о.
Если противоположно направленные
векторы, то угол между ними равен 180º.
Угол
между двумя ненулевыми векторами
находится с помощью вычисления скалярного
произведения.
По определению скалярное
произведение равно произведению длин
векторов на косинус угла между ними
,где векторы и заданы проекциями на координатные оси
Условия
параллельности и перпендикулярности
векторов
Так как скалярное произведение двух
перпендикулярных векторов 
и 
равно
0, то условием перпендикулярности
отличных от нуля векторов будет
равенство 
.
При умножении вектора 
на
скаляр 
получаем
вектор 
одного
направления с 
при
λ > 0и противоположного направления
при λ < 0. Но всегда векторы 
будут
параллельны.
Поэтому
условием параллельности векторов
будет
пропорциональность их соответствующих
координат: 
.
14) Определение и геометрический смысл смешанного произведения 3-х векторов.
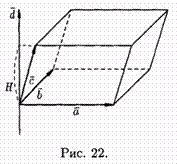
Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb )•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется смешанным.
Выясним геометрический смысл выражения (ахb )*с. Построим параллелепипед, ребрами которого являются векторы а, b , с и вектор d =ахb
Имеем: (а х b) • с = d • с = |d| • прdс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb )*c =S *(±H ), т. е. (axb )*c =±V , где V — объем параллелепипеда, образованного векторами а, b и с.
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
(Не знаю пригодится ли: Свойства смешанного произведения
Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с ха)•b .
Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb)•с=а*(bx с).
Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc=-bac , abc =-cba .
.Смешанное произведение ненулевых векторов а, b и сравно нулю огда и только тогда, когда они компланарны.)
15)Общее уравнение плоскости.Нормальный вектор плоскости.
Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0
где 
-
нормальный вектор плоскости.
В
векторном виде 
.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz