Теория одиночного снимка (лек2)

1. Основные элементы центральной проекции кадрового снимка (в2)

Топографический план (карта) представляют собой ортогональную проекцию точек местности на горизонтальную плоскость (поверхность принятого сфероида) и характеризуется двумя основными свойствами:

1. расстояния в плане пропорциональны соответствующим горизонтальным расстояниям на местности;

2. углы в любой точке плана равны соответствующим горизонтальным углам на местности.

P Допустим, что из точки и S получили

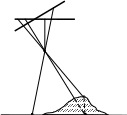
b b₀ a горизонтальный снимок P⁰. Построим

o P⁰ изображение точки местности на

f снимке P⁰. Из рис.5 видно, что снимок

S нельзя считать ортогональной

проекцией точек на местности, так как

проектирующие лучи, с помощью

которых он получается, не

B параллельны друг другу, а

h пересекаются в одной точке - S.

A₀ B₀ E Проекция объекта, полученная в

Рис. 5 результате пересечения плоскости P⁰ с проектирующими лучами, пересекающимися в одной точке, называется центральной проекцией, а точка пересечения этих лучей – центром проекции (точкой фотографирования).

При центральном проектировании различают негативное (обратное) и позитивное (прямое) изображения (рис.6).

Рис. 6

Позитив P получают в случае, когда объект и плоскость проекции расположены по одну сторону от центра проекции S, а негатив N – в в случае когда объект и плоскость проекции расположены по разные стороны от центра проекции S.

Негатив и позитив располагаются симметрично по разные стороны от центра проекции S. Если негатив развернуть на 180^о вокруг оси, проходящей через центр проекции S параллельно плоскостям негатива и позитива, а затем развернуть вокруг оси, лежащей в плоскости позитива и перпендикулярной оси первого разворота, то все точки негатива совпадут с точками позитива. Поэтому при анализе снимка можно рассматривать как негатив, так и позитив. В дальнейшем чаще будем рассматривать позитив, который, как и негатив, будем называть снимком.

При центральном проектировании взаимное плановое положение точек (например А-В на рис.5) на снимке будет нарушено (ab вместо ab₀), так как точка В расположена вне плоскости Е.

Практически получить горизонтальный снимок P⁰ – нельзя. При съемке мы получаем наклонный снимок P. Это в еще большей степени исказит взаимное плановое положение изобразившихся на снимке точках местности. Из рисунка 5 видно, что только изображение плоской местности на горизонтальном снимке соответствует ортогональной проекции.

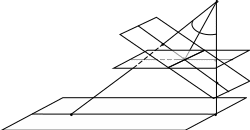
А так как в дальнейшем мы будем рассматривать способы создания топографических карт по фотоснимкам, необходимо рассмотреть основные элементы (точки и линии) центральной проекции(Рис.7) и их свойства.

P- плоскость наклонного снимка, картинная плоскость.

E- горизонтальная (предметная) плоскость.

P⁰ – плоскость горизонтального снимка, параллельная предметной плоскости.

S – центр проекции, в котором сходятся оптические проектирующие лучи. Из него получены наклонный P и горизонтальный снимки P⁰.

SO – главный оптический луч наклонного снимка, перпендикуляр к плоскости P.

o – главная точка наклонного снимка, точка пересечения главным оптическим лучом SO плоскости P.

So=f – фокусное расстояние наклонного снимка.

SN=H – отвесная линия, перпендикуляр к плоскости Е, высота фотографирования.

n – точка надира на наклонном снимке, точка пересечения этого снимка отвесной линией SN. В точке надира сходятся изображения линий, перпендикулярных плоскости Е ( например, изображения деревьев, столбов, углов зданий). Расстояние этой точки от главной точки on= -f tgα₀.

Угол oSn=α₀ – угол наклона снимка Р, определяет отклонение главного оптического луча SO от отвесной линии SN .

S

f

α f

P

o

c n⁰

P⁰

H

n

O

E N

Рис.7