
- •Глава 1. Элементы математической логики и теории
- •Глава 2. Элементы линейной алгебры
- •Глава 3. Векторная алгебра
- •Глава 4. Аналитическая геометрия на плоскости
- •Глава 5. Аналитическая геометрия в пространстве
- •Глава 1. Элементы математической логики и теории множеств
- •1.1. Аксиоматический метод
- •1.2. Алгебра высказываний
- •1.3. Логика предикатов
- •1.4. Множества и их элементы
- •1.5. Операции над множествами
- •1.6. Отображения множеств
- •1.7. Мощность множества
- •Глава 2. Элементы линейной алгебры
- •2.1. Системы линейных уравнений
- •2.2. Матрицы и действия над ними
- •2.3. Запись систем в матричной форме и их решение
- •2.4. Определители и их свойства
- •2.5. Правило Крамера
- •2.6. Решение системы линейных уравнений с неизвестными методом Гаусса
- •2.7. Теорема Кронекера-Капелли
- •2.8. Обратная матрица
- •2.9. Векторное пространство
- •Глава 3. Векторная алгебра
- •3.1. Система координат на прямой, на плоскости и в пространстве
- •3.2. Векторы и линейные операции над ними
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение двух векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия на плоскости
- •4.1. Уравнение линии в заданной системе координат
- •4.2. Различные формы уравнения прямой на плоскости
- •4.3. Основные задачи на прямую на плоскости
- •4.4. Окружность
- •4.5. Эллипс
- •4.6. Гипербола
- •4.7. Парабола
- •4.8. Классификация кривых второго порядка
- •4.9. Построение эллипса, гиперболы, параболы
- •4.10. Кривые второй степени и конические сечения
- •Глава 5. Аналитическая геометрия в пространстве
- •5.1. Поверхности и линии в пространстве
- •5.2. Уравнение плоскости в пространстве
- •5.3. Основные задачи о положении плоскости
- •5.4. Уравнения прямой в пространстве
- •5.5. Основные задачи о положении прямой
- •5.6. Задачи на взаимное расположение прямой и плоскости
- •5.7. Цилиндрические и конические поверхности
- •5.8. Поверхности вращения
- •5.9. Технические приложения геометрических свойств поверхности
5.7. Цилиндрические и конические поверхности
Займемся
теперь изучением поверхностей. Их
уравнения после преобразований могут
быть приведены к виду
 ,
Мы будем предполагать, что
,
Мы будем предполагать, что
 есть многочлен относительно
Степень этого многочлена относительно
определяет порядок
алгебраической поверхности.
Можно показать, что он не зависит от
выбора координатных осей. Ранее мы
убедились в том, что поверхностями 1-го
порядка являются плоскости. Займемся
исследованием поверхностей 2-го порядка.
есть многочлен относительно
Степень этого многочлена относительно
определяет порядок
алгебраической поверхности.
Можно показать, что он не зависит от
выбора координатных осей. Ранее мы
убедились в том, что поверхностями 1-го
порядка являются плоскости. Займемся
исследованием поверхностей 2-го порядка.
Начнем с цилиндрической поверхности. Цилиндрической называется поверхность, образованная прямыми, называемыми образующими, параллельными некоторой данной прямой и пересекающими данную линию , которая называется направляющей. Пусть направляющая цилиндрической поверхности определяется уравнениями
 (5.31)
(5.31)
а образующие уравнениями
 (5.32)
(5.32)
где
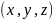 есть точка, принадлежащая направляющей,
а
- текущие координаты поверхности.
Исключая
есть точка, принадлежащая направляющей,
а
- текущие координаты поверхности.
Исключая
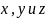 из четырех уравнений (5.31) и (5.32), получим
искомое уравнение цилиндрической
поверхности.
из четырех уравнений (5.31) и (5.32), получим
искомое уравнение цилиндрической
поверхности.
Пример
5.13.
Составить уравнение цилиндрической
поверхности, образующие которой
параллельны прямой
 ,
а направляющей служит прямая
,
а направляющей служит прямая
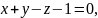
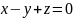 .
Рассмотрим канонические уравнения
образующих:
.
Рассмотрим канонические уравнения
образующих:
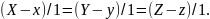
Обозначим
через
величину каждого из этих отношений,
тогда
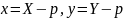 ,
,
 .
Подставляя эти значения
в данные уравнения направляющей,
получим:
.
Подставляя эти значения
в данные уравнения направляющей,
получим:
 .
Исключив
,
найдем:
.
Исключив
,
найдем:
 Это есть уравнение плоскости, проходящей
через данную направляющую и параллельной
прямой
.
Это есть уравнение плоскости, проходящей
через данную направляющую и параллельной
прямой
.
Конической называется поверхность, образованная прямыми (образующими конуса), проходящими через данную точку (вершину конуса) и пересекающими данную линию (направляющую конуса).
Пусть направляющая конуса задается уравнениями
 ,
(5.33)
,
(5.33)
а
вершина конуса имеет координаты
 Канонические
уравнения образующих конуса как прямых,
проходящих через точку
Канонические
уравнения образующих конуса как прямых,
проходящих через точку
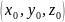 и через точку
и через точку
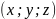 направляющей, будут:
направляющей, будут:
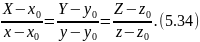
Исключая
 из уравнений (5.33) и (5.34), получим искомое
уравнение конической поверхности.
из уравнений (5.33) и (5.34), получим искомое
уравнение конической поверхности.
Пример 5.14. Составить уравнение конуса с вершиной в начале координат и направляющей
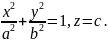
Канонические
уравнения образующих, проходящих через
вершину (0;0;0) конуса и точку
 направляющей, будут:
направляющей, будут:
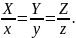 Исключим
из четырех данных уравнений. Заменяя
Исключим
из четырех данных уравнений. Заменяя
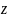 на c, определим
из последних двух уравнений:
на c, определим
из последних двух уравнений:
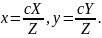
 Подставляя
эти значения
в первое уравнение направляющей, будем
иметь:
Подставляя
эти значения
в первое уравнение направляющей, будем
иметь:
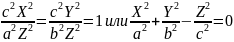
Если в рассмотренном примере , то направляющей будет окружность, и мы получим круговой конус.
5.8. Поверхности вращения
Рассмотрим в плоскости Oyz некоторую линию L, имеющую уравнение F(Y,Z)=0. Найдем уравнение поверхности, полученной от вращения этой линии вокруг оси Oy (рис.5.8).
Возьмем
произвольную точку M(x;y;z) этой поверхности
и проведем через нее плоскость,
перпендикулярную оси вращения Oy.
Очевидно, в пересечении этой плоскости
с нашей поверхностью получится
окружность с центром N на оси вращения.
Координаты точки N будут (0;y;0). Радиус
окружности MN как расстояние между
точками N и M равен
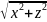 .
С другой стороны, ясно, что этот радиус
является абсолютной величиной аппликаты
той точки
данной линии L, ордината которой есть
y. Следовательно, полагая в данном
уравнении
.
С другой стороны, ясно, что этот радиус
является абсолютной величиной аппликаты
той точки
данной линии L, ордината которой есть
y. Следовательно, полагая в данном
уравнении
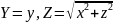
(координаты точки ), мы получим искомое уравнение поверхности вращения:

Таким образом, мы приходим к следующему правилу:
чтобы
получить уравнение поверхности,
образованной вращением линии L, лежащей
в плоскости Oyz, вокруг оси Oy, надо в
уравнении этой линии заменить z на
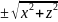 .
.

Рис.5.8. Поверхность вращения.
Аналогичные правила будут иметь место и по отношению к поверхностям, полученным вращением плоских линий вокруг других координатных осей.
Уравнение поверхности, полученной вращением эллипса

вокруг оси Oz, будет
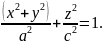
Это
уравнение определяет поверхность,
называемую эллипсоидом
вращения.
Пересекая этот эллипсоид плоскостью
 ),
параллельной плоскости Oxy, получим в
сечении окружность, уравнения которой
будут:
),
параллельной плоскости Oxy, получим в
сечении окружность, уравнения которой
будут:
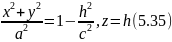
и
радиус которой равен
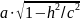 .
.
Следовательно,
при изменении
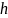 от
значения
от
значения
 до значения
до значения
 окружность (5.35) описывает эллипсоид
вращения.
окружность (5.35) описывает эллипсоид
вращения.
Возьмем теперь вместо окружности (5.35) эллипс
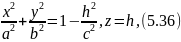
лежащий
в плоскости
 ,
параллельной плоскости xOy, полуоси
,
параллельной плоскости xOy, полуоси
которого
равны
и
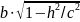 .
При изменении
.
При изменении
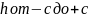 этот эллипс описывает поверхность,
уравнение которой получим, исключив
из уравнений (5.36):
этот эллипс описывает поверхность,
уравнение которой получим, исключив
из уравнений (5.36):

или
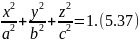
.
Поверхность,
определяемая уравнением (5.37) называется
эллипсоидом,
а величины
 - его полуосями
(рис.5.9).
- его полуосями
(рис.5.9).
Пересекая
эллипсоид координатными плоскостями
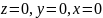 ,
получим в сечении эллипсы:
,
получим в сечении эллипсы:
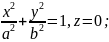


Не
умаляя общности, мы можем считать, что
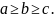 Если
Если
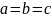 ,
то уравнение (5.37) определяет сферу; если
,
то уравнение (5.37) определяет сферу; если
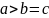 ,
то - удлиненный эллипсоид вращения с
осью вращения
,
то - удлиненный эллипсоид вращения с
осью вращения
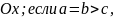 то - сжатый эллипсоид вращения с осью
вращения
.
Если среди чисел
нет равных, то эллипсоид называется
трехосным.
то - сжатый эллипсоид вращения с осью
вращения
.
Если среди чисел
нет равных, то эллипсоид называется
трехосным.

Рис.5.9. Эллипсоид.
Рассмотрим теперь гиперболоиды.
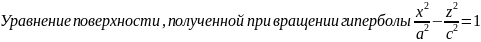
вокруг
оси
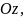 имеет вид:
имеет вид:
 Это уравнение определяет поверхность,
называемую однополостным
гиперболоидом
вращения.
Пересекая ее плоскостью
Это уравнение определяет поверхность,
называемую однополостным
гиперболоидом
вращения.
Пересекая ее плоскостью
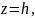 параллельной плоскости
параллельной плоскости
 получим в сечении окружность:
получим в сечении окружность:
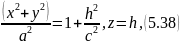
радиус
которой равен


Рис. 5.10. Однополостный гиперболоид.
Следовательно, при изменении от до окружность (5.38) описывает однополостный гиперболоид вращения.
Возьмем теперь вместо окружности (5.38) эллипс:
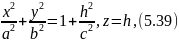
лежащий
в плоскости
,
параллельной плоскости
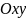 ,
полуоси которого равны
,
полуоси которого равны
 и
и
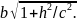 При изменении
от
до
При изменении
от
до
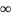 этот эллипс описывает поверхность
(рис.5.10), уравнение которой получим,
исключив
из уравнений (5.39):
этот эллипс описывает поверхность
(рис.5.10), уравнение которой получим,
исключив
из уравнений (5.39):

Поверхность, задаваемая уравнением (5.40), называется однополостным гиперболоидом, а величины - его полуосями.
Вращая гиперболу
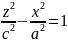
вокруг
оси Oz, мы получим двуполостный
гиперболоид.
Его уравнение будет
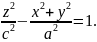
Пересекая
его плоскостью
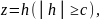 перпендикулярной к оси вращения Oz,
получим в сечении окружность
перпендикулярной к оси вращения Oz,
получим в сечении окружность

радиус
которой равен
 .
При изменении
.
При изменении
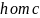 до
окружность (5.41) описывает одну полость
гиперболоида, а при изменении
до
окружность (5.41) описывает одну полость
гиперболоида, а при изменении
 до
- другую его полость.
до
- другую его полость.
Возьмем вместо окружности (5.41) эллипс
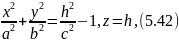
лежащий
в плоскости
параллельной плоскости xOy, полуоси
которого равны
и
 .
При изменении
.
При изменении
 этот
эллипс описывает двуполостную поверхность,
уравнение которой получим, исключая
из уравнений (5.42):
этот
эллипс описывает двуполостную поверхность,
уравнение которой получим, исключая
из уравнений (5.42):
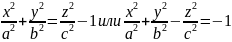
Поверхность второго порядка, описываемая этим уравнением называется двуполостным гиперболоидом, а величины - его полуосями.
Параболоид
вращения получается вращением
параболы
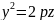 вокруг оси Oz. Его уравнение будет
вокруг оси Oz. Его уравнение будет
 (5.43)
(5.43)
В
сечении его плоскостью
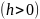 ,
перпендикулярной оси вращения
,
перпендикулярной оси вращения
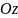 ,
получается окружность, уравнения которой
будут
,
получается окружность, уравнения которой
будут
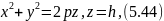
ее
радиус равен  .
Следовательно, при изменении
от
до-окружность
.
Следовательно, при изменении
от
до-окружность
 описывает параболоид вращения.
описывает параболоид вращения.
Возьмем вместо окружности эллипс
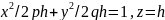 (5.45)
(5.45)
Здесь
 - положительные числа. Полуоси этого
эллипса равны
- положительные числа. Полуоси этого
эллипса равны
 .
При изменении
от
до
этот эллипс описывает поверхность,
называемую эллиптическим параболоидом,
уравнение которого получается
исключением
из уравнений
.
При изменении
от
до
этот эллипс описывает поверхность,
называемую эллиптическим параболоидом,
уравнение которого получается
исключением
из уравнений
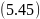 :
:
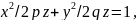
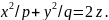 (5.46)
(5.46)
Простейшее
уравнение гиперболического
параболоида
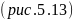 имеет вид:
имеет вид:
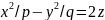 ,
,
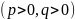 ,
,
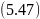
т.е.
отличается от уравнения
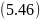 только
знаком при
.
Плоскость координат пересекает эту
поверхность по параболе
только
знаком при
.
Плоскость координат пересекает эту
поверхность по параболе


для
которой ось
является осью симметрии и которая
расположена в положительном направлении
оси
.
Плоскость
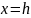 ,
параллельная плоскости
,
параллельная плоскости
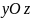 ,
пересекает поверхность
по параболе, уравнения которой будут:
,
пересекает поверхность
по параболе, уравнения которой будут:
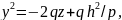 x=h
или
x=h
или
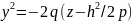 ,
(5.49)
,
(5.49)
Из
этих уравнений видно, что эти параболы,
расположенные в плоскостях
,
имеют один и тот же параметр, их оси
симметрии находятся в плоскости
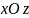 и параллельны оси
,
ветви парабол направлены вниз (в
отрицательном направлении оси
),
а их вершины имеют координату z=
и параллельны оси
,
ветви парабол направлены вниз (в
отрицательном направлении оси
),
а их вершины имеют координату z= .
Вершины парабол
.
Вершины парабол
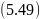 расположены на параболе
.
расположены на параболе
.
Таким
образом, гиперболический параболоид
можно рассматривать как поверхность,
образованную движущейся параболой, ось
симметрии которой остается в плоскости
 ,
а вершина движется по параболе
.
Плоскость параболы остается параллельной
плоскости
,
а вершина движется по параболе
.
Плоскость параболы остается параллельной
плоскости
 .
.
Пересекая
гиперболический параболоид
плоскостью
,
получим в сечении гиперболу,
уравнения которой:
 ,
.
При
,
.
При
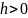 действительная ось симметрии гиперболы
будет параллельна оси
,
при
действительная ось симметрии гиперболы
будет параллельна оси
,
при
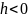 - оси
.
- оси
.
Так
как уравнение (5.47) содержит только
квадраты координат
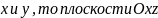 и
являются
плоскостями симметрии для поверхности.
и
являются
плоскостями симметрии для поверхности.
Среди поверхностей второго порядка упомянем еще конус с вершиной в начале координат, направляющей линией которого является эллипс, и цилиндры, направляющие линии которых, лежащие в плоскости Oxy являются эллипсами, гиперболами, параболами.
