Занятие 7. Графики функций (продолжение). Решение уравнений методом подбора параметра.

В Excel существует возможность решать уравнения практически любой сложности. Делается это методом подбора параметра.

рис. 94

Задание 1.

Постройте график функции y=2x+5 для x[-5;5]. Для заполнения столбца X таблицы воспользуйтесь командой Прогрессия: введите первое значение х = -5, затем на вкладке Главная в группе Редактирование выберите команду Прогрессия, установите переключатель по столбцам, введите в поле Предельное значение число 5 и ОК. Столбец будет заполнен значениями аргумента, Error: Reference source not found.

рис. 95

рис. 96

Постройте график функции.

рис. 97

Теперь решим уравнение 2x+5=0.

На графике видно, что решение существует, но определить точное значение x мы "на глаз" не можем.

В таблице подбираем строку, наиболее близкую к корню уравнения.

Скопируем эту строку таблицы, разместив эти данные на свободном месте (в данном случае – в ячейке D1).

В ыделяем ячейку Е1 (т.е. ту, в которой мы хотим, чтобы у был равен 0), выбираем Подбор параметра.

рис. 98

В результате компьютер даёт нам ответ: если y=0, то x=-2,5).

Это - решение уравнения f(x)=0

рис. 99

Активируйте мышью Область построения диаграммы и сделайте на графике соответствующую надпись.

рис. 100

Для этой же функции решим уравнение f(x) = 10

С нова находим строку, близкую по значению х к числу 10, и копируем её в свободные ячейки:

рис. 101

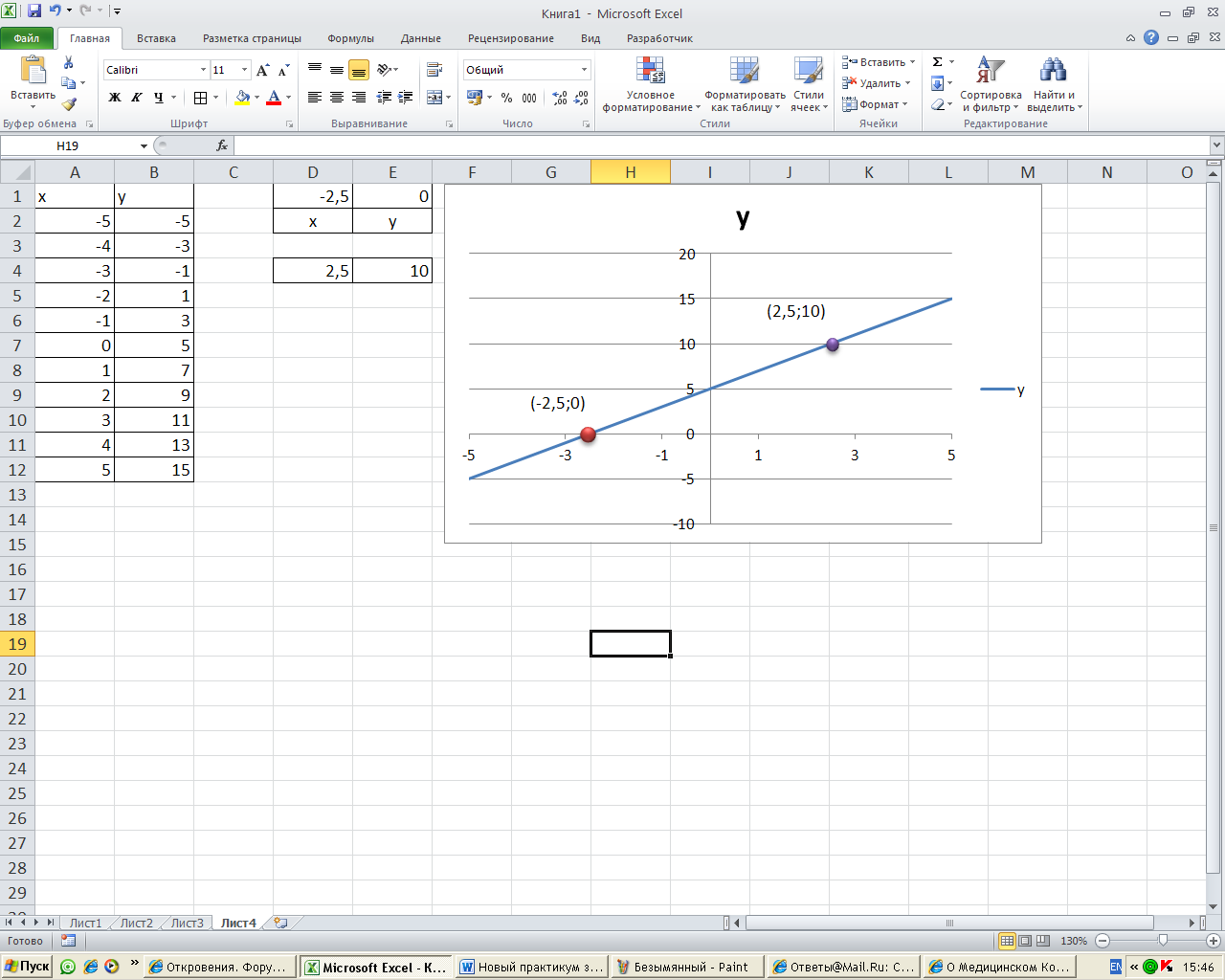Рис. 102

Задание 2.

Решим квадратное уравнение 5x²+10x-30=0.

Для начала построим график: по нему видим, что уравнение имеет два корня.

С помощью подбора параметра эти корни можно легко найти. Здесь возникает проблема: компьютер выдаёт только одно решение. Причём будет найден тот корень, значение которого ближе к тому значению, которое мы выбирали для подбора параметра. Поэтому выход такой: скопировать из таблицы две строки, в которых значения наиболее близки к искомым корням, и дать команду подбора параметра два раза.

рис. 103

Найдите корни уравнения и сделайте надписи на графике.

Задание 3.

Постройте график функции y=x³-5.

Р ассчитайте координаты указанных точек. Подпишите точки.

Рис. 104

Занятие 8. Решение задач на подбор параметра.

Задание 1. Выяснить экономическую целесообразность работы контролёра в общественном транспорте.

Определим, сколько безбилетников в сутки должны приобрести билеты, чтобы окупилась зарплата контролёра.

Предположим, мы хотим установить зарплату контролёра25 000 рублей. Также для начала введём количество безбилетников – 5

Создайте таблицу по образцу:

В ячейку С5 введена формула, в которой С2/24 – это средняя заработная плата контролёра в сутки, так как число рабочих дней в месяце обычно составляет 24.

рис. 105

Для того, чтобы работа контролёра стала не убыточной для автопредприятия, разность между суммой полученных штрафов и зарплатой должна быть больше или равна 0. Эта разность вычисляется в ячейке С4.

Выделите ячейку С4, включите подбор параметра и получите искомое количество безбилетников: 5.

рис. 106

рис. 107

Таким образом, контролёр должен оштрафовать в день как минимум одного безбилетника, а иногда и двоих, чтобы оправдать свою зарплату.

Задание 2. Правительство Москвы решило уменьшить размер штрафа до 500руб. Сколько безбилетников надо будет оштрафовать при таком размере штрафа?

рис. 108

Задание 3. Пусть размер штрафа всё же останется 1000 руб. Сколько человек надо будет оштрафовать, чтобы контролёр смог получать зарплату 35 000 руб.?

рис. 109

Задание 4. Какой должен быть размер штрафа для оправдания работы контролёра с зарплатой в 35 000 рублей, если известно, что в день он штрафует 10 человек?

рис. 110

рис. 111

Задание 5. Что выгоднее: ездить во МГАДА на автобусе или на личном автомобиле?

Для начала будем считать, что расстояние от места проживания студента до академии составляет 10 км, то есть туда и обратно в сумме необходимо проехать 20 км.

В ячейке B4 число 0,08 означает, что средний расход бензина на каждый 1км пробега составляет 0,08л, следовательно, цену бензина надо умножать на коэффициент 0,08 (

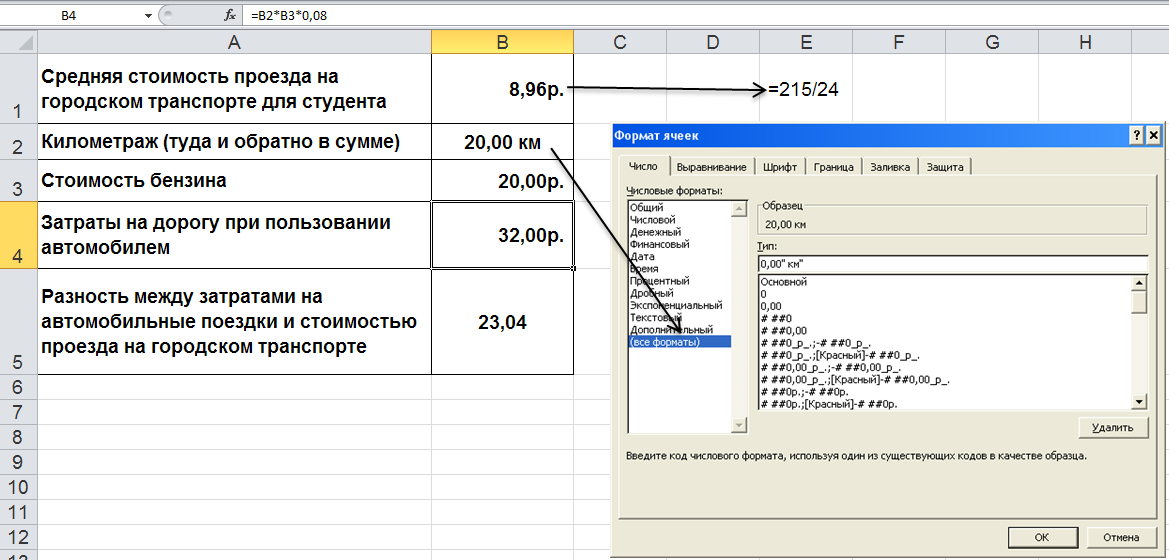рис. 112

На каком расстоянии от МГАДА должен жить студент, чтобы ему было выгоднее пользоваться личным автомобилем?

Как и раньше, нам необходимо приравнять к 0 разность между затратами на автомобильные поездки и стоимостью проезда на городском автобусе.

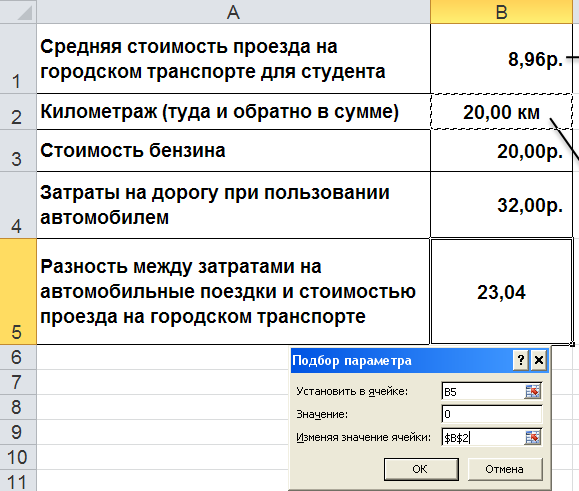рис. 113

Получаем ответ:

рис. 114

Таким образом, если студент живёт на расстоянии ближе, чем 5,6/2=2,8км от академии, то ему будет выгоднее использовать личный автомобиль.