
- •Задача 7 Контрольные карты
- •I Стандартные значения не заданы:
- •II Стандартные значения заданы (т.Е. Заданы , и возможно или ):
- •В зависимости от того заданы ли стандартные значения показателя качества или нет первый этап разбивается на два варианта:
- •I Стандартные значения не заданы:
- •II Стандартные значения заданы (т.Е. Заданы , и возможно ):
- •В зависимости от того заданы ли стандартные значения показателя качества или нет первый этап разбивается на два варианта:
- •I Стандартные значения не заданы:
- •II Стандартные значения заданы (т.Е. Заданы или или ):
Задача 7 Контрольные карты
Контрольные карты (контрольные карты Шухарта) – инструмент, позволяющий отслеживать изменение показателя качества во времени для определения стабильности технологического процесса, а также корректировки процесса для предотвращения выхода показателя качества за допустимые пределы.
Контрольные карты делятся на два вида:
для контроля непрерывных величин:
x - карта контроля измеряемых значений;
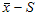 -
карта контроля средних значений и
среднеквадратичных отклонений;
-
карта контроля средних значений и
среднеквадратичных отклонений;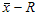 -
карта контроля средних значений и
размахов;
-
карта контроля средних значений и
размахов;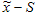 -
карта контроля медиан и среднеквадратичных
отклонений;
-
карта контроля медиан и среднеквадратичных
отклонений; -
карта контроля медиан и размахов;
-
карта контроля медиан и размахов;
для контроля дискретных величин:
p - карта контроля доли неисправных изделий в выборке (применяются как при постоянном, так и при переменном объеме выборки);
np - карта контроля числа неисправных изделий в выборке (применяются только при постоянном объеме выборки);
с - карта контроля числа несоответствий в выборке (применяются только при постоянном объеме выборки);
u - карта контроля числа несоответствий на одно изделие в выборке (применяются как при постоянном, так и при переменном объеме выборки).
Наилучший контроль показателя качества дает использование карт. При использовании вычислительной техники ее построение не вызывает трудностей. При ручном счете легче вычислять медиану и размах измеренных значений показателя качества, поэтому широкое применение нашли и карты. карты практически не применяются, т.к. если есть возможность вычислить среднеквадратичное отклонение, то расчет медианы вместо среднего арифметического объяснить трудно.
Методика построения , , карт:
В зависимости от того заданы ли стандартные значения показателя качества или нет первый этап разбивается на два варианта:
I Стандартные значения не заданы:
Соберите предварительные данные о протекании процесса. Для этого необходимо провести измерения показателя качества в нескольких подгруппах (например, измерения в нескольких партиях изделий).
В зависимости от выбранного типа карты вычислите необходимые статистические показатели
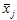 или
или
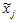 ,
,
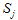 или
или
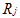 для
каждой подгруппы полученных значений
по формулам:
для
каждой подгруппы полученных значений
по формулам:
![]() -
среднеарифметическое значение показателя
качества в подгруппе;
-
среднеарифметическое значение показателя
качества в подгруппе;
- медиана подгруппы. Вычисляется следующим образом:
расположите измеренные значения в порядке возрастания или убывания;
если количество измеренных значений нечетное, то медиана равна значению, которое располагается в середине ряда. Если количество измеренных значений четное, то медиана равна среднему арифметическому двух значений, расположенных в середине ряда;
![]() -
среднеквадратичное отклонение показателя
качества в подгруппе;
-
среднеквадратичное отклонение показателя
качества в подгруппе;
![]() -
размах показателя качества в подгруппе,
-
размах показателя качества в подгруппе,
где i – индекс измеренного показателя качества в подгруппе;
j – индекс подгруппы;
n - количество изделий в подгруппе;
![]() –
максимальное
значение в подгруппе,
–
максимальное
значение в подгруппе,
![]() –
минимальное
значение в подгруппе.
–
минимальное
значение в подгруппе.
Рассчитайте среднеарифметические значения вычисленных на предыдущем шаге статистических показателей
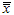 или
или
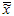 ,
,
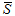 или
или
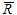 по
формулам:
по
формулам:
![]() -
среднеарифметическое средних значений
подгрупп;
-
среднеарифметическое средних значений
подгрупп;
![]() -
среднеарифметическое медиан подгрупп;
-
среднеарифметическое медиан подгрупп;
![]() -
среднеарифметическое значение
среднеквадратичных отклонений подгрупп;
-
среднеарифметическое значение
среднеквадратичных отклонений подгрупп;
![]() -
среднеарифметическое размахов подгрупп;
где k
– количество подгрупп.
-
среднеарифметическое размахов подгрупп;
где k
– количество подгрупп.
При
использовании метода медиан можно
определить вместо
![]() ,
а вместо
,
а вместо
![]() .
.
Вычислите значения для центральной линии, нижнего и верхнего контрольного пределов
для
![]() карты:
карты:
![]()
![]() или
или
![]()
![]() или
или
![]()
для
![]() карты:
карты:
![]()
![]()
![]()
для R карты:
![]()
![]()
![]()
для S карты:
![]()
![]()
![]()
Все коэффициенты определяются в соответствии с таблицей, приведенной ниже.
