3.3.4. Динамическая идентификация

Многие технологические объекты управления, функционирование которых в динамике еще недостаточно изучено, не могут быть описаны аналитически. Для получения их динамических моделей также применяются экспериментальные методы. Целью последних является нахождение аналитических выражений, описывающих динамику объекта управления с требуемой степенью точности. В отличие от статических моделей динамические связывают выходную величину с входным воздействием в процессе их изменения во времени.

В практике предшествующих дисциплин для записи динамических моделей линейных систем использовался аппарат дифференциальных уравнений. Как правило, технологические объекты управления являются системами, элементы которых имеют нелинейные характеристики и описываются уравнениями высоких порядков.

В передаточных устройствах электропривода имеются люфты, возможно наличие сухого трения, приходится учитывать упругости их элементов и т.д.

Применение методов математического моделирования избавляет исследователя от решения дифференциальных уравнений, но при этом необходимо иметь аналитические модели всех звеньев.

Экспериментальные методы позволяют получить формальную модель практически любого объекта по результатам обработки экспериментальных данных. Существуют активные и пассивные эксперименты.

Активный эксперимент основан на задании объекту специально сформированных управляющих или возмущающих воздействий. По реакции объекта на эти воздействия устанавливаются и оцениваются его динамические свойства. Обычно изучается реакция на скачкообразные, гармонические или импульсные воздействия. Полученные переходные или частотные характеристики позволяют определить, например, для линейной системы передаточные коэффициенты, постоянные времени отдельных звеньев и динамические свойства объекта в целом.

Не для всех систем может быть поставлен активный эксперимент. Иногда он может быть неприемлем из-за дороговизны специального дополнительного оборудования, высокой стоимости его монтажа, нередко его реализация невозможна по условиям техники безопасности. В этих случаях применяется пассивный эксперимент. Сущность его заключается в фиксации значений входных и выходных переменных в нормальных эксплуатационных динамических режимах.

Одним из сравнительно несложных современных методов динамической идентификации, основанных на результатах пассивного эксперимента, является метод Калмана. Сущность его заключается в следующем:

• в процессе эксплуатации через строго фиксированные интервалы времени записывают значения входных и выходных параметров;

• выбирают наиболее простой вид аналитической модели, записанной в виде разностного уравнения того или иного порядка;

• по результатам эксперимента и принятого типа модели методом минимума суммы квадратов отклонений определяют коэффициенты разностного уравнения;

• решают разностное уравнение и сравнивают полученные динамические характеристики с экспериментом;

• при больших отклонениях задаются разностным уравнением более высокого порядка и повторяют расчет.

Сопоставление изложенной выше методики динамической идентификации с порядком выполнения статической идентификации свидетельствует об их аналогии. Отличие состоит лишь в моделях: модель в статике описывается алгебраическим уравнением, динамическая модель — разностным.

Для дифференциального линейного уравнения k-ro порядка аналогом будет разнoстное уравнение вида

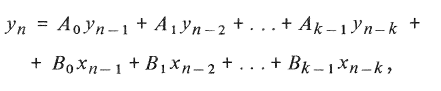
где n — номер точки эксперимента; А, В — коэффициенты разностного уравнения. Оно может быть принято в качестве исходной модели при динамической идентификации.

Поскольку порядок идентифицируемого объекта обычно неизвестен, следует начинать с наиболее простой модели, а именно - разностного уравнения первого порядка вида

Если модель окажется недостаточно адекватной, следует взять в качестве модели разностное уравнение второго порядка

y _n = A ₀ y_{n –1} + A ₁ y_{n –2} + B _o x_{n -1} + B ₁ x_{n -2}

Далее, используя методику минимизации суммы квадратов отклонений, т.е. функционала вида

получаем систему уравнений из которых можно определить коэффициенты

А₀, А_1: В₀, В_}, удовлетворяющие критерию оптимальности.

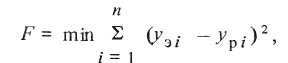
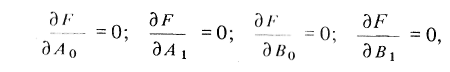
Пример 3.4. Для анализа температурного режима мощного редуктора фиксировалось нарастание температуры масла в картере при приложении номинальной нагрузки. Результаты измерений приведены в табл. 3.6. Требуется определить постоянную нагрева редуктора.

Таблица 3.6. Данные эксперимента

t,ч	0	1	2	3	4	5	6	7	8	9
Θ,o C	12	38,7	54,9	64,8	70,7	74,3	76,6	77,9	78,7	80
Θмод,oC	-	-	54,916	-	70,7	-	-	-	78,66	-

Из данных эксперимента видно, что температура изменилась от Θ _нач = 12 °С до Θ _уст = 80 °С. Для идентификации используем разностное уравнение первого порядка

Θ _n = A ₀Θ _{n –1} + B ₀ Θ _уст .

Для упрощения расчетов примем интервал времени измерений замеров Δt =2 ч.

Для минимизации суммы квадратов отклонений запишем функционал

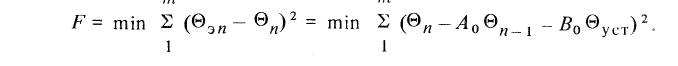
Приравнивая нулю частные производные от функционала

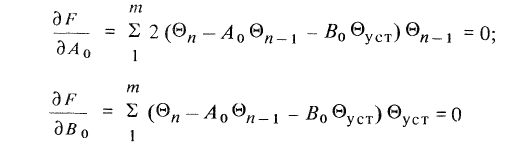
и с учетом того, что

и Θ_уст ≠ 0,

получим систему канонических уравнений

где m - число экспериментальных точек.

Так как интервал времени принят равным 2 ч., то из полученных экспериментальных данных при m = 4 выбираем точки:

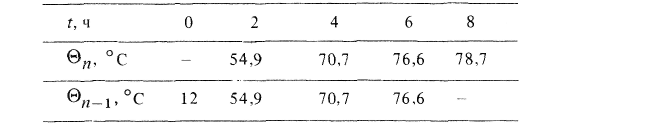
Таблица 3.7. Расчетные точки

Тогда

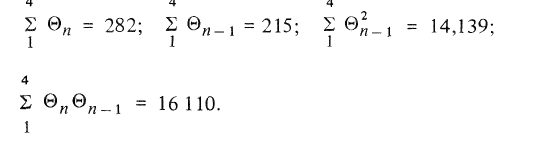
Подставляя полученные значения в выражения для А₀ и В₀, получаем

А₀ = 0,368; В₀ = 0,632, и разностное уравнение при Θ_уст = 80 °С принимает вид

Для проверки адекватности модели по полученному выражению рассчитаны значения Θ при тех же интервалах времени (табл. 3.6).

Сравнивая расчетные данные с данными эксперимента, убеждаемся в хорошей адекватности модели объекту. Это позволяет сделать вывод о возможности описания объекта дифференциальным уравнением первого порядка вида

решением которого является

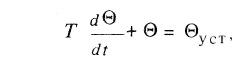
где, полагая Θ = Θ_n , Θ _нач = Θ_n-1 и t = Δ t, при n= 1 получаем

А₀ = e^{-─Δ t /T} ,

откуда

Т = ─ Δn/ln A₀ = ─2/ln 0,368= 2/0,9997= 2ч.

Постоянная нагрева равна 2 ч, и дифференциальное уравнение имеет вид