3.3.2. Идентификация одномерных детерминированных объектов

Задача состоит в представлении в аналитическом виде существующей связи между входом и выходом одномерного объекта. Полагаем, что при эксперименте случайные помехи отсутствуют и в экспериментально снятых значениях нет разброса. Для таких объектов модель наиболее часто описывается полиномом вида

Степень полинома ориентировочно можно определить но разностям экспериментально спитых ординат функции при постоянных приращениях аргумента. Она принимается равной такому порядку разностей, при котором они становятся примерно постоянными во всем диапазоне изменения входной величины. Например, при неизменных разностях между ординатами модель описывается полиномом первой степени, при неизменных разностях между разностями второго порядка - полиномом второй степени и т.д.

Оптимальной может считаться модель, у которой при определенных расчетом коэффициентах сумма квадратов отклонений расчетных y_p и экспериментальных у_э значений будет минимальной, т.е. минимизируется функционал

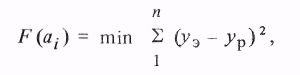(3.15)

где n - число опытов.

Для определения коэффициентов модели составляют систему уравнений типа

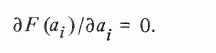(3.16)

Совместное решение полученных уравнений относительно _i дает такие их значения, при которых удовлетворяется условие (3.15).

Для упрощения (3.16) целесообразно начало отсчета абсциссы x_i помещать в середину интервала экспериментально снятых значений и пользоваться симметричными значениями х_i (одинаковыми, но различными по знакам). В этом случае все суммы нечетных степеней х_i будут обращаться в нуль, что существенно упростит систему уравнений.

Например, если в качестве модели выбран полином второй степени

(3.17)

то функционал (3.15) имеет вид

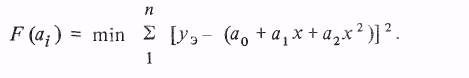
Коэффициенты являются неизвестными переменными.В соответствии с (3.16) составляем систему уравнений

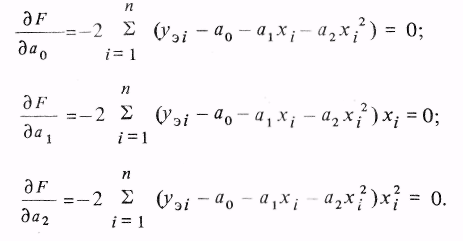
Приравнивая суммы нечетных степеней х_i нулю, получаем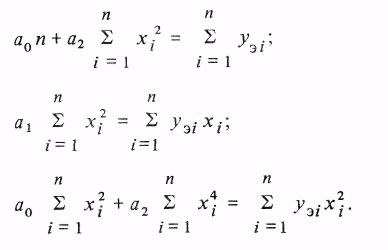

Решение относительно коэффициентов:

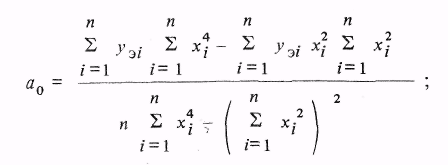(3.18)

.

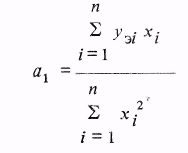
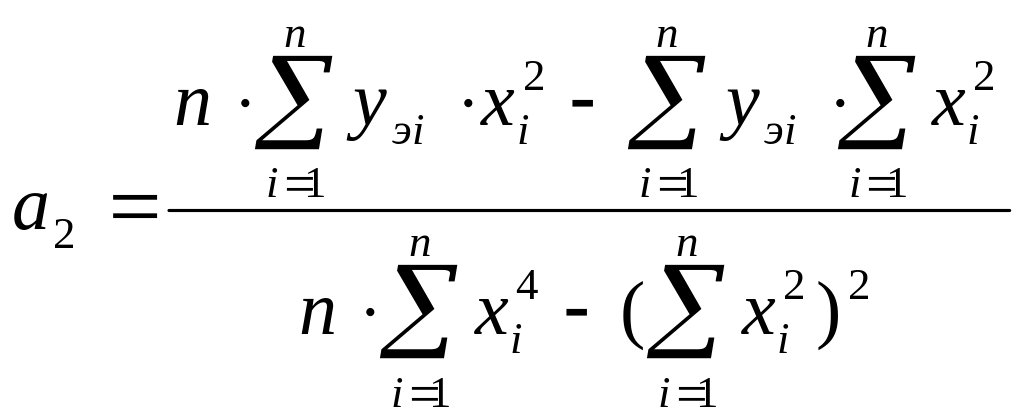Рассчитав коэффициенты и подставив их в (3.17), получим уравнение регрессии.

Пример 3.2. Получить аналитическую зависимость скорости холостого хода двигателя _ХХ от тока возбуждения питающего генератора, если эксперимент дал значения, приведенные в табл. 3.1.

Таблица 3.1. Данные эксперимента

I_В;Э, 10³ А 50 100 150 200 250 300 350 400 450

_ХХ, рад/с 38 65 90 115 133 150 162 172 178

_ХХ, рад/с 36,6 65,5 91,2 113,7 133 149,1 163 171,7 178,2

Двигатель и генератор типа П-21, Р_НОМ = 0,037 кВт, U_НОМ = 220 В,

I_Я.НОМ = 1,61 А, I _В.НОМ = 0,4 А, _НОМ = 152 рад/с

Для облегчения расчетов примем х = I_в/50 и у = _ХХ/100 и перенесем ось у в точку и абсциссой х = +5. Тогда исходные данные примут вид табл. 3.2. Расчеты сумм для (3.18) приведены в табл. 3.3.

Рассчитываем коэффициенты:

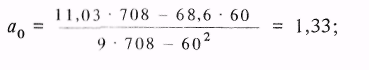
₁ = 10,6/60 = 0,177;

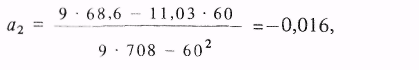
получаем уравнение модели (3.17): у = 1,33 + 177х  016х².

Таблица 3.2. Смещенные данные эксперимента

x_Э -4 -3 -2 1 0 1 2 3 4

у_Э 0,38 0,65 0,9 1,15 1,33 1,5 1,62 1,72 1,78

Таблица 3.3. Расчет сумм

у_Э x_Э x_Э ² x_Э ⁴ у_Э x_Э у_Э x_Э ²

0,38 -4 16 256 -1,52 6,08

0,65 -3 9 81 -1,95 5,85

0,9 -2 4 16 -1,80 3,6

1,15 -1 1 1 -115 1,15

1,33 0 0 0 0 0

1,5 1 1 1 1,50 1,5

1,62 2 4 16 3,24 6,48

1,72 3 9 81 5,16 1,55

1,78 4 16 2567,12 2,85

y_Э = х_Э=0 х_Э²=0 х_Э⁴= y_Э х_Э= y_Э х_Э²=

= 11,03 =708 =10,6 =68,6

Подставив истинные значения параметров и вернув ось у в исходное положение, имеем

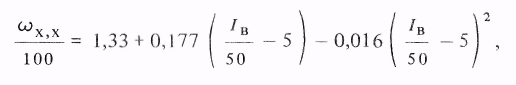
или в окончательном виде

_ХХ = 4,5 + 0,674 I_в  0,6410 ^3 I_в².

Сравнение расчетных данных по полученному выражению с экспериментальным дано в табл. 3.1.

Как видно, модель дает высокую точность совпадения с экспериментом, но так как она строилась для конкретного диапазона изменения входной величины, то при дальнейшем увеличении I_В могут появиться отклонения.

Возможны другие уравнения для моделирования одномерных детерминированных объектов.

Рис. 3.3. Результаты идентификации характеристики двигателя

На рис. 3.3 представлены результаты идентификации универсальной естественной характеристики двигателя постоянного тока последовательного возбуждения. Ее модель имеет вид

у = ₀ + ₁ x + ₂x^1,

или после расчета коэффициентов и замены переменных

_* = 0,84 - 0,078М_* + 0,25 М_*^1 ,

где _* =  /_ном; М_* = М / М _НОМ — относительные значения скорости и момента двигателя.

Обобщенная модель в виде полинома имеет вид

y = (3.19)

где n _i — целое или дробное число любого знака.

Возможны другие виды моделей. Так, если при равных приращениях х_э величина у_э растет примерно в геометрической прогрессии следует применять модели вида

y = b^x , y =  e^bx , y =  sin и др. (3.20)

О целесообразности свидетельствует также линейный характер зависимости между x_Э и lg y_Э , так как из (3.20)

lg y_Э = lg + x _Э lg b

Во всех случаях для определения коэффициентов применяется метод минимума суммы квадратов отклонений.