3.2.2. Модели многосвязных систем

Для современных АСУ ТП характерно объединение в единую систему отдельных приводов и механизмов и даже объединение сложных технологических агрегатов в комплексно-автоматизированные технологические линии, гибкие автоматизированные производства. Примерами первых могут служить станки с ЧПУ, отрабатывающие при обработке детали сложные траектории и обеспечивающие оптимальный режим резания; примерами вторых — технологические линии прокатного производства. Основной особенностью таких систем является невозможность рассмотрения их как механической совокупности отдельных механизмов. Это обусловлено взаимосвязью и взаимовлиянием друг на друга управляемых технологических параметров.

Для обеспечения требуемого качества продукции необходимо одновременно управлять многими взаимосвязанными переменными (технологическими параметрами) путем непрерывного воздействия на различные исполнительные механизмы. В подобных системах изменение одного управляющего или возмущающего воздействия вызывает изменение нескольких управляемых переменных и наоборот - каждая управляемая переменная зависит от нескольких управляющих воздействий. Многосвязными являются большинство систем, у которых есть несколько возможностей управлять одним объектом, подверженным обычно нескольким внешним воздействиям. Подобные системы называют также многоканальными или многомерными.

В многоканальных системах в отличие от одноканальных входные воздействия и выходы объекта в каждый момент времени описываются как многомерные векторы, а сам объект — оператором А, преобразующим вектор входных воздействий X в вектор выходных переменных Y:

(3-4)

В этом случае можно говорить об аналогии между оператором А и передаточной функцией в одноканальных системах. В многокаиальных системах решаются те же задачи, что и в одноканальных, т.е. стабилизация, программное и следящее управление, оптимизация. Здесь также решается вопрос об устойчивости системы, качестве ее динамики. Представляя систему многомерной, необходимо уметь путем структурных преобразований упрощать внутреннюю структуру сложной системы, соединять eе с другими системами и т.д. Самостоятельной задачей является получение и представление формализованных моделей таких систем.

Основным физическим принципом, положенным в основу аналитических методов получения моделей многомерных объектов, является метод универсальных уравнений.

Записав уравнения по типу (3.2), получим, например, для установившегося режима трехсвязной линейной системы уравнения вида

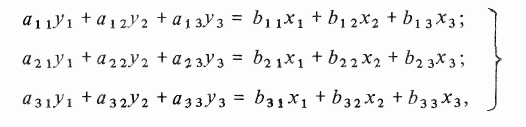(3.5)

где x₁, х₂, х₃ — входные, a y₁ у₂, y₃ — выходные переменные;_ij, b_ij; — коэффициенты — вещественные числа, которые могут принимать также и нулевые значения.

При записи уравнений динамики структура системы уравнений будет аналогичной (3.5), но вместо y_j и х_i будут фигурировать временные функции x_i (t) и y_j (t) или их операторные изображения x_i(p) и y_j(р) а вместо коэффициентов _ij, b_ij— операторные полиномы.

После решения системы уравнений (3.5) или ее динамического аналога она принимает вид

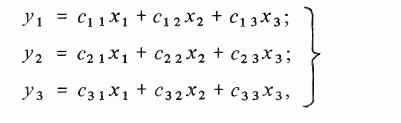(3.6)

где c_ij- вещественный коэффициент для уравнений статики или передаточная функция для уравнений динамики.

Модель системы в виде уравнений (3.5) или (3.6) может быть определена любой внутренней структурой, т.е. связи между каналами могут быть обусловлены непосредственным взаимодействием переменных, прямыми связями входа с различными выходами и обратными связями от выходов к входам. На рис. 3.1 приведена система, обладающая указанными свойствами.Эту систему можно описать следующими уравнениями:

-

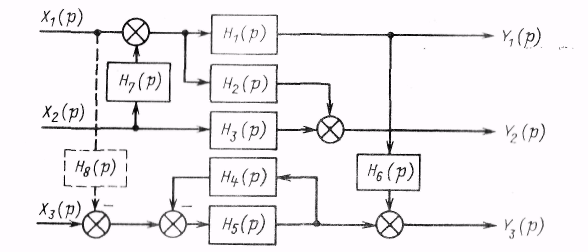
Рис. 3.1. Пример трехсвязной структуры

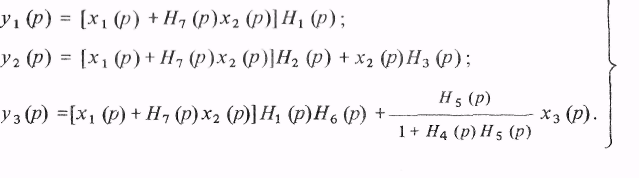
(3-7)

После преобразований система (3.7) принимает вид, аналогичный (3.6):

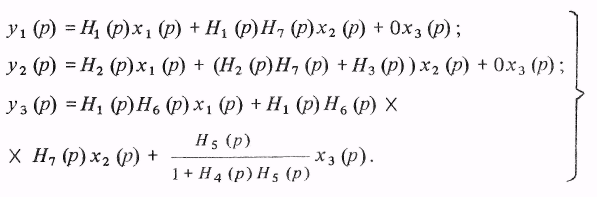(3.8) Как видно из изложенного, даже для относительно простой системы запись формальной модели получается весьма громоздкой. После приведения ее к виду (3.6) решать систему обычным способом становится сложно. С увеличением числа входов и выходов задача еще более усложняется.

Для получения более компактных и унифицированных форм представления моделей многомерных систем применяется матричная форма записи переменных и операторов преобразования.

Например, система (3.5) в матричной форме может быть представлена в виде

AY = ВХ, (3.9)

где X, Y-матрицы входных и выходных переменных; А, В - матрицы преобразований.

Система (3.6) принимает вид

Y = СХ. (3.10)

Под матрицами в данном случае понимается упорядоченная, т.е. выполненная по определенному правилу, табличная форма записи цифр, буквенных коэффициентов или передаточных функций и полиномов. Так, в (3.10) матрицы имеют вид

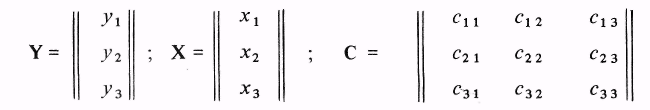
Главное преимущество матричной формы записи заключается в том, что, составляя матрицы по определенным правилам, можно трансформировать в матричную форму не только запись переменных, но и операции над ними.

Использование матричного представления объекта весьма эффективно при анализе и синтезе системы по динамическим показателям. Одним из наиболее современных методов анализа динамики многомерных систем является метод пространства состояний. Под переменными состояния и образуемым ими пространством состояний понимается совокупность величин, позволяющих по известным входным сигналам для t  t₀ определить выходные сигналы для t > t₀.

В качестве переменных состояния могут приниматься как выходные переменные, так и их производные. Так, для одномерной системы, описываемой дифференциальным уравнением n-го порядка, переменными состояния будут значения у и (n - 1) производных в момент t = 0, позволяющие в дальнейшем при решении дифференциального уравнения классическим методом определить постоянные интегрирования.

В качестве примера идентификации многомерной системы рассмотрим испытательный стенд.

• Пример. Стенд, предназначенный для испытаний объемных гидроприводов, оборудован нагрузочным устройством Н в виде машины постоянного тока, связанной через генератор НГ и синхронный двигатель СД с сетью переменного тока для рекуперации энергии нагружения (рис. 3.2, а).

Нагрузочное устройство должно обеспечивать возможность задания нагрузок гидроприводу в широком диапазоне и поддержания их заданных значений. Изменение скорости гидродвигателя (гидромотора) ГМ осуществляется изменением производительности питающего гидронасоса ГН.

+

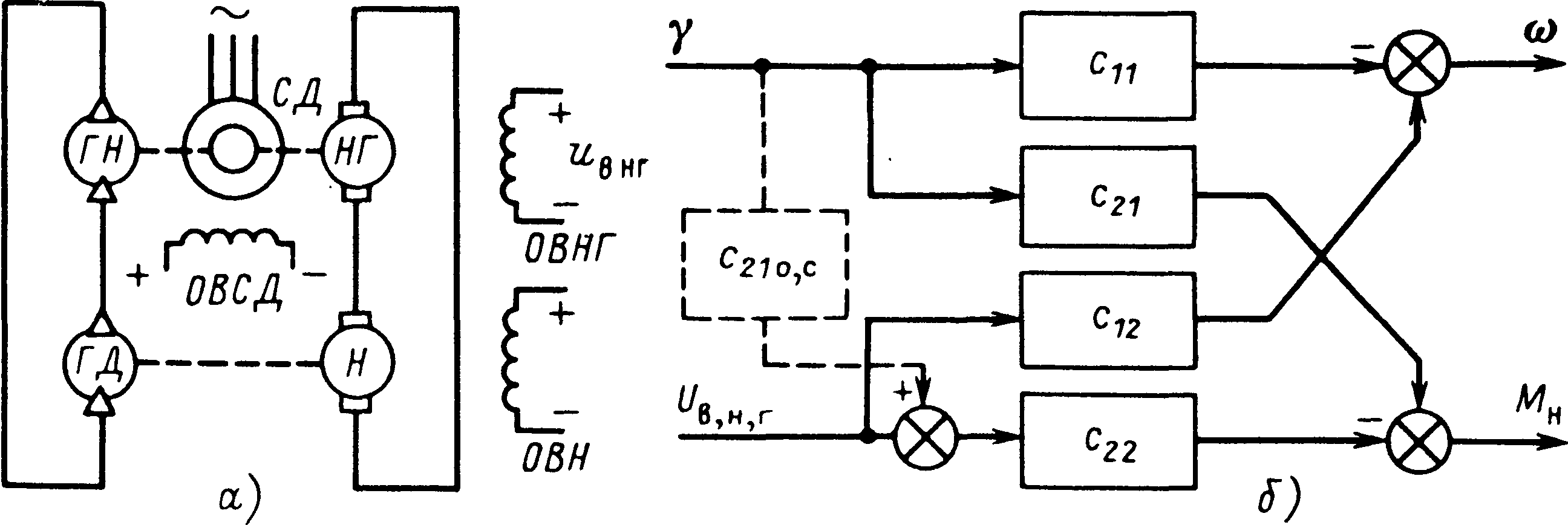
Рис.3.2. Стенд для испытания гидроприводов:

а — схема силового контура; б — эквивалентная структурная схема системы управления

Требуется синтезировать систему управления нагрузкой, инвариантную по угловой скорости.

Исходя из баланса расхода жидкости в контуре ГН → ГМ, уравнений электрического равновесия цепи НГ → Н и механического равновесия, можно записать уравнение системы в операторной форме:

;

;

где М_ГД, М_Н — операторные изображения моментов, развиваемых гидродвигателем и нагружателем; c_j - изображение угловой скорости; Т_ГП,Т_Я — постоянная времени гидропривода, обусловленная сжимаемостью жидкости, и электромагнитная постоянная якорной цепи; с_у — коэффициент, определяющий утечку рабочей жидкости; q_Д — коэффициент пропорциональности между угловой скоростью и расходом жидкости гидродвигателя; k_Q — коэффициент передачи гидронасоса, связывающий его производительность с углом наклона блока поршней 7 (входное управляющее воздействие); k_Н.Г - коэффициент передачи нагрузочного генератора; с - коэффициент двигателя нагружателя; J_Σ, ΔМ_Σ — суммарный момент инерции и момент потерь на трение в силовом контуре стенда;

U_ВНГ- изображение напряжения возбуждения НГ.

Получена система уравнений трехсвязной системы с двумя управляющими входными воздействиями γ и U_ВНГ одним возмущающим ΔМ_Σ и тремя управляемыми М_ГД, М_Н и ω координатами. В ней можно обеспечить однозначное управление лишь двумя выходными переменными, в качестве которых принимаем М_Н и ω, а М_ГД определяем как зависящую от них. Исключив М_ГД и приняв ΔМ_Σ = 0, получим систему уравнений, описывающих стенд как двухканальную систему:

С_у(Т_ГП р + 1)M_Н + (J_Σ С_уТ_ГП р + 1)р + q_m)ω = k_Qγγ

(T_Яр + 1)М_Н + сω = k_НГU_ВНГ

или, введя сокращенные обозначения коэффициентов,

_α11М_Н +α₁₂ω = b₁γ;

α₂₁М_Н + α₂₂ω = b₂U_ВНГ;

Разрешив уравнения относительно ω и М_Н, получим

;

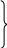; (3.11)

или в матричной форме

ω c₁₁ c₁₂ γ

М_Н = c₂₁ c₂₂ U_ВНГ (3.12)

где c_ij, — передаточные функции для ω и М_Н по управляющим воздействиям.

Как видно из (3.11), как угловая скорость, так и момент нагрузки зависят от двух управляющих воздействий (рис. 4.1, б). Зависимость ω от γ отражает действие на угловую скорость изменения угла наклона блока поршней гидронасоса, а зависимость от U_ВНГ— действия на ω момента нагрузки на валу гидромотора.

Во втором уравнении зависимость момента М_Н от своего задания U_ВНГ необходима, а зависимость его от  либо вообще должна быть устранена, либо должна формироваться как функция ω по соответствующему закону. Так как при испытаниях гидропривода нужна имитация нагрузки, не зависящей от скорости(система инвариантная по скорости), то следует автономизировать канал управления нагрузкой. В управляющее воздействие этого канала введем сигнал, компенсирующий составляющую с₂₁ γ (рис. 3.1, б, штриховые линии), т.е.

с₂₁γ - с₂₂(U_внг + с_21ос γ) = М_Н

где с_21ос - передаточная функция обратной связи, компенсирующей естественное действие γ на М_Н. Тогда

М_Н = (с₂₁ - с₂₂с_21ос)γ + с₂₂U_ВНГ

Чтобы исключить влияние γ полагаем коэффициент при этой координате равным нулю, откуда

с_21ос ⁼ с₂₁/ с₂₂

Раскрывая значение с₂₁ и с₂₂, получаем

(3.13.)

и, обозначая

;

окончательно имеем

(3.14)

Следовательно, для автономизации канала управления нагрузкой, т.е. независимости нагрузки от задания по скорости, надо на его вход подать сигнал задания γ через звено второго порядка с параметрами K_ОС, Т_ГП, Т_ОС.