Xlabel('X')

ylabel('y(x)')

Решаем пример 13a

Подынтегральная функция: F=x^2+y^2+Dy^2

Граничные условия: y(-1)=1; y(1)=2 fi0 =

3/2+1/2*x

fi1 =

sin(1/2*pi*(x+1))

fi2 =

sin(pi*(x+1))

yritz =

3/2+1/2*x+a1*sin(1/2*pi*(x+1))+a2*sin(pi*(x+1))

Jritz =

(1/4*a1^2+a2^2)*pi^2+35/6+a2^2+a1^2+(12*a1-2*a2)/pi

-0.55080426575187

a2r =

0.02928440396155

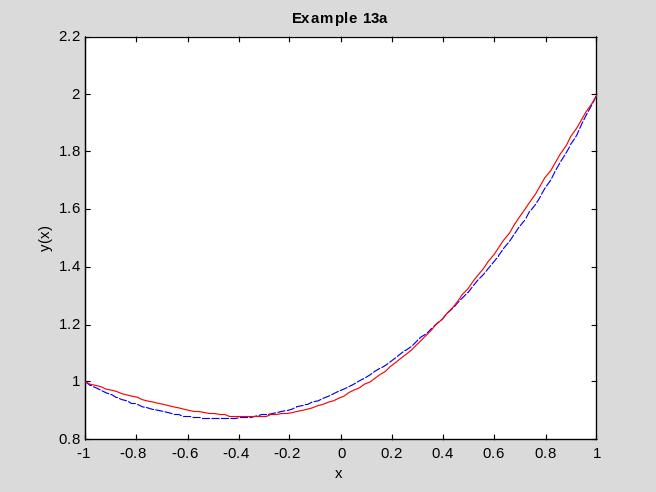
Ответ. Решение задачи методом Ритца имеет вид

. (13.0)

График этого решения показан на рис.13.1 сплошной красной линией. Штриховая синяя линия – аналитическое решение.

2. Пример 13b

Решить методом Ритца пример 4. Взять в качестве базисных функций одну и две полуволны синуса по обеим координатам. Построить график. Сравнить с решением МКР 12b и МКЭ 4. Удачно ли подобраны базисные функции?

Будем искать решение в виде

, (13.0)

где ₀(x,y) – функция, удовлетворяющая граничным условиям, а ₁₁(x,y), ₂₁(x,y), ₁₂(x,y) и ₂₂(x,y) – базисные функции, удовлетворяющие однородным (нулевым) граничным условиям. В качестве ₀(x,y) возьмём заданное граничное условие:

. (13.0)

Базисные функции _ik(x,y) – это функции, имеющие i полуволн синуса в направлении x и k в направлении y.

(13.0)

Используем программы для решения примеров 13a и 4. Описываем символические константы и вводим исходные данные.

clear all

format long

disp('Решаем пример 13b')

n = 20; % число точек для построния графика

syms x y z Dzx Dzy a11 a21 a12 a22 % переменные

F = Dzx^2-2*Dzy^2+2*y*z*(sin(pi*x)+x/5); % подынтегральная функция

zc = x/10+y^2/50; % функция граничных условий

x1 = 0;

x2 = 1;

y1 = 0;

y2 = 2;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничное условие на контуре: z=%s\n',char(zc))

fprintf('Область: %d<=x<=%d; %d<=y<=%d\n',x1,x2,y1,y2)

x1s = sym(x1);

x2s = sym(x2);

y1s = sym(y1);

y2s = sym(y2);

fi11 = sin(pi*(x-x1s)/(x2s-x1s))*sin(pi*(y-y1s)/(y2s-y1s))

fi21 = sin(2*pi*(x-x1s)/(x2s-x1s))*sin(pi*(y-y1s)/(y2s-y1s))

fi12 = sin(pi*(x-x1s)/(x2s-x1s))*sin(2*pi*(y-y1s)/(y2s-y1s))

fi22 = sin(2*pi*(x-x1s)/(x2s-x1s))*sin(2*pi*(y-y1s)/(y2s-y1s))

zritz = zc+a11*fi11+a21*fi21+a12*fi12+a22*fi22

dzritzdx = diff(zritz,x);

dzritzdy = diff(zritz,y);

x1s = sym(x1);

x2s = sym(x2);

y1s = sym(y1);

y2s = sym(y2);

fi11 = sin(pi*(x-x1s)/(x2s-x1s))*sin(pi*(y-y1s)/(y2s-y1s))

fi21 = sin(2*pi*(x-x1s)/(x2s-x1s))*sin(pi*(y-y1s)/(y2s-y1s))

fi12 = sin(pi*(x-x1s)/(x2s-x1s))*sin(2*pi*(y-y1s)/(y2s-y1s))

fi22 = sin(2*pi*(x-x1s)/(x2s-x1s))*sin(2*pi*(y-y1s)/(y2s-y1s))

zritz = zc+a11*fi11+a21*fi21+a12*fi12+a22*fi22

dzritzdx = diff(zritz,x);

dzritzdy = diff(zritz,y);

eq11 = diff(Jritz,a11);

eq21 = diff(Jritz,a21);

eq12 = diff(Jritz,a12);

eq22 = diff(Jritz,a22);

eq11 = [char(eq11),'=0'];

eq21 = [char(eq21),'=0'];

eq12 = [char(eq12),'=0'];

eq22 = [char(eq22),'=0'];

S = solve(eq11,eq21,eq12,eq22,a11,a21,a12,a22);

r11 = eval(S.a11)

r21 = eval(S.a21)

r12 = eval(S.a12)

r22 = eval(S.a22)

[X,Y]=meshgrid(linspace(x1,x2),linspace(y1,y2));

zr = subs ( subs(zritz,{a11,a12,a21,a22},{r11,r12,r21,r22}), {x,y}, {X,Y} );

surfl(X,Y,zr)

title('\bfExample 13b')