Xlabel('X')

ylabel('y')

zlabel('z(x,y)')

v = axis;

da = daspect;

da(1:2) = min(da(1:2));

daspect(da);

axis(v);

colormap(gray) % палитра

Решаем пример 12b

Подынтегральная функция: F=Dzx^2-2*Dzy^2+2*y*z*(sin(pi*x)+1/5*x)

Граничное условие на контуре: z=1/10*x+1/50*y^2

Область: 0<=x<=1; 0<=y<=2

del = 0.05000000000000

nx = 20

ny = 40

dx =1/20

dy =1/20

EqF =

1/4*(ykm1+yk)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(ykm1+yk)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)+1/4*(yk+ykp1)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(yk+ykp1)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)-800*zip1k-1600*zik-800*zim1k+1600*zikp1+1600*zikm1

Текст файла MyEqF.m

function y = MyEqF ( xy, zim1km1, zikm1, zip1km1, zim1k, zik, zip1k, zim1kp1, zikp1, zip1kp1 )

xim1=xy(1); xi=xy(2); xip1=xy(3); ykm1=xy(4); yk=xy(5); ykp1=xy(6);

y=1/4*(ykm1+yk)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(ykm1+yk)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)+1/4*(yk+ykp1)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(yk+ykp1)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)-800*zip1k-1600*zik-800*zim1k+1600*zikp1+1600*zikm1;

neq = 741

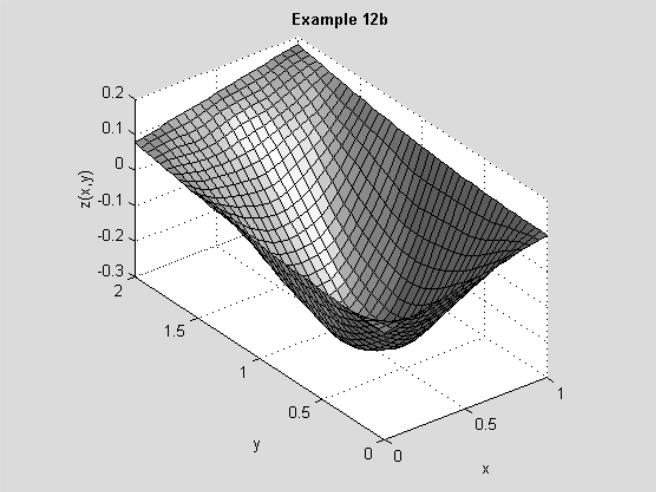
Рис. 12.6. Решение примера 12b

Ответ. Для сетки 2040 система уравнений МКР вида (12.3) имеет вид

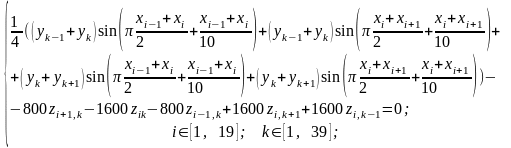(12.0)

при этом входящие в (12.8) величины z при i=1, i=20, k=1, k=40 находятся из граничного условия в соответствующей точке. График экстремальной поверхности показан на рисунке в зоне вывода. Видно, что он очень похож на поверхность, построенной по МКЭ в главе 4.

10. Численные методы 3. Метод Ритца

    1. Краткие теоретические сведения

В методе Ритца решение вариационной задачи ищется в виде линейной комбинации известных, заданных заранее функций (они называются базисными). После подстановки такой линейной комбинации в функционал он становится функцией неизвестных коэффициентов этой комбинации. Коэффициенты подбираются так, чтобы функционал принимал экстремальное значение. Таким образом, вариационная задача сводится к задаче исследования на экстремум функции нескольких переменных.

Линейная комбинация базисных функций должна удовлетворять граничным условиям при любых значениях коэффициентов. Если граничные условия однородные (нулевые), то и базисные функции должны удовлетворять однородным граничным условиям. Если же граничные условия неоднородные, то можно применить следующий приём. Будем искать решение в виде линейной комбинации базисных функций, удовлетворяющих однородным граничным условиям, но прибавим к этой комбинации какую-либо функцию, удовлетворяющую заданным граничным условиям. Коэффициент при этой функции не варьируется, он всегда равен 1. Таким образом, полученная линейная комбинация при любых значениях варьируемых параметров будет удовлетворять заданным граничным условиям.

2. Примеры выполнения заданий

   1. Пример 13a

Решить методом Ритца пример 1a. Взять базисные функции: одну полуволну синуса и две полуволны синуса. Сравнить решение с аналитическим. Построить графики.

Будем искать решение в виде

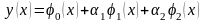, (13.0)

где ₀(x) – любая функция, удовлетворяющая граничным условиям, а ₁(x) и ₂(x) – базисные функции, удовлетворяющие однородным (нулевым) граничным условиям. Выберем ₀(x) в виде прямой, соединяющей граничные точки M₁(x₁,y₁) и M₂(x₂,y₂)

. (13.0)

Базисные функции:

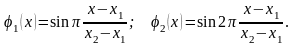(13.0)

Составим программу для этого примера на основе программы для примера 1a. Вводим исходные данные. Решаем пример 1a.

clear all

format long

disp('Решаем пример 13a')

syms x y Dy D2y a1 a2 % описали переменные

F = x^2+y^2+Dy^2; % подынтегральная функция

x1 = -1;

y1 = 1;

x2 = 1;

y2 = 2;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничные условия: y(%d)=%d; y(%d)=%d\n',x1,y1,x2,y2)

dFdy = diff(F,y);

dFdy1 = diff(F,Dy);

d_dFdy1_dx = diff(dFdy1,x);

d_dFdy1_dy = diff(dFdy1,y);

d_dFdy1_dy1 = diff(dFdy1,Dy); % d(dF/dy')/dy'

dFy1dx = d_dFdy1_dx + d_dFdy1_dy*Dy + d_dFdy1_dy1*D2y;

Euler = simple(dFdy-dFy1dx);

deqEuler = [ char(Euler) '=0' ]; % составили уравнение

Sol = dsolve(deqEuler,'x'); % решаем уравнение Эйлера

if length(Sol)~=1 %решений нет или более одного

error('Нет решений или более одного решения!');

end

SolLeft = subs(Sol,x,sym(x1));

SolRight = subs(Sol,x,sym(x2));

EqLeft = [char(SolLeft) '=' char(sym(y1))];

EqRight = [char(SolRight) '=' char(sym(y2))];

Con = solve(EqLeft,EqRight); % решаем систему

C1 = Con.C1;

C2 = Con.C2;

Sol1a = vpa(eval(Sol),14);

xpl = linspace(x1,x2);

y1a = subs(Sol1a,x,xpl);

x1s = sym(x1);

x2s = sym(x2);

y1s = sym(y1);

y2s = sym(y2);

fi0 = y1s+(y2s-y1s)*(x-x1s)/(x2s-x1s)

fi1 = sin(pi*(x-x1s)/(x2s-x1s))

fi2 = sin(2*pi*(x-x1s)/(x2s-x1s))

yritz = fi0+a1*fi1+a2*fi2

dyritzdx = diff(yritz,x);

Fritz = simple(subs(F,{y,Dy},{yritz,dyritzdx}));

Jritz = simple(int(Fritz,x,x1s,x2s))

eq1 = diff(Jritz,a1);

eq2 = diff(Jritz,a2);

eq1 = [char(eq1),'=0'];

eq2 = [char(eq2),'=0'];

S = solve(eq1,eq2,a1,a2); % решаем относительно a1, a2

a1r = eval(S.a1)

a2r = eval(S.a2)

yr=subs(subs(yritz,{a1,a2},{a1r,a2r}),x,xpl);

plot(xpl,y1a,'--b',xpl,yr,'-r')

title('\bfExample 13a')