Xlabel('X')

ylabel('y(x)')

zlabel('z(x)')

View(205,30)

grid on

box on

Решаем пример 11b

Подынтегральная функция: F=Dy^2+Dz^2+2*y*z

Граничные условия слева: y(-2)=1; z(-2)=0

Граничные условия справа: y(2)=0; z(2)=2

Текст файла MyRightPart.m

function dydx = MyRightPart(x,y)

dydx=zeros(4,1);

dydx(1)=y(2);

dydx(2)=(y(3));

dydx(3)=y(4);

dydx(4)=(y(1));

b = 13.32736606398895

11.98099902570117

A = 13.26662430099436 14.02342479230629

14.02342479230629 13.26662430099436

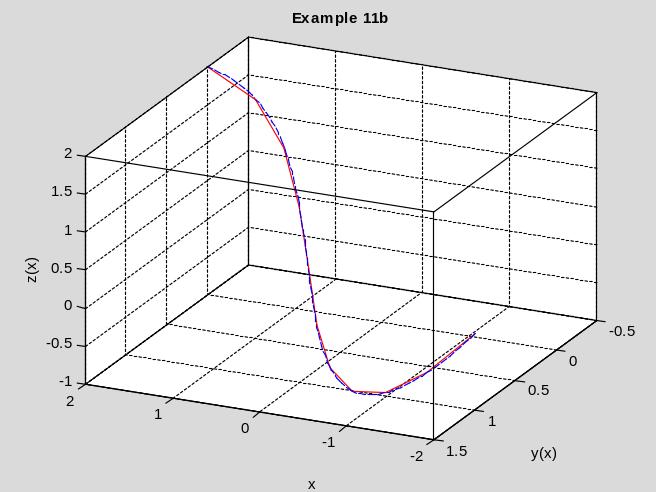
Рис. 11.3. Решение примера 11b

Ответ. График экстремали показан на рис.11.3 сплошной красной линией. Он практически сливается с решением примера 2, которое показано штриховой синей линией. Неизвестные начальные условия: y(x₁)0.42582; z(x₁)1.35320.

3. Пример 11c

Решить методом начальных параметров пример 3. Сравнить решение с аналитическим. Построить графики.

clear all

format long

disp('Решаем пример 11c')

nnp = 10;

syms x y Dy D2y D3y D4y % описали переменные

F = D2y^2-2*Dy^2+4*y*Dy+y^2-2*y*sin(x);

x1 = -1;

y1 = 1;

Dy1 = -1;

x2 = 1;

y2 = 2;

Dy2 = 1;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничные условия слева: y(%d)=%d; y''(%d)=%d\n',x1,y1,x1,Dy1)

fprintf('Граничные условия справа: y(%d)=%d; y''(%d)=%d\n',x2,y2,x2,Dy2)

dFdy = diff(F,y);

dFdy1 = diff(F,Dy);

dFdy2 = diff(F,D2y); % dF/dy''

d_dFdy1_dx = diff(dFdy1,x); % d(dF/dy')/dx

d_dFdy1_dy = diff(dFdy1,y); % d(dF/dy')/dy

d_dFdy1_dy1 = diff(dFdy1,Dy); % d(dF/dy')/dy'

d_dFdy1_dy2 = diff(dFdy1,D2y); % d(dF/dy')/dy''

dFy1dx = d_dFdy1_dx + d_dFdy1_dy * Dy + d_dFdy1_dy1 * D2y + d_dFdy1_dy2*D3y;

d_dFdy2_dx = diff(dFdy2,x); % d(dF/dy'')/dx

d_dFdy2_dy = diff(dFdy2,y); % d(dF/dy'')/dy

d_dFdy2_dy1 = diff(dFdy2,Dy); % d(dF/dy'')/dy'

d_dFdy2_dy2 = diff(dFdy2,D2y); % d(dF/dy'')/dy''

dFy2dx = d_dFdy2_dx + d_dFdy2_dy * Dy + d_dFdy2_dy1 * D2y + d_dFdy2_dy2 * D3y;

d_dFdy2dx_dx = diff(dFy2dx,x); % d((dFy'')/dx)/dx

d_dFdy2dx_dy = diff(dFy2dx,y); % d((dFy'')/dx)/dy

d_dFdy2dx_dy1 = diff(dFy2dx,Dy); % d((dFy'')/dx)/dy'

d_dFdy2dx_dy2 = diff(dFy2dx,D2y); % d((dFy'')/dx)/dy''

d_dFdy2dx_dy3 = diff(dFy2dx,D3y); % d((dFy'')/dx)/dy'''

d2Fy2dx2 = d_dFdy2dx_dx + d_dFdy2dx_dy * Dy + d_dFdy2dx_dy1 * D2y + d_dFdy2dx_dy2 * D3y + d_dFdy2dx_dy3 * D4y;

Euler = simple(dFdy-dFy1dx+d2Fy2dx2);

deqEuler = [char(Euler) '=0']; % составили уравнение

Sol = dsolve ( deqEuler, 'x' );

if length(Sol)~=1 % решений нет или более одного

error('Нет решений или более одного решения!');

end

dydx = diff(Sol,x); % нашли производную

slY = subs(Sol,x,sym(x1));

slDY = subs(dydx,x,sym(x1));

srY = subs(Sol,x,sym(x2));

srDY = subs(dydx,x,sym(x2));

elY = [char(vpa(slY,14)) '=' char(sym(y1))];

elDY = [char(vpa(slDY,14)) '=' char(sym(Dy1))];

erY = [char(vpa(srY,14)) '=' char(sym(y2))];

erDY = [char(vpa(srDY,14)) '=' char(sym(Dy2))];

Con = solve(elY,elDY,erY,erDY);

C1 = Con.C1;

C2 = Con.C2;

C3 = Con.C3;

C4=Con.C4;

Sol3 = vpa(eval(Sol),14); % подставляем C1-C4;

xpl = linspace(x1,x2);

y3 = subs(Sol3,x,xpl);

f4 = solve(deqEuler,D4y); % находим D4y

f4 = subs(f4,{y,Dy,D2y,D3y},{sym('y(1)'),sym('y(2)'),sym('y(3)'),sym('y(4)')});

rp{1} = 'function dydx = MyRightPart(x,y)';

rp{2} = 'dydx=zeros(4,1);';

rp{3} = 'dydx(1)=y(2);';

rp{4} = 'dydx(2)=y(3);';

rp{5} = 'dydx(3)=y(4);';

rp{6} = [ 'dydx(4)=' char(f4) ';' ];

disp('Текст файла MyRightPart.m')

fprintf('%s\n',rp{:});

fid = fopen ( 'C:\Iglin\Matlab\MyRightPart.m', 'w' );

fprintf(fid,'%s\n',rp{:});

fclose(fid); % закрываем файл

xr = linspace(x1,x2,nnp+1); % точки для численного решения

A = zeros(2,2);

b = zeros(2,1);

y0 = [y1;Dy1;0;0]; % начальные условия (0,0)

[xx,YY] = ode45('MyRightPart',xr,y0); % решаем СДУ

b = YY(nnp+1,[1 2])' - [y2;Dy2] % правые части

y0 = [y1;Dy1;1;0]; % начальные условия (1,0)

[xx,YY] = ode45('MyRightPart',xr,y0); % решаем СДУ

A(:,1) = YY(nnp+1,[1 2])'-[y2;Dy2]-b; % 1-й столбец матрицы A

y0 = [y1;Dy1;0;1]; % начальные условия (0,1)

[xx,YY] = ode45('MyRightPart',xr,y0); % решаем СДУ

A(:,2) = YY(nnp+1,[1 2])'-[y2;Dy2]-b % 2-й столбец матрицы A

yz0 = -A\b; % нашли начальные условия

y0 = [y1;Dy1;yz0] % истинные начальные условия

[xx,YY] = ode45('MyRightPart',xr,y0); % решаем

plot(xpl,y3,'--b',xr,YY(:,1),'-r' )

title ( '\bfExample 11c' ) % заголовок