Тема 6. Выборочное наблюдение

Тема «Выборочное наблюдение» является одной из центральных в курсе теории статистики. Выборочное наблюдение тесно связано с курсами математической статистики и теории вероятностей.

Часть единиц отобранных для наблюдений принято называть выборкой, а всю совокупность единиц из которых производится отбор – генеральной совокупностью. Качество результатов выборочного наблюдения зависит от того, на сколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна. Чтобы обеспечить репрезентативность выборки, необходимо соблюдать принцип случайности отбора единиц.

Особенности обследуемых объектов определяют 2 метода отбора единиц в выборочную совокупность – повторный и бесповторный. При повторном отборе каждая попавшая в выборку единица возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. Бесповторный отбор означает, что каждая отобранная единица не возвращается в генеральную совокупность и не может подвергнуться вторичной регистрации, а потому для остальных единиц вероятность попасть в выборку увеличивается. Понятно, что бесповторный отбор дает более точные результаты.

Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Расчёт ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.

Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным об успеваемости студентов.

Оценка	Число студентов, чел.
	Генеральная совокупность	Первая выборка	Вторая выборка
2	100	9	12
3	300	27	29
4	520	54	52
5	80	10	7
Итого	1000	100	100

Средний балл по генеральной совокупности

по первой выборке

по второй выборке .

Доля студентов, получивших «4» и «5»:

по генеральной совокупности

по первой выборке

по второй выборке

Как видно из расчетов, выборочная средняя и выборочная доля являются случайными величинами и могут принимать различные значения, в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок:

Для средней

Для доли

В этих формулах и являются характеристиками генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности на основании закона больших чисел.

При бесповторном отборе подкоренное выражение умножается на величину ( ), которая всегда меньше единицы, поэтому величина средней ошибки выборки при бесповторном отборе оказывается меньше, чем при повторном. В тех случаях, когда доля выборки незначительна и множитель ( ) близок к единице, поправкой можно пренебречь. Для решения практических задач кроме средней пользуются предельной ошибкой выборки, которая связана с гарантирующим её уровнем вероятности. Уровень вероятности определяет величина нормированного отклонения , и наоборот. Значение даются в таблицах нормального распределения вероятностей. Чаще всего используют следующие сочетания:

	0,683
	0,866
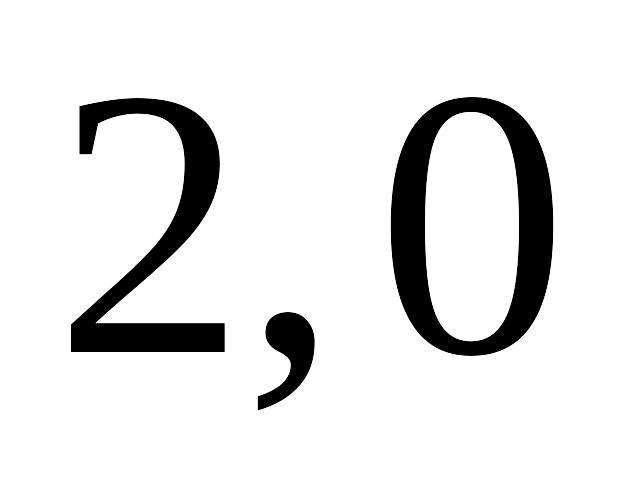
	0,954
	0,988
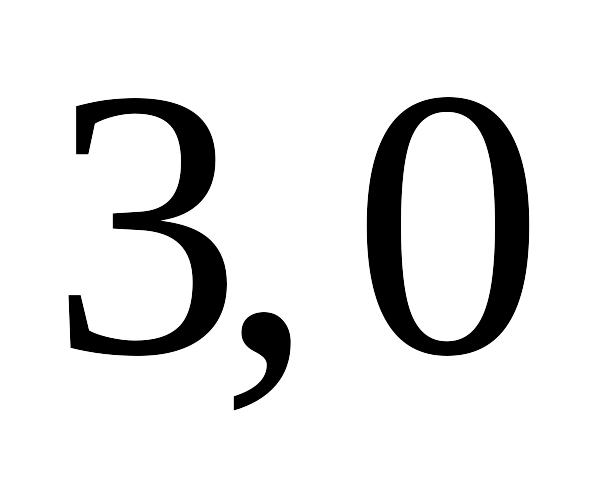
	0,997
	0,999

Предельные ошибки выборки ( ) определяются по формулам

Метод отбора	Для средней	Для доли
Повторный
Бесповторный

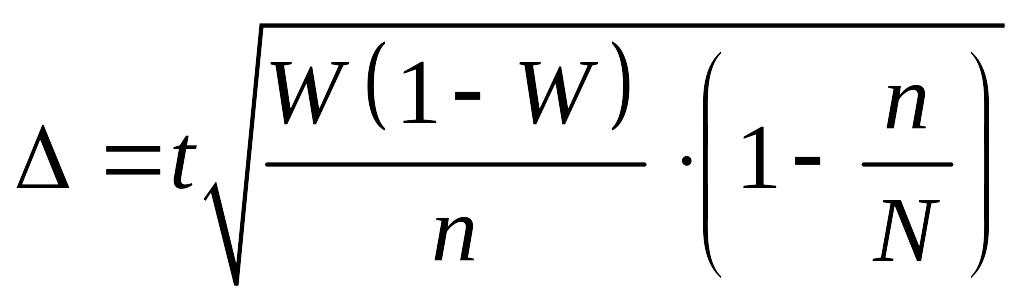
После исчисления предельных ошибок выборки находят доверительные интервалы для генеральных показателей. Для это ( ), для это ( ).

Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остаётся тот минимальный объём выборки, который должен обеспечить требуемую точность. Формулы для определения численности выборки ( ) следует из формул предельных ошибок выборки.

Метод отбора	Для средней	Для доли
Повторный
Бесповторный

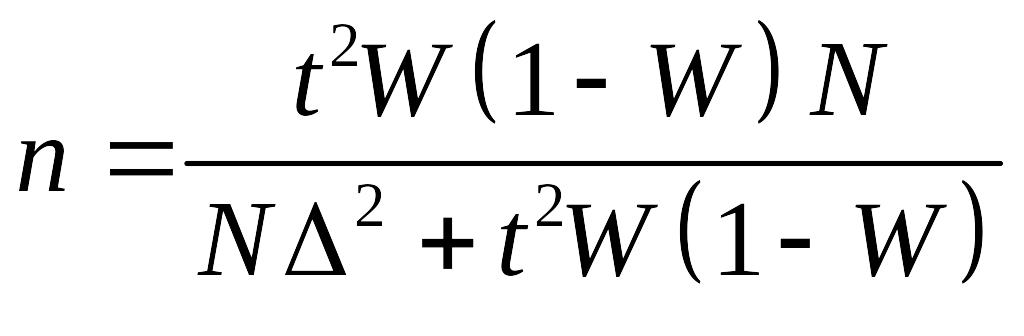
Значения и определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. Вариация ( ) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Обычно определяют из предыдущих исследований.

Пример 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборке было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.

Решение. Рассчитываем сначала предельную ошибку выборки.

Так, при ,

.

Определим пределы генеральной средней:

.